유한 직선 도선 으로부터 자계

 

 

이번 편은 비오 사바르 법칙 4편입니다.

 

이전 편을 보지 않으신 분들께서는 

https://pilgigo.tistory.com/entry/%EC%9B%90%ED%98%95-%EB%8F%84%EC%84%A0-%EC%A4%91%EC%8B%AC-%EC%9C%84%EC%97%90%EC%84%9C%EC%9D%98-%EC%9E%90%EA%B3%84

원형 도선 중심 위에서의 자계

여기를 참고해 주세요.

 

이번 편을 보기 위해서는 비오 사바르 법칙에 대한 공부가 되어 있어야 합니다.

비오 사바르 법칙은

https://pilgigo.tistory.com/entry/%EB%B9%84%EC%98%A4-%EC%82%AC%EB%B0%94%EB%A5%B4-%EB%B2%95%EC%B9%99

비오 사바르 법칙

여기를 참고해 주세요.^^

 

 

그럼 시작하겠습니다.

 

 

다음과 같이 전류가 흐르는 유한 직선 도선이 있다고 하자.

도선이 어디에 있냐면

 빨간색 네모로 표시된 부분만 도선이다.

 

구하고자 하는 자계의 방향은 들어가는 방향임을 알 수 있다.

구하고자 하는 자계의 세기는

그림과 같이 초록색 내모칸 부분으로부터 발생한 자계와

파란색 내모칸 부분으로부터 발생한 자계의 합으로 구할 수 있다.

 

 

먼저 초록색 내모칸 부분으로부터 발생한 자계의 세기부터 구해보자.

 

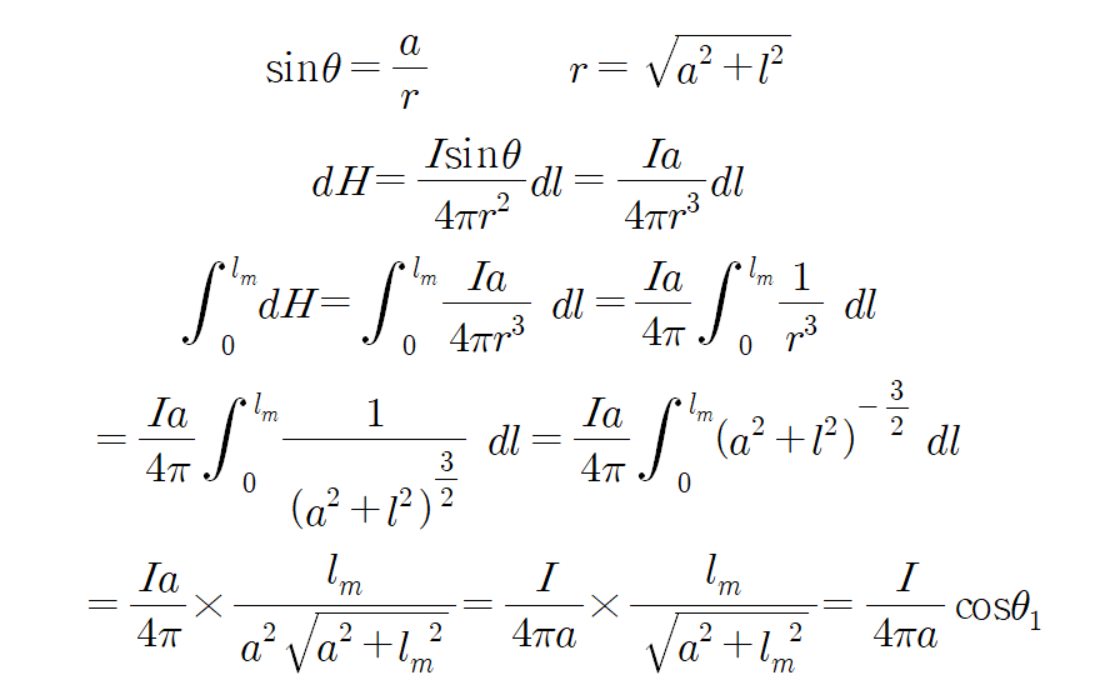
같은 방법으로

파란색 내모칸 부분으로부터의 자계의 세기를 구하면

이렇게 되므로

이 둘을 합하면 우리가 알고자 한 공식이 나온다.

5편에 계속

https://pilgigo.tistory.com/entry/%EB%AC%B4%ED%95%9C-%EC%A7%81%EC%84%A0-%EB%8F%84%EC%84%A0%EC%9C%BC%EB%A1%9C%EB%B6%80%ED%84%B0%EC%9D%98-%EC%9E%90%EA%B3%84

무한 직선 도선으로부터의 자계

5편은 여기↑

 

 

https://pilgigo.tistory.com/entry/%ED%99%98%EC%83%81-%EC%86%94%EB%A0%88%EB%85%B8%EC%9D%B4%EB%93%9C%EC%9D%98-%EC%9E%90%EA%B3%84

환상 솔레노이드의 자계