2022. 3. 7. 12:06ㆍ물리
이번 편에는 인덕터에 대한 전자기학적 해석을 해볼 겁니다.
그럼 시작하겠습니다.
인덕터란.
다음과 같은 모양을 하고 있는 도선이다.

이 인덕터에 전류가 흐르면 어떻게 될까?
우리는 도선에 전류가 흐르면 주변에 자계가 생긴다고
비오 사바르 법칙을 통해 알아보았다.
비오 사바르 법칙에 대한 것은
https://pilgigo.tistory.com/entry/%EB%B9%84%EC%98%A4-%EC%82%AC%EB%B0%94%EB%A5%B4-%EB%B2%95%EC%B9%99
비오 사바르 법칙
비오 사바르 법칙에 대해 알아보자. 다음과 같이 도선에 전류가 흐르고 있다 하자. 이때 도선 주위의 임의의 점에서 자계가 있을거다. 전류가 흐르는 도선 주위에는 자계가 생긴다. (벡터 외적
pilgigo.tistory.com
여기를 참고해 주세요.^^
따라서 인덕터에 전류가 흐르면

다음과 같이 자계가 발생할 것이다.

이렇게 인덕터로부터 발생한 자계는
보다시피
인덕터 내부 공간에도 있고
인덕터 외부 공간에도 있다.
즉. 모든 위치에 자계 벡터가 있다.
(위 그림에서는 표현하지 않았지만, 인덕터로부터 생긴 자계는 인덕터와 아무리 멀리 있어도 미약하게나마 존재한다.)
모든 위치에서 존재하는 각각의 자계 벡터들은
비오 사바르 법칙을 이용해서
그 크기를 각각 하나하나 계산할 수 있다.
물론 인덕터의 형태 구조 특성상 매우 난해한 계산과정이 필요할 거다.
(거의 불가능에 가까운 난이도이다.)
하지만 계산하지 않고도 확실히 알 수 있는 사실이 있다.
'모든 위치에서 존재하는 각각의 자계 벡터들은,
그 크기가 전류의 크기와 정비례한다'는 사실이다.
비오 사바르 법칙 식을 보면 단번에 납득할 것이다.
자기학에 기본 상식.
자계는 자속 밀도와 정비례한다.
그 비례 상수는 투자율이다.
투자율은 자기적 상호작용을 하는 공간에 무엇으로 채워져 있냐에 따라 변하는 값이다.
자속밀도는 자속 수와 정비례한다.
이는 너무나 자명하므로 설명 생략한다.
정리하자면
인덕터에 흐르는 전류의 크기는, 그로부터 생긴 자계의 크기와 서로 정비례한다.
어떤 위치에서의 자계 벡터 크기 값은, 해당 위치의 자속 밀도와 서로 정비례한다.
어떤 공간에서의 자속 밀도 값은, 해당 공간의 자속 수와 서로 정비례한다.
따라서 인덕터에 흐르는 전류는,
그로부터 생긴 모든 자속 수와
서로 정비례한다.
인덕터에 흐르는 전류값이 결정됨에 따라,
인덕터에서 발생한 자속 수가 결정되는
함수가 있다고 하자.
(전류-자속 수) 함수는 일차함수(직선 그래프)이다.
이는 기울기가 항상 상수임을 뜻한다.

이 내용을 꼭 기억하고 넘어가자.
다시 처음 이야기로 돌아가서
인덕터에 전류를 흘러 보내니

다음과 같이 자속 수가 여러개 발생하였다.

즉. 없던 자속 수가 갑자기 생겨난 것이고,
이는 단위 시간 동안 자속 수 변화가 있었다는 것을 뜻한다.
코일 주변에서 시간에 따른 자속 수 변화가 생기면,
패러대이 법칙에 의해 유도 기전력(전압)이 발생한다.
이는 수식으로 다음과 같이 표현 가능하다.

여기서 합성함수 미분공식에 의해 다음과 같이 계산 가능하다.

여기서 새로운 개념을 정의해 보자.

인덕터의 모양을 변형하거나 감은수를 변화시키지 않는 이상 인덕턴스는 항상 상수이다.

정리해서

이 공식을 외우기 쉽게
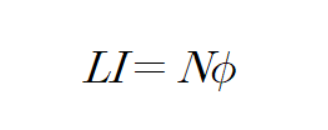
라고 쓰자.
'물리' 카테고리의 다른 글
| 환상 솔레노이드의 상호 인덕턴스 (4) | 2022.03.16 |
|---|---|
| 운동에너지(미적분으로 해석) (0) | 2022.03.09 |
| 무한 직선 도선으로부터의 자계 (0) | 2022.02.25 |
| 유한 직선 도선 으로부터 자계 (0) | 2022.02.24 |
| 원형 도선 중심 위에서의 자계 (0) | 2022.02.21 |