오각도선 중심에서의 자계

 

 

이번 편은 오각도선 중심에서의 자계를 알아볼 겁니다.

이번 편을 공부하기 위해서는 유한 직선 도선으로부터의 자계를 알고 있어야 합니다.

https://pilgigo.tistory.com/entry/%EC%9C%A0%ED%95%9C-%EC%A7%81%EC%84%A0-%EB%8F%84%EC%84%A0-%EC%9C%BC%EB%A1%9C%EB%B6%80%ED%84%B0-%EC%9E%90%EA%B3%84

유한 직선 도선 으로부터 자계

여기를 참고해 주세요. ^^

 

 

그럼 시작하겠습니다.

 

다음과 같은 오각형 도선이 있다고 하자.

이 오각형은 정오각형 이다.

우선 정오각형이라는 도형부터 해석해 보자.

계산의 편이를 위해

라고 하자.

그러므로 다음과 같은 계산을 할 수 있다.

따라서

이므로 정오각형 한변의 길이와 반지름(?)과의 관계식은 다음과 같다.

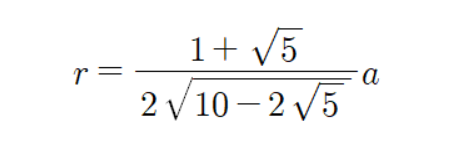
이제 자계를 구해보자.

 

 

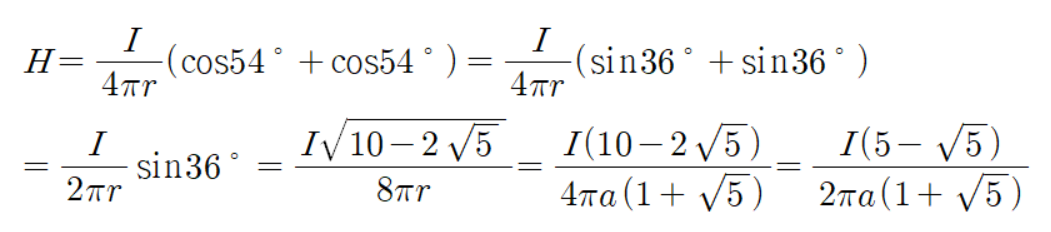
정육각형 도선 중심에서의 자계가 궁금하신 분들께서는

https://pilgigo.tistory.com/entry/%EC%A0%95%EC%9C%A1%EA%B0%81%ED%98%95-%EB%8F%84%EC%84%A0-%EC%A4%91%EC%8B%AC%EC%97%90%EC%84%9C%EC%9D%98-%EC%9E%90%EA%B3%84

정육각형 도선 중심에서의 자계

여기를 참고해 주세요. (훨씬 쉬워요^^)

 

정사각형 도선 중심에서의 자계가 궁금하신 분들께서는

https://pilgigo.tistory.com/entry/%EC%A0%95%EC%82%AC%EA%B0%81%ED%98%95-%EB%8F%84%EC%84%A0-%EC%A4%91%EC%8B%AC%EC%97%90%EC%84%9C%EC%9D%98-%EC%9E%90%EA%B3%84

정사각형 도선 중심에서의 자계

여기를 참고해 주세요. :)

 

정삼각형 도선 중심에서의 자계가 궁금하신 분들께서는

https://pilgigo.tistory.com/entry/%EC%82%BC%EA%B0%81-%EB%8F%84%EC%84%A0-%EC%A4%91%EC%8B%AC%EC%97%90%EC%84%9C%EC%9D%98-%EC%9E%90%EA%B3%84

삼각 도선 중심에서의 자계

여기를 참고해 주세요.

 

원형 도선 중심에서의 자계가 궁금하신 분들께서는

https://pilgigo.tistory.com/entry/%EC%9B%90%ED%98%95-%EB%8F%84%EC%84%A0-%EC%A4%91%EC%8B%AC%EC%97%90%EC%84%9C%EC%9D%98-%EC%9E%90%EA%B3%84

원형 도선 중심에서의 자계

여기를 참고해 주세요. ^^