무한 솔레노이드의 상호 인덕턴스

 

 

이번 편은 무한 솔레노이드의 상호 인덕턴스에 대해 알아볼 겁니다.

 

우선 인덕터에 대해 모르신다면 

https://pilgigo.tistory.com/entry/%EC%9D%B8%EB%8D%95%ED%84%B0%EC%BD%94%EC%9D%BC

인덕터(코일)

여기를 참고해 주세요. :)

 

 

이번 편에 꼭 필요한 수학 개념이 있습니다.

https://pilgigo.tistory.com/entry/%EB%B2%A1%ED%84%B0-%EB%A9%B4%EC%A0%81%EB%B6%84

벡터 면적분

여기를 반드시 보고와 주세요. :)

 

 

 

이번 편을 보기 전 환상 솔레노이드에서의 상호 인덕턴스 편을 먼저 공부하신다면 이해가 더 빠를 것입니다.

https://pilgigo.tistory.com/entry/%ED%99%98%EC%83%81-%EC%86%94%EB%A0%88%EB%85%B8%EC%9D%B4%EB%93%9C%EC%9D%98-%EC%83%81%ED%98%B8-%EC%9D%B8%EB%8D%95%ED%84%B4%EC%8A%A4

환상 솔레노이드의 상호 인덕턴스

여기를 참고해 주세요.^^

 

 

이번 편은 무한 솔레노이드를 해석하는 것이므로

무한 솔레노이드에서의 자계에 대해 미리 공부하시길 바랍니다.

https://pilgigo.tistory.com/entry/%EB%AC%B4%ED%95%9C-%EC%86%94%EB%9E%98%EB%85%B8%EC%9D%B4%EB%93%9C%EC%9D%98-%EC%9E%90%EA%B3%84

무한 솔래노이드의 자계

이는 여기를 참고해 주세요. :)

 

 

그럼 시작하겠습니다.

 

 

다음과 같이 무한 솔레노이드가 있다고 하자.

이러한 무한 솔레노이드 2개가  다음과 같이 겹쳐져 있다고 하자.

큰 솔레노이드 안에 작은 솔레노이드를 쏙 집어넣은 꼴이다. (각 솔레노이드는 철심에 감겨있지 않고 공기로 차있다.)

 

안쪽에 있는 작은 솔레노이드 코일을 코일1 이라 하고 

바깥쪽에 둘러싼 큰 솔레노이드 코일을 코일2 라 하자.

그러면 각 코일이 만든 자계는 다음과 같이 계산 가능하다.

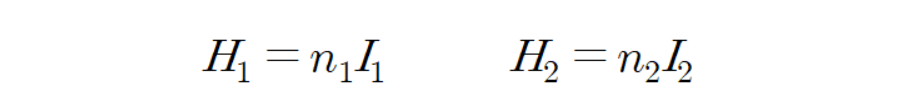
그리고 각 코일이 만든 자속밀도는 다음과 같이 계산 가능하다.

코일1솔레노이드와 코일2솔레노이드를 수직으로 자른 단면적이 있을 것이다.

(계산 실수 아닙니다. 이해가 잘 되지 않는다면, 위에서 소개한 "백터 면적분"을 참고해 주세요.)

이제 상호 인덕턴스를 정의를 보자.

상호 인덕턴스의 정의는 다음과 같다.

하지만 우리는 길이가 무한인 솔레노이드를 해석하고 있다.

그러므로 다음과 같이 단위 길이당 상호 인덕턴스를 유도해야 한다.

따라서 무한 솔레노이드의 상호인덕턴스는 다음과 같이 계산된다.