벡터의 외적

 

 

이번 편은 벡터의 외적에 대한 공식을 증명할 겁니다.

 

그 전에 벡터의 내적에 대한 증명이 궁금하신 분들께서는

https://pilgigo.tistory.com/entry/%EB%B2%A1%ED%84%B0%EC%9D%98-%EB%82%B4%EC%A0%81

벡터의 내적

여기를 참고해 주세요. (내적을 이용해서 외적을 증명할 겁니다.)

 

 

그럼 시작하겠습니다.

 

두 벡터의 외적은 다음과 같이 계산된다.

내적해서 0이 된다는 것은 수직관계임을 뜻한다. 왜냐면 내적의 의미가 나란한 성분의 곱을 뜻하는데, 결과값이 0 이므로 나란한 성분이 없음을 알 수 있다. 따라서 수직임을 의미한다.

방향을 쉽게 아는 방법은 오른손을 이용하는 방법이다. (이에 대한 설명은 생략하겠습니다.)

이렇게 외적은 X 로  표기한다. 

 

두 벡터가 3차원 공간인 직각좌표계에 있다면 다음과 같이 표시할 수 있다.

그리고 내적을 이용하여 다음과 같은 식을 유도할 수 있다.

여기서 잠깐 !

계속해서

이렇게 된다.  

즉. 외적의 크기는

이렇게 계산된다는 것을 알았다.

 

이제 방향에 대해 알아보자.

 

다음 두 벡터가 있다고 하자.

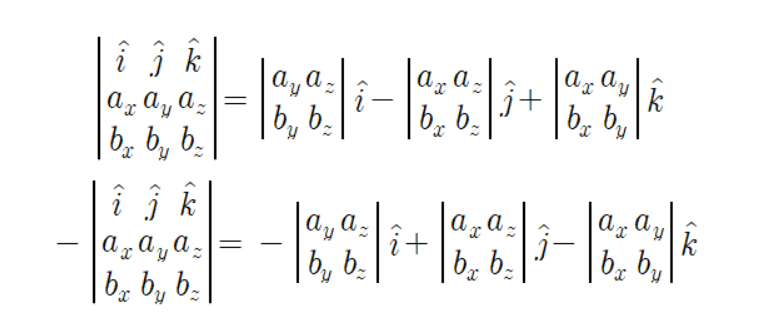
그리고 두 벡터는 다음과 같이 계산된다.

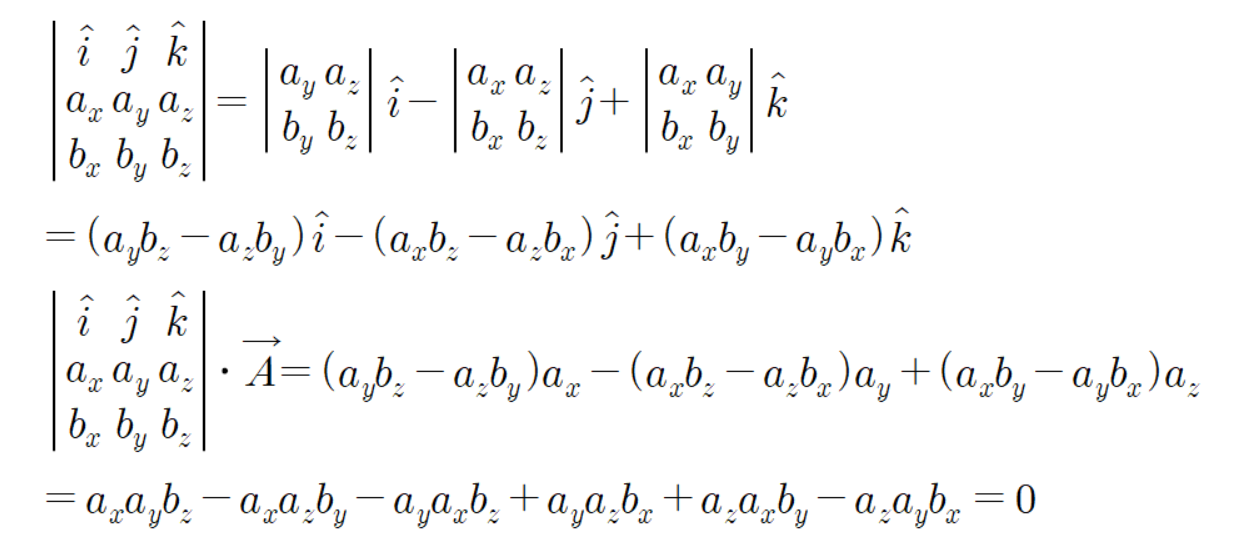
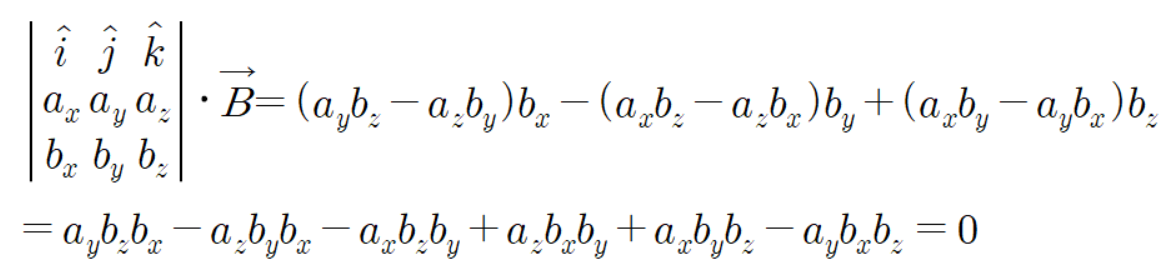
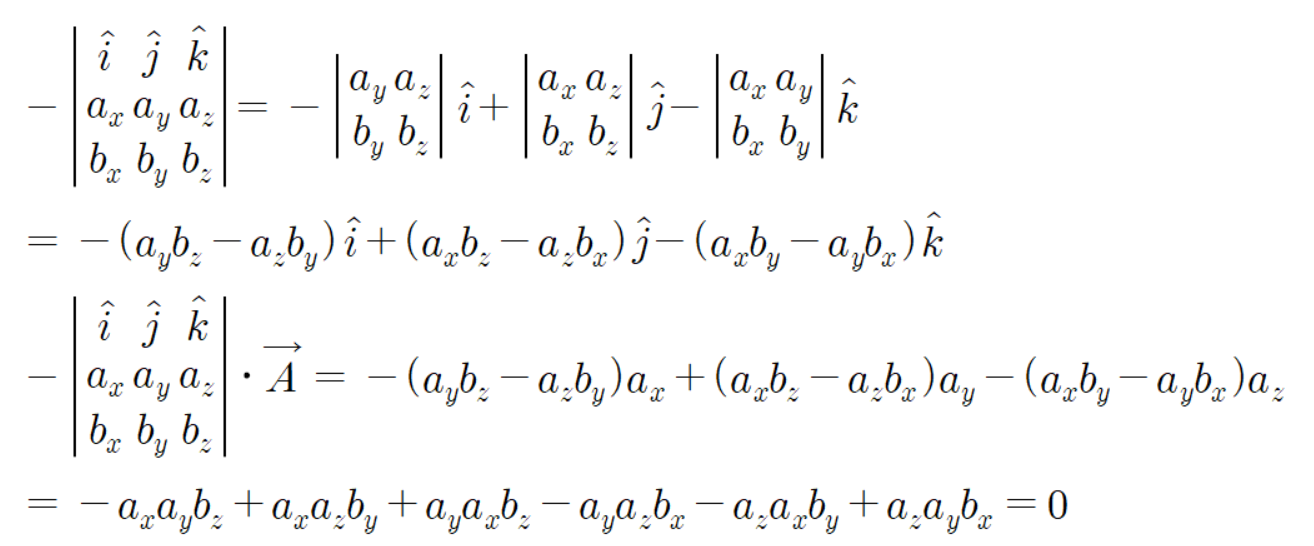
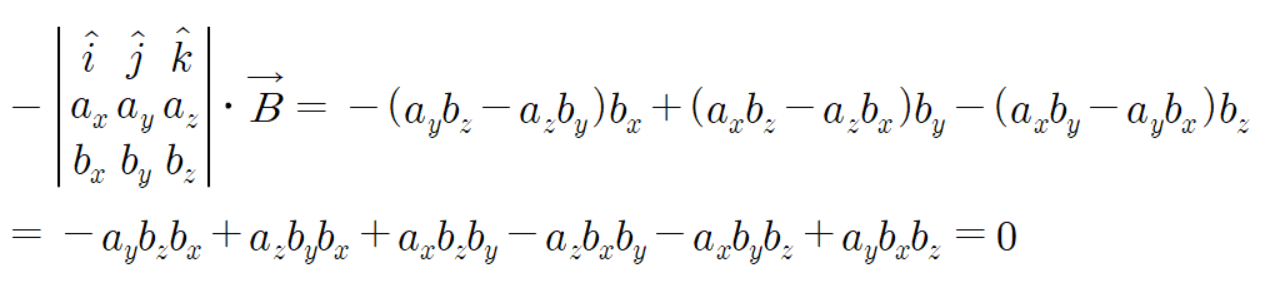
따라서

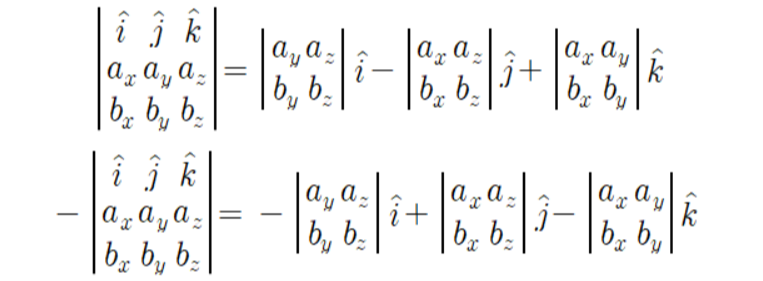
이 두 벡터들은

따라서

 

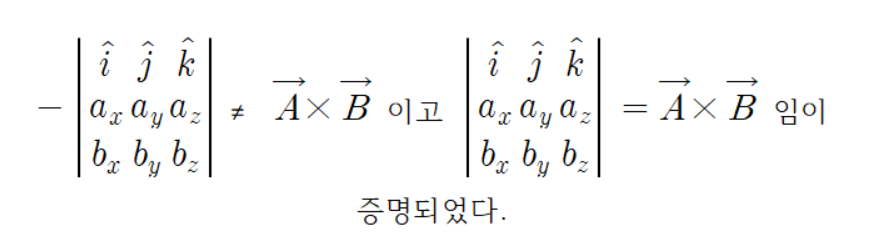
외적은 공간상에 있는 삼각형의 넓이를 구하는데 활용됨니다.

https://pilgigo.tistory.com/entry/%EA%B3%B5%EA%B0%84%EC%83%81%EC%97%90-%EC%9E%88%EB%8A%94-%EC%82%BC%EA%B0%81%ED%98%95-%EB%84%93%EC%9D%B4

공간상에 있는 삼각형 넓이

여기를 참고해 주세요.^^