2022. 8. 6. 20:50ㆍ수학
이번 편은 점근선에 대해 이야기할 겁니다.
시작하기 전 고등학교 내용을 잠깐 복습하겠습니다.
어떤 연속 함수가 있다고 하자.
그 함수의 식은 알지만 그래프 그림은 모르고 있는 상태라 가정하자.
그 식을 통하여 그래프를 그리는 것을 해보자.
그래프를 그리기 위하여
그 그래프의 극댓값과 극솟값의 좌표를 구하는 것과
변곡점의 좌표를 구해야 하고
각 구간마다 그려지는 그래프의 증가와 감소를 판정해야 하며
각 구간마다 그려지는 그래프의 오목과 볼록을 판정해야 한다.
이들은 미분을 통한 계산으로 구할 수 있다.
그리고 마지막으로
극한을 이용하여 점근선의 방정식을 알아본다.
점근선은 기본적으로 직선이다.
그러니 점근선은 직선의 방정식으로 표현 가능하다.
점근선은 다음과 같은 방법으로 구할 수 있다.

여기까지는 여러분들께서 고등학생 때 공부하셨으므로 잘 알고 계실 겁니다.
(그러니 위 내용에 자세한 증명은 생략하겠습니다.)
이번 편에서 저와 함께 알아볼 내용은, 위 내용보다 심화된 이야기입니다.
그럼 시작하겠습니다.
첫 번째로 알아볼 상황은
다음과 같은 함수의 점근선이 수평으로 있다고 하자.

이때 도함수의 극한은 얼마일까?

우리는 이를 알아내기 위해 로피탈의 정리를 사용해 보자.
우선

두 번째로 알아볼 상황은
다음과 같이 점근선이 대각선일 때 이다.

이때 도함수의 극한은 얼마일까?
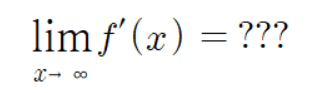
우리는 이를 알아내기 위해 위에서 정리한 내용을 이용해 보자.
우선
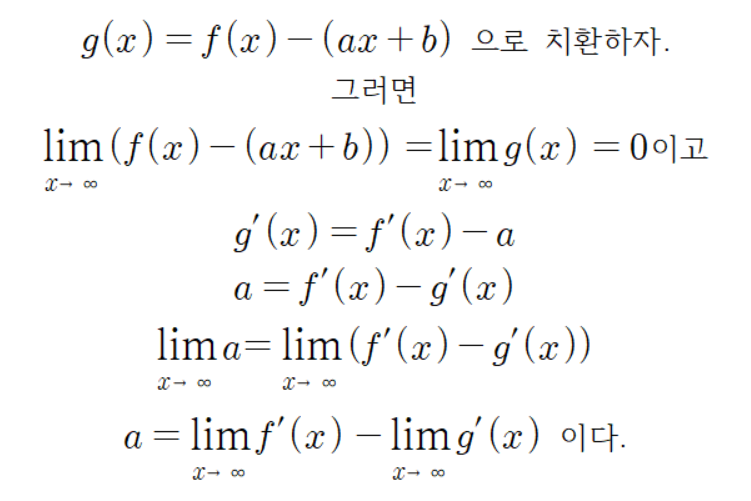
우리는 위에서
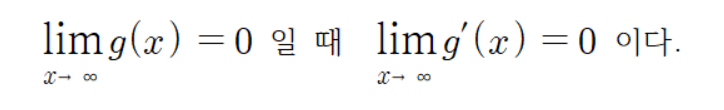
라는 사실을 로피탈 정리로 증명했다.
따라서
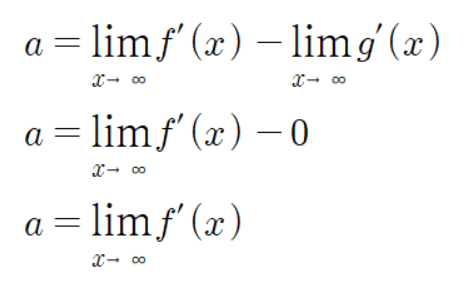
이다.
이로써 우리는,
점근선이 있는 함수의 도함수를
무한대로 극한을 보낼 때
무조건 수렴한다는 사실을 알아냈다.
그리고 그 수렴값이
점근선의 기울기 값과
같다는 것도 알았다.
그렇다면 반대로
도함수가 무한대로 갈때 수렴하면
원래 함수는 무조건 점근선이 존재할까?
그렇지 않다.
그에 대한 대표적인 예시로
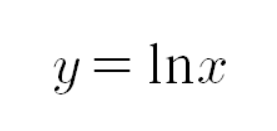
이 함수가 있다.
자연로그 함수는 점근선이 x=0말곤 존재하지 않는다.
위 함수를 미분하면
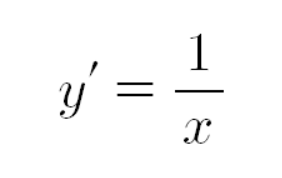
인데, 이 함수를 다음과 같이 극한을 보내면
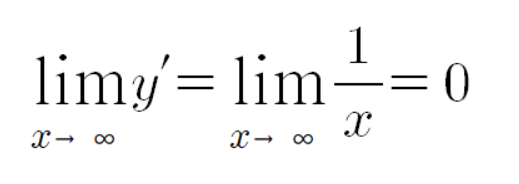
이므로 기울기가 0인 수평 점근선이 있을것 같지만,
그딴건 존재하지 않는다는 것을 우리는 알고 있다.
'수학' 카테고리의 다른 글
| 선형대수학 시리즈 1편(소거법칙) (0) | 2024.04.17 |
|---|---|
| 공간상에 있는 삼각형 넓이 (0) | 2022.09.10 |
| 벡터의 외적 (0) | 2022.05.29 |
| 벡터의 내적 (0) | 2022.05.15 |
| 클레로의 정리 (0) | 2022.05.09 |