2024. 5. 9. 16:55ㆍ수학
이번 편은 기저에 대한 필요충분조건 정리를 알아보겠습니다.
선형대수학 시리즈 7편은
선형대수학 시리즈 7편(선형종속)
이번 편은 선형종속이 되는 필요충분조건에 관한 정리를 소개하겠습니다. 선형대수학 시리즈 6편은 https://pilgigo.tistory.com/entry/%EC%84%A0%ED%98%95%EB%8C%80%EC%88%98%ED%95%99-%EC%8B%9C%EB%A6%AC%EC%A6%88-6%ED%8E%B8
pilgigo.tistory.com
여기를 참고해 주세요.
그럼 시작하겠습니다.
이번에 알아볼 정리는 다음과 같다.

이제 증명해 보자.
필요충분조건을 증명하는 것이므로 '필요한 조건' 임을 증명해야 하고 '충분한 조건' 임을 증명해야 한다.
그러므로

다음 두 가지 명제를 증명해 보자.
첫 번째 명제는 다음과 같다.

두 번째 명제는 다음과 같다.

먼저
첫 번째 명제 부터 증명해 보자.


고로 귀류법에 의해

그리고

여러해라는 조건에서 G이(가) 선형종속 이라는 증명은 다음과 같다.

그러면 다음과 같이 계산할 수 있다.

이 식에 대하여

이다.
다시말해

참고로 자명해란 모든 스칼라가 0인 해를 말하고
비자명해란 자명해가 아닌 해를 말한다.
따라서

정리하여

고로 귀류법에 의해

우리는 조금 전에

고로

첫 번째 명제 증명이 끝났다.
이제 두 번째 명제를 증명해 보자.
두 번째 명제를 다시 한번 보자.

이를 증명해 보자.

다시말해

즉, G은(는) V을(를) 생성한다.
그리고

다시말해
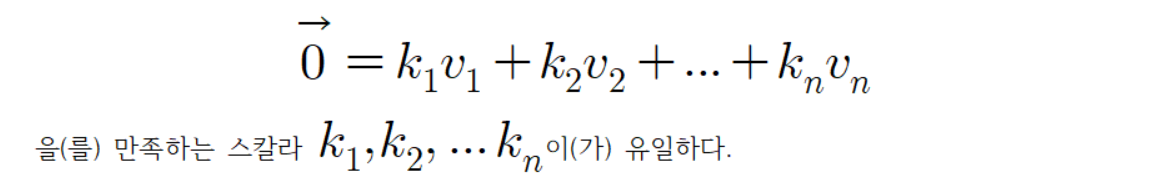
즉, G은(는) 선형독립이다.
정리하여

생성과 선형독립을 동시에 만족하는 것은 기저를 의미한다.
두 번째 명제도 증명 되었다.
첫 번째 명제도 참 이고 두 번째 명제도 참 이므로

그러므로 기저의 필요충분조건이 될 수 있다.
선형대수학 시리즈 9편은
선형대수학 시리즈 9편 (생성집합속 기저존재)
이번 편은 벡터공간을 생성하는 집합속에 기저를 포함함을 증명해 보겠습니다. 그럼 시작하겠습니다. 이번 편에 소개할 첫 번째 정리는 다음과 같다.(단, G는 유한집합이다.) 이제 증
pilgigo.tistory.com
여기를 참고해 주세요.
'수학' 카테고리의 다른 글
| 선형대수학 시리즈 9편(생성집합속 기저존재) (0) | 2024.05.12 |
|---|---|
| 선형대수학 시리즈 7편(선형종속이 되기 위한 필요충분조건) (0) | 2024.05.09 |
| 선형대수학 시리즈 6편 (0) | 2024.05.08 |
| 선형대수학 시리즈 4편(부분공간 교집합) (0) | 2024.05.02 |
| 선형대수학 시리즈 3편 (부분공간) (0) | 2024.05.01 |