2021. 10. 22. 20:14ㆍ물리
이번 편은 용수철 운동이 정말 삼각함수인지에 대해 증명해 볼 겁니다.
그럼 시작하겠습니다.
다음과 같이 천장에 물체가 용수철로 매달려 있다 하자.

이 용수철에 매단 물체는 다음과 같은 단진동 운동을 한다.
(벽은 고정되어 있고 중력이 없으며 공기의 저항과 마찰 또한 없는 상황에서 실험한 상황이다.)


그림에 나와있는 S와(과) t에 대한 그래프를 함수로

라고 하자.
f(t) 함수를 구하기 위해 필요한 3가지 식을 구해 보자.
우선

이 f(t) 함수 그래프의 일부분인 파란색 네모칸 안에 있는 그래프만 그대로 새로운 좌표계에 옮겨서
다음과 같이 새로운 함수 그래프를 정의하자.

이 그래프의 함수식은

이다.
이 함수식을 이용하여 필요한 3가지 식들 중에서 2가지를 구해 보자.
첫 번째로 구할 식은 다음과 같다.


두 번째로 구할 식은 다음과 같다.
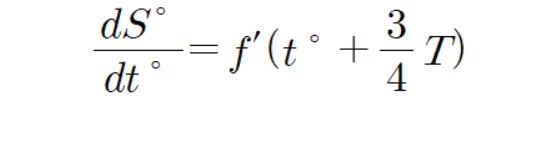
이렇게 필요한 식 첫 번째와 두 번째를 구했다.
이제 나머지 세 번째 식을 구해보자.
위치와 힘 벡터의 함수는 다음과 같다.
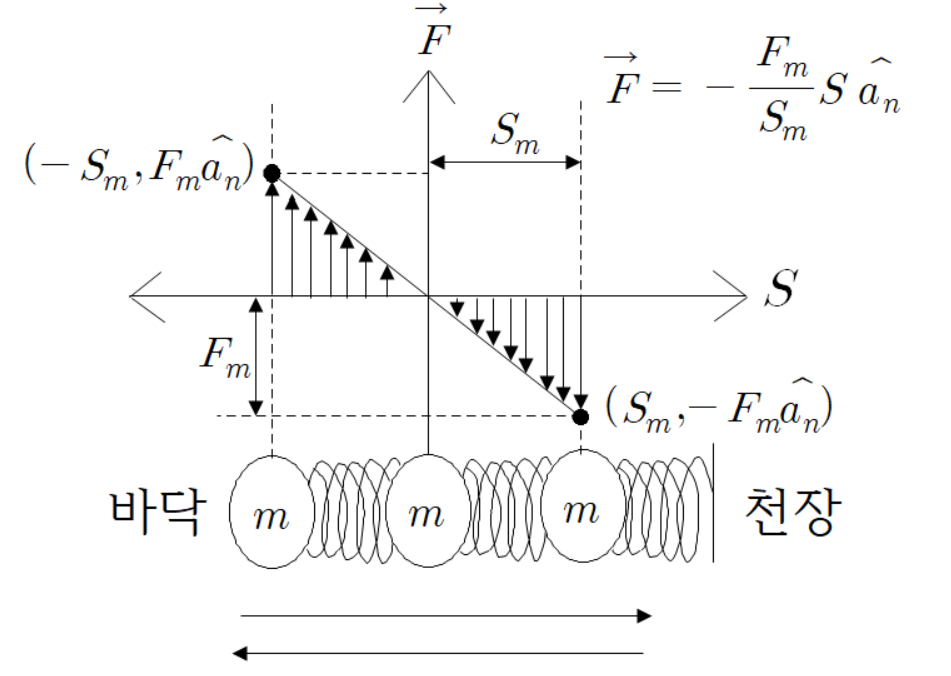

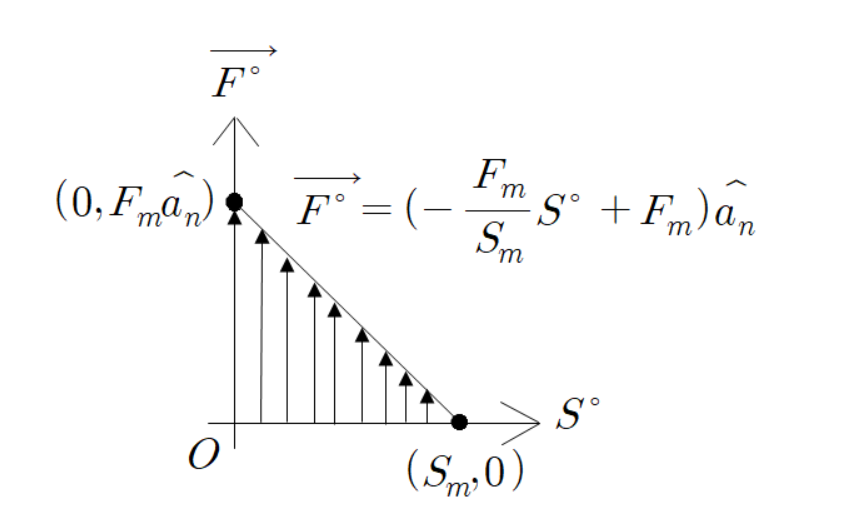
이 그래프의 기울기를 k 이라 하자.
k은(는) 기울기 이므로
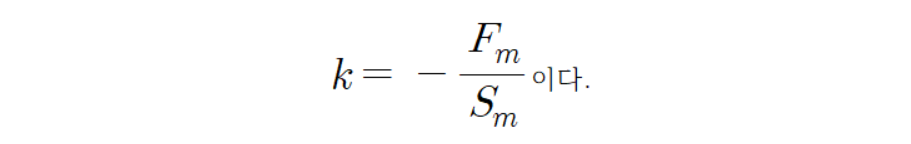
이를 이용하여 다음과 같이 계산할 수 있다.
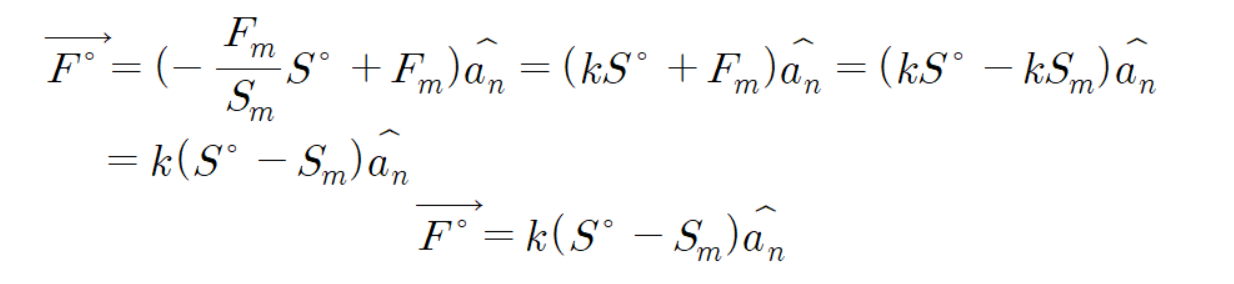
이 식을 통해 힘을 위치로 적분하여 용수철이 한 일을 구해 보자.

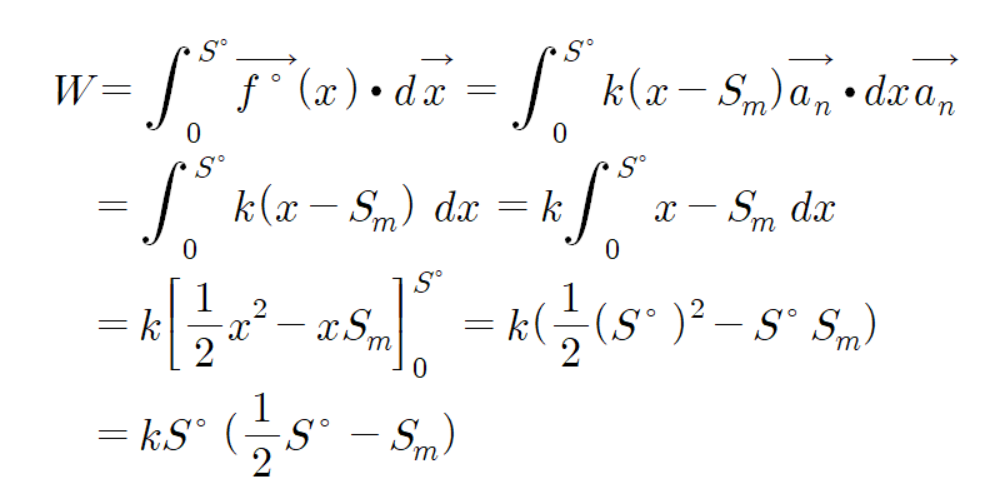
물체가 받은 일의양은 곧바로 운동에너지가 된다.
물체의 운동에너지를 E라 하자.
그러면 E=W 이다.
운동에너지는 다음과 같다.
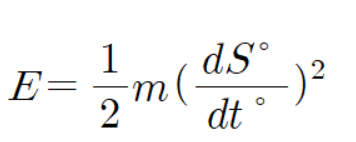
E=W 이므로
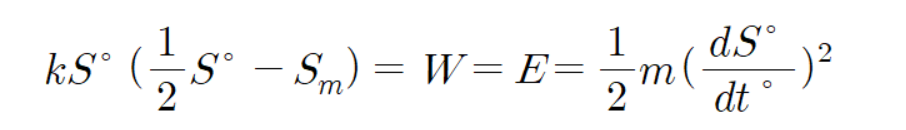
이다.
그러므로 다음과 같이 구할 수 있다.
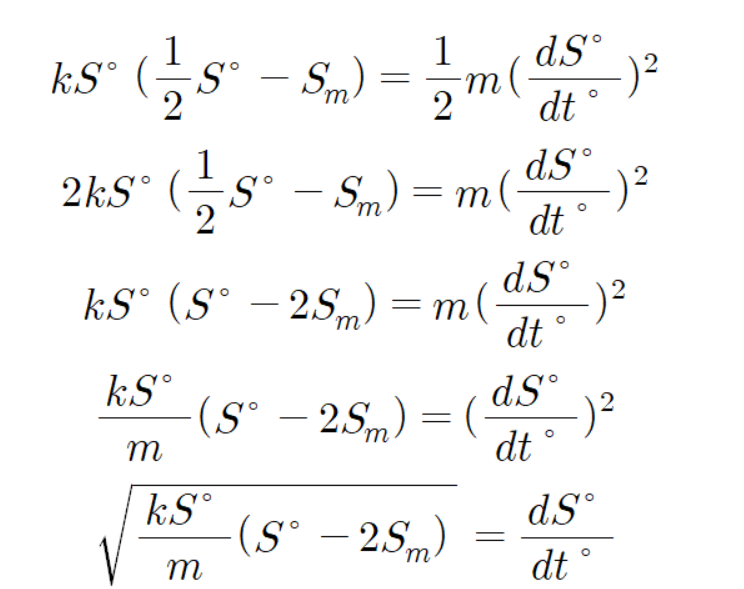
이것이 우리가 찾고자 했던 세 번째 식이다.
이렇게 구한 다음 세가지 식을 모아보면 다음과 같다.
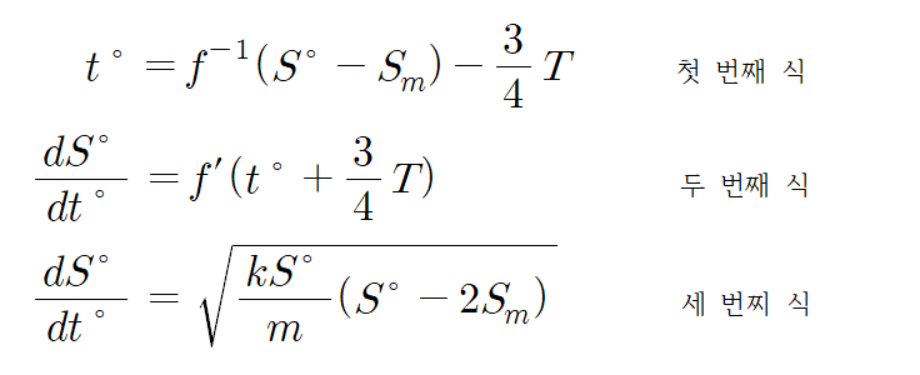
이제 수학만 남았다.
먼저 두 번째 식에다 첫 번째 식을 대입하여 계산해 나간다.


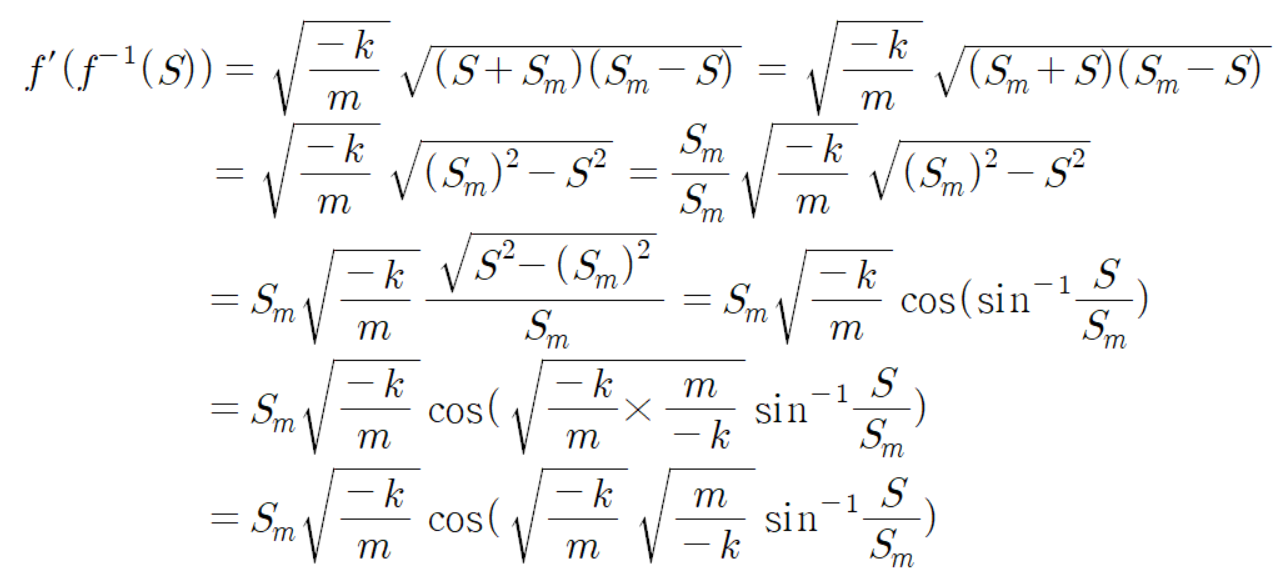
따라서 다음과 같은 결론을 낼 수 있다.
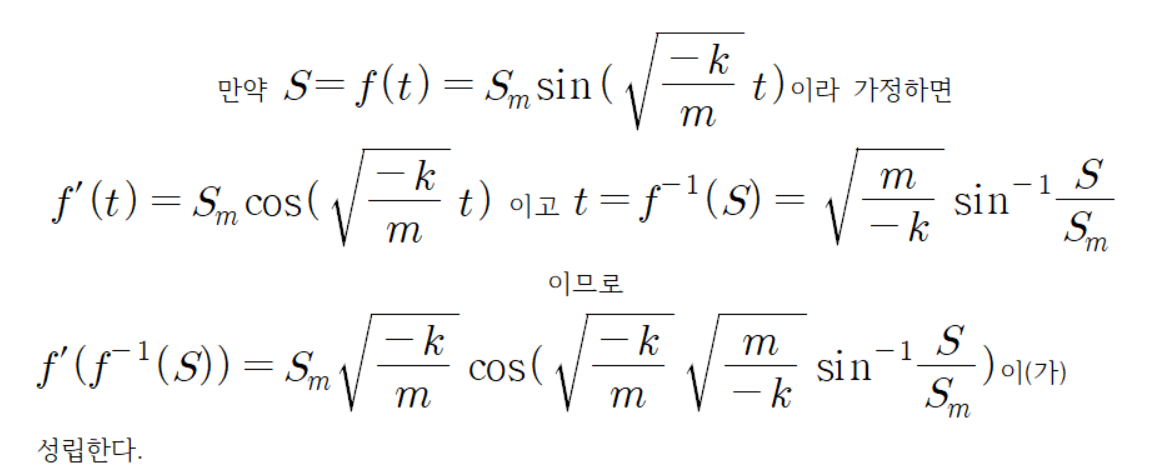
하지만
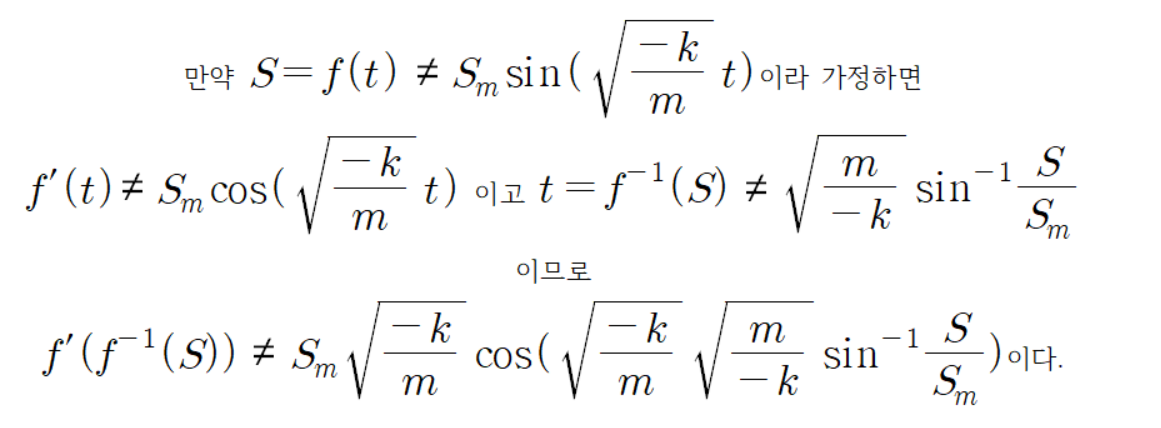
이는 모순 이므로 귀류법에 의해
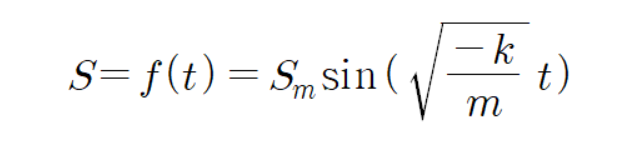
임을 알 수 있다.
증명끝.
'물리' 카테고리의 다른 글
| 인덕터에 저장된 에너지 (R-L직렬 직류 회로 3편) (0) | 2021.10.30 |
|---|---|
| R-L직렬 직류 회로 2편 (0) | 2021.10.30 |
| R-L직렬 직류 회로 (0) | 2021.10.28 |
| 두 기둥에 힘의 비율 (0) | 2021.10.26 |
| 탈출 속도 (2) | 2021.10.25 |