2021. 11. 18. 00:32ㆍ수학
이번 편은 고등학교 미적분2 교육과정에 배우는
삼각함수 합성공식을 일반화 하여
더 어렵고 유용한 삼각함수 합성공식을 알아볼 겁니다.
그럼 시작하겠습니다.
고등학교에서 배우는 삼각함수 합성공식은 다음과 같다.
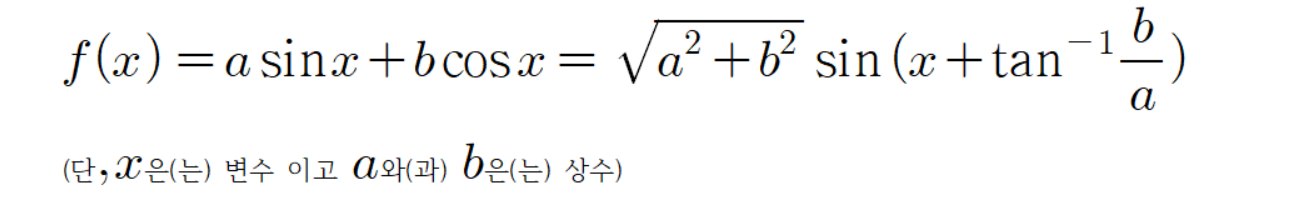
그리고 우리가 알아볼 공식은 다음과 같다.

이제 증명해 보자.
이를 증명하기 위해 다음과 같은 9가지 경우들을 모두 해석하고 증명해야 한다.

먼저

공식을 증명해 보자.
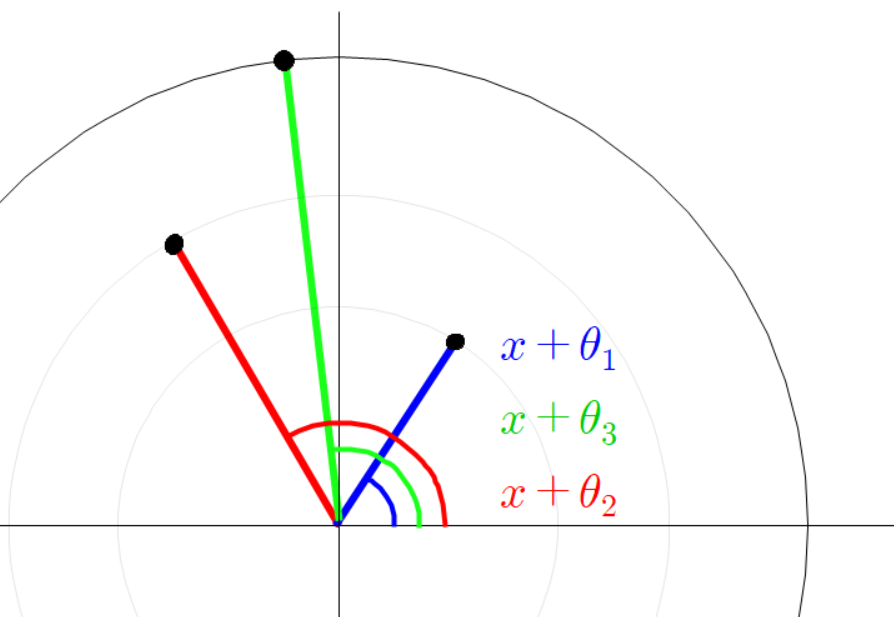
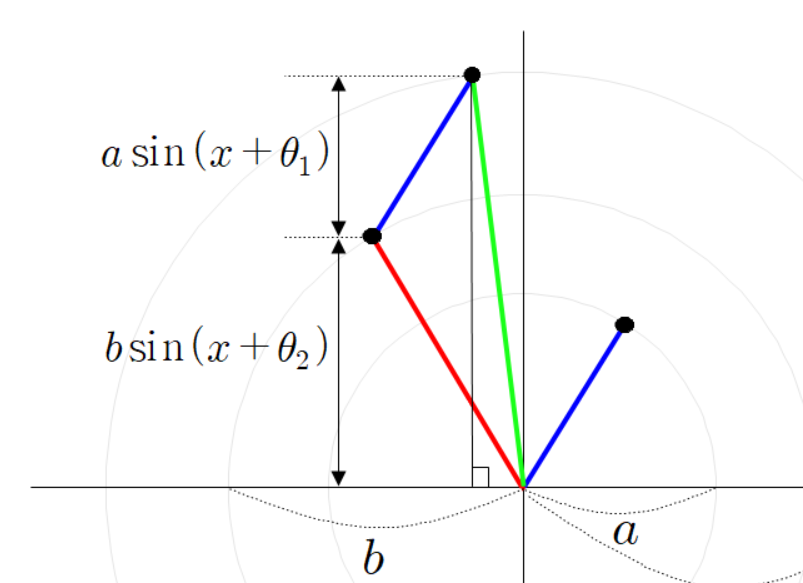
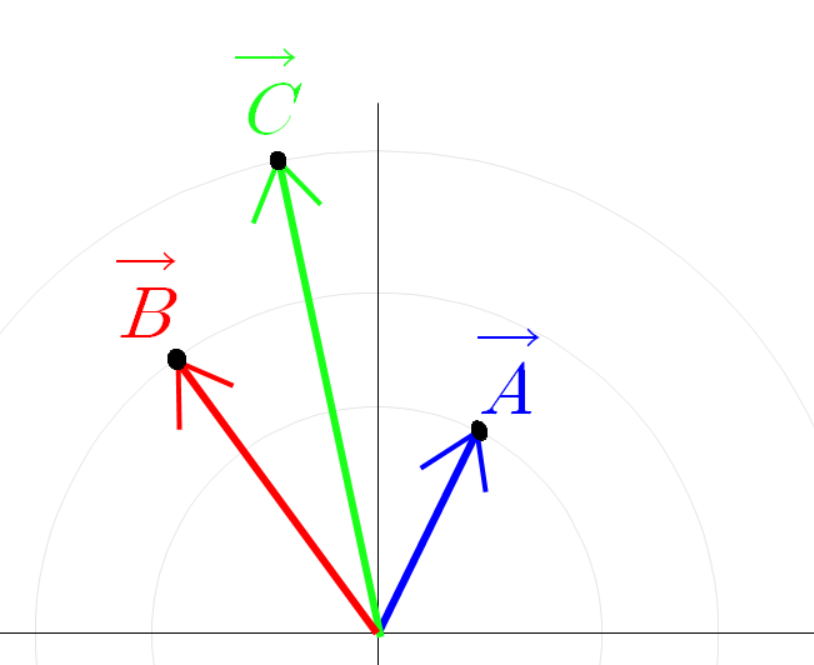
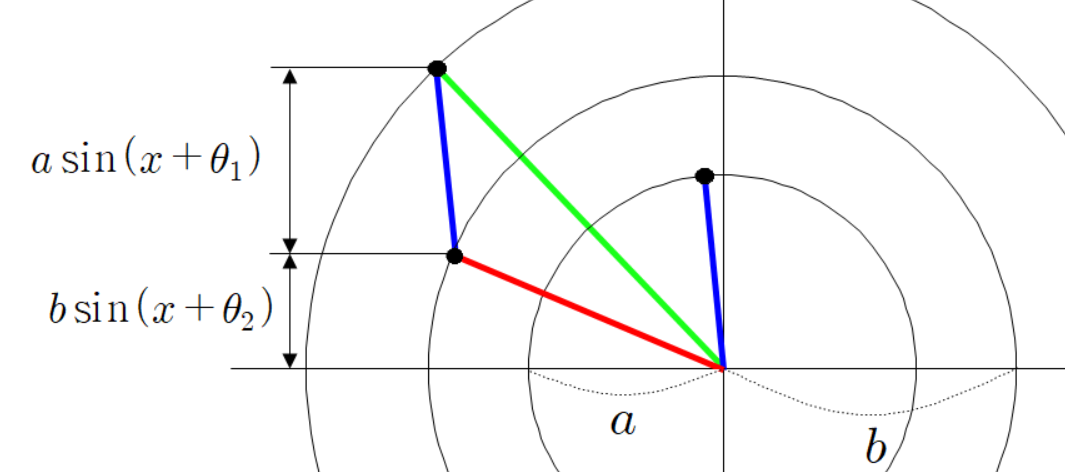
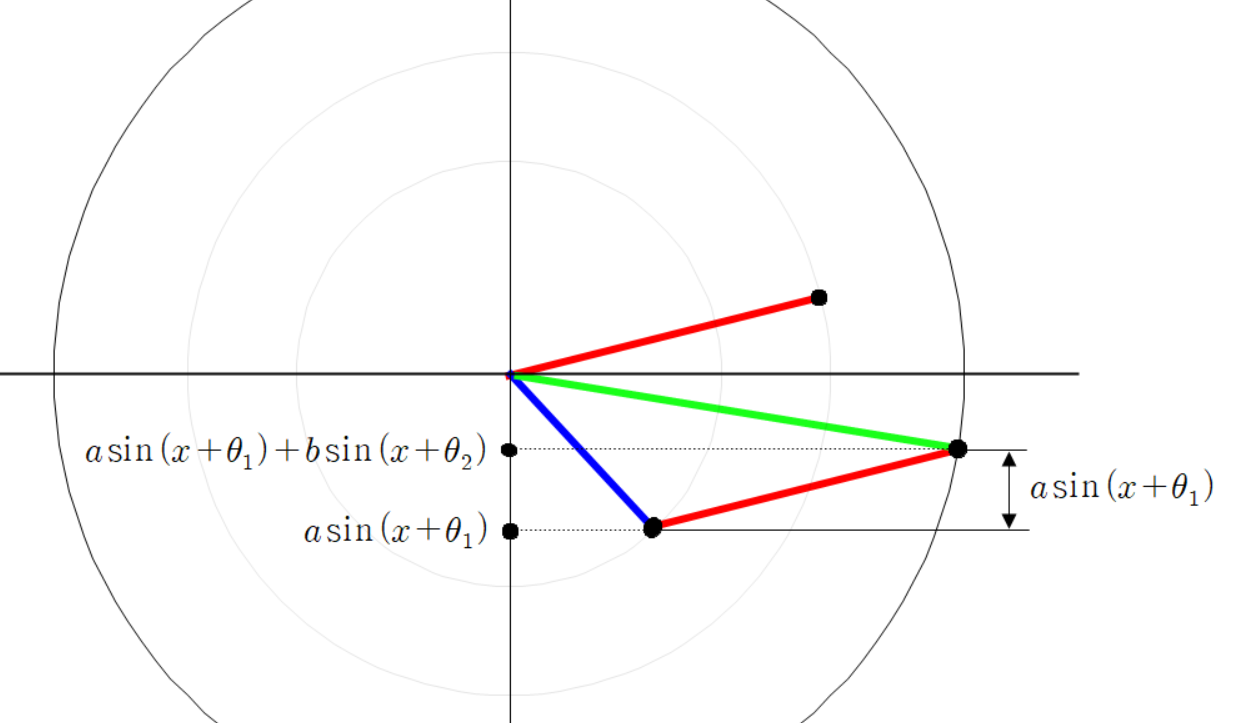
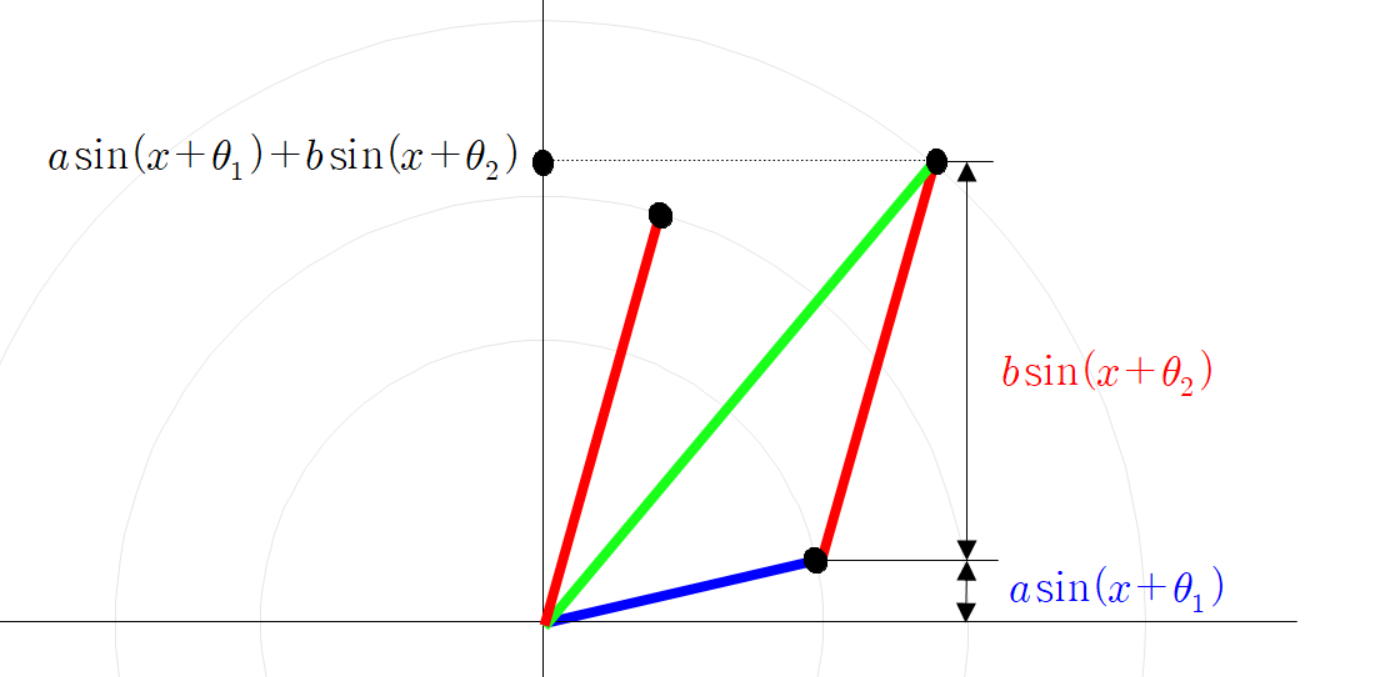
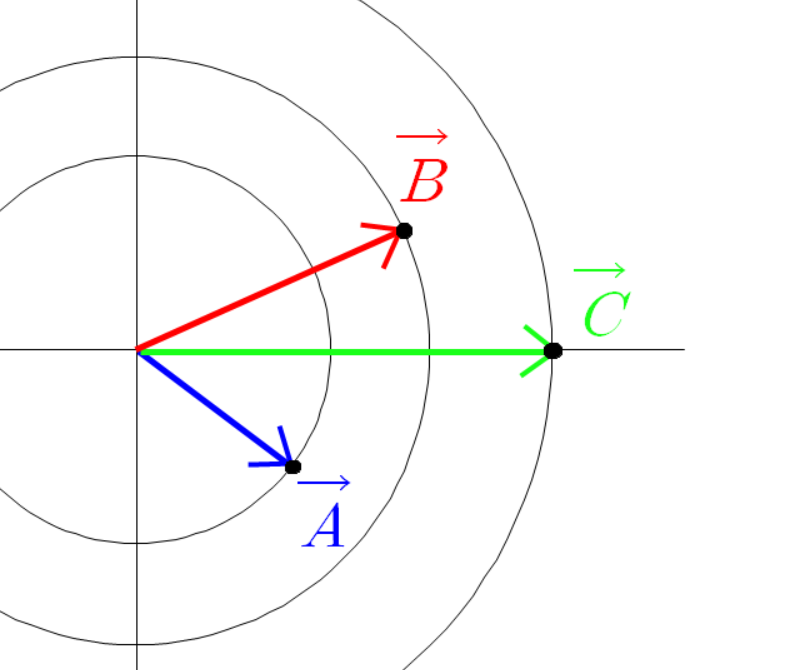
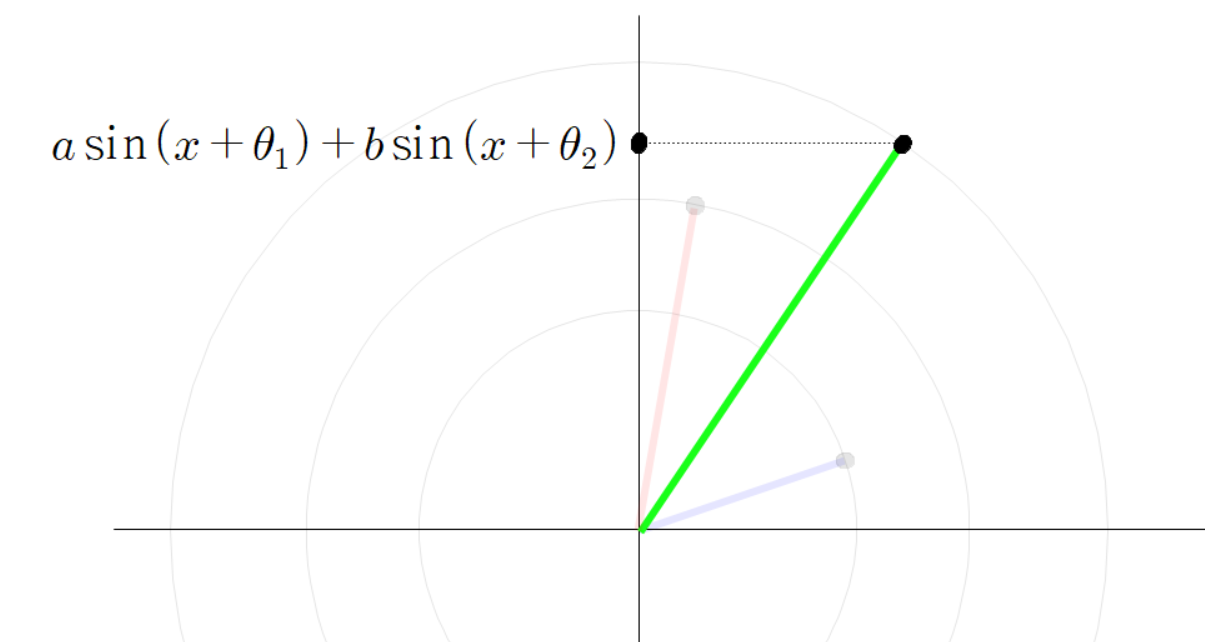
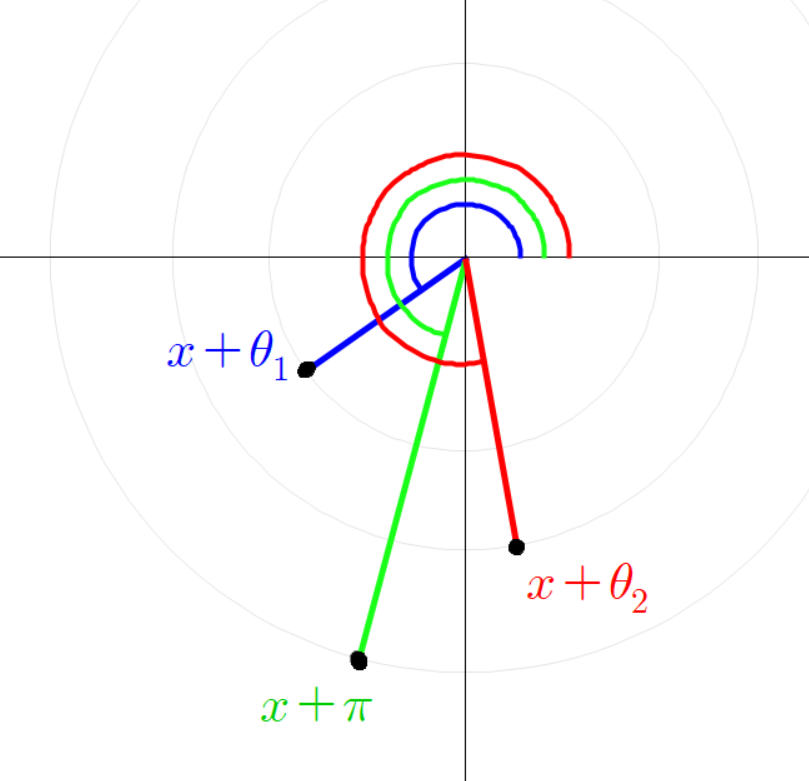
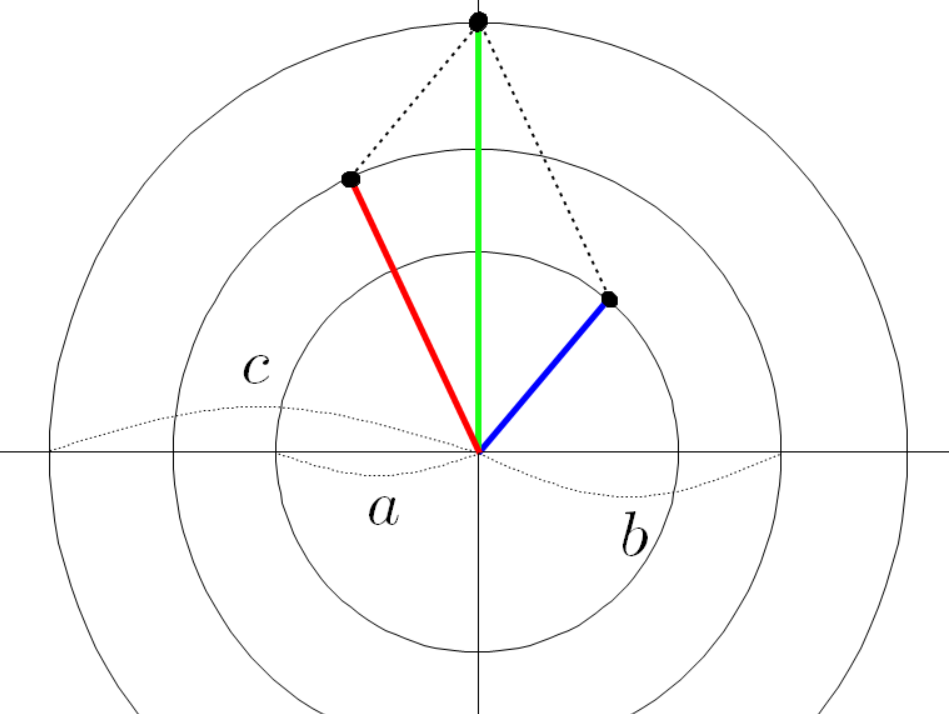
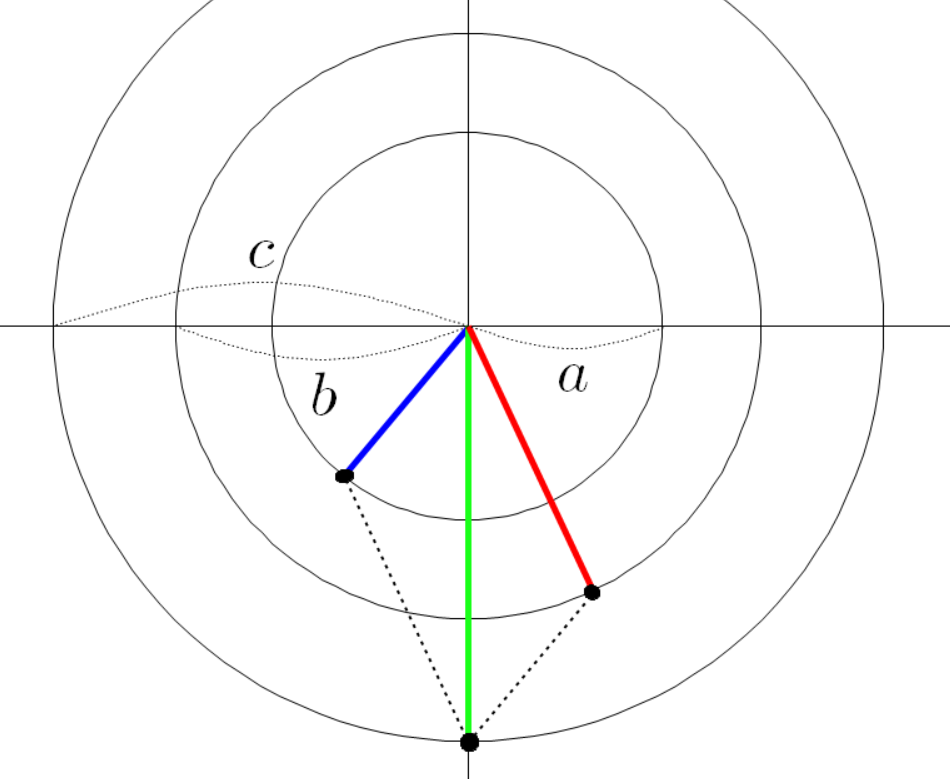
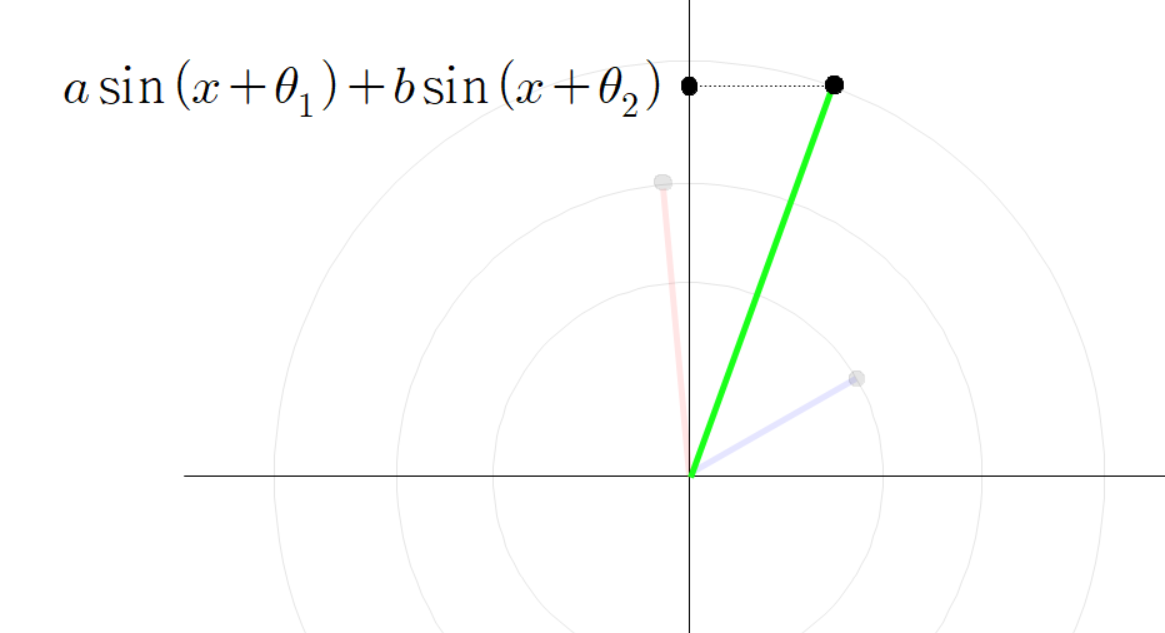
좌표 평면에 빨간 선분과 파란 선분이 원점에 붙어 있다고 하자.
그리고
빨간 선분과 파란 선분의 각도를 다음과 같이 정의 하자.

그리고 다음과 같이
빨간 선분과 평행하고 파란 선분과 평행한 두 점선을 그려 보자.
그리고
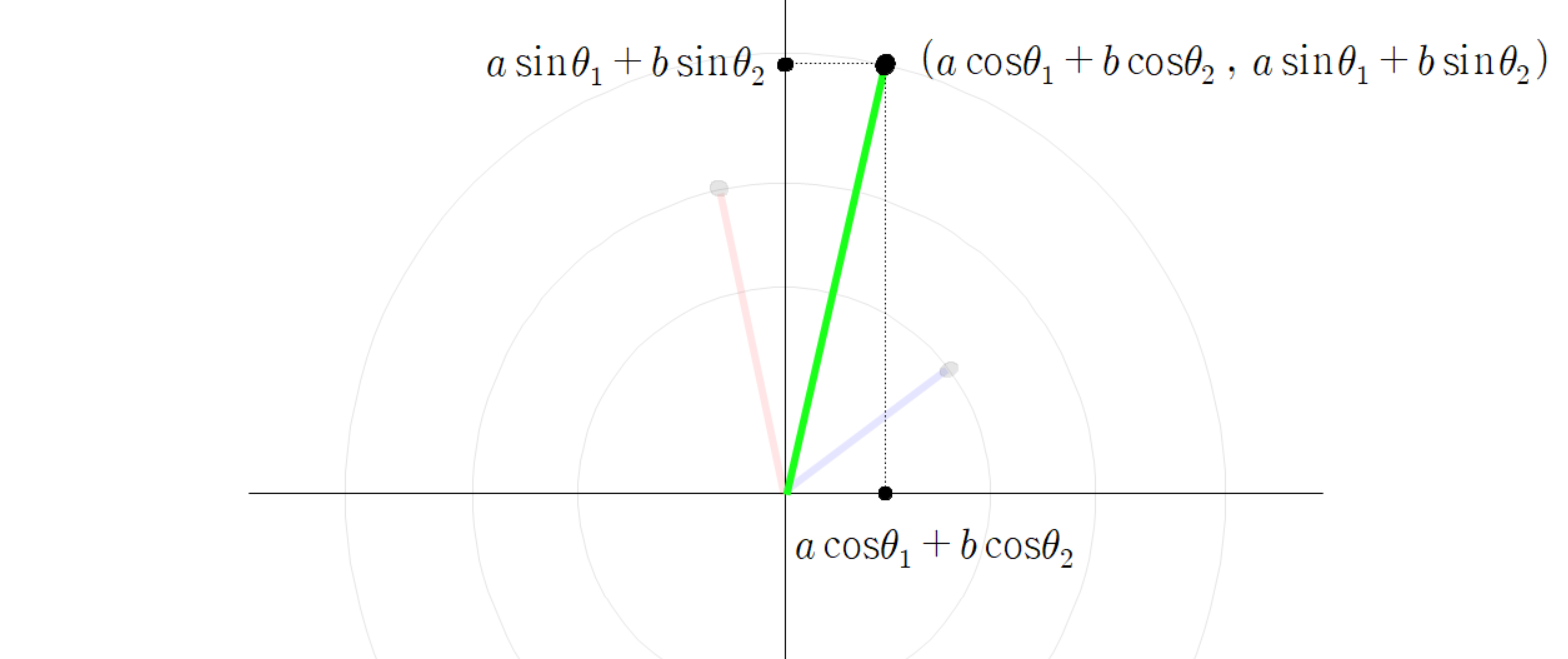
두 점선이 교차하는 곳에 교차점을 찍자.

두 점선이 만나는 교차점과 원점을 잇는 초록색 선분을 그리자.
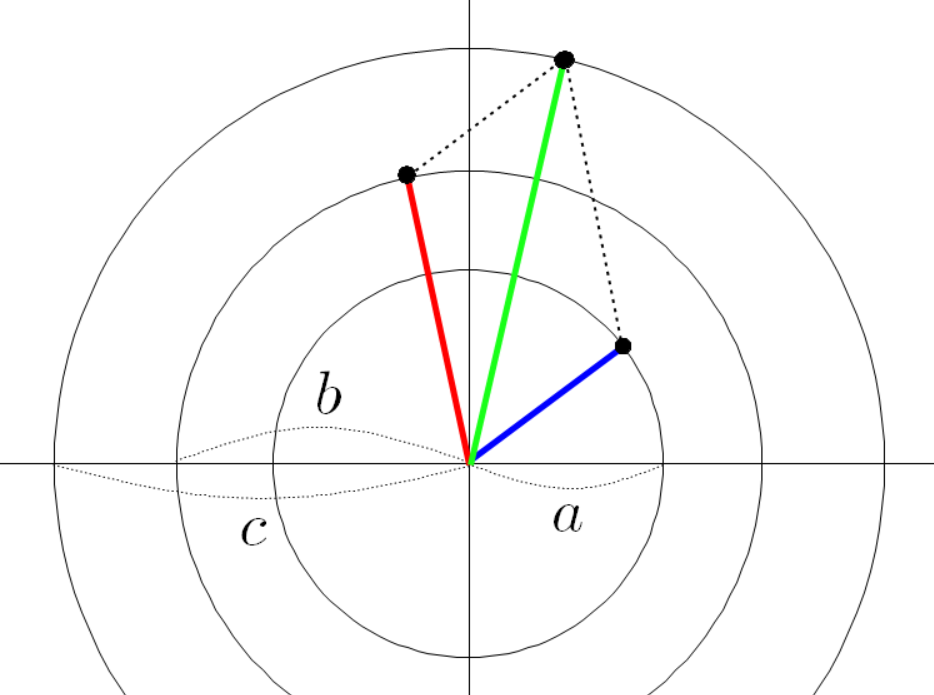

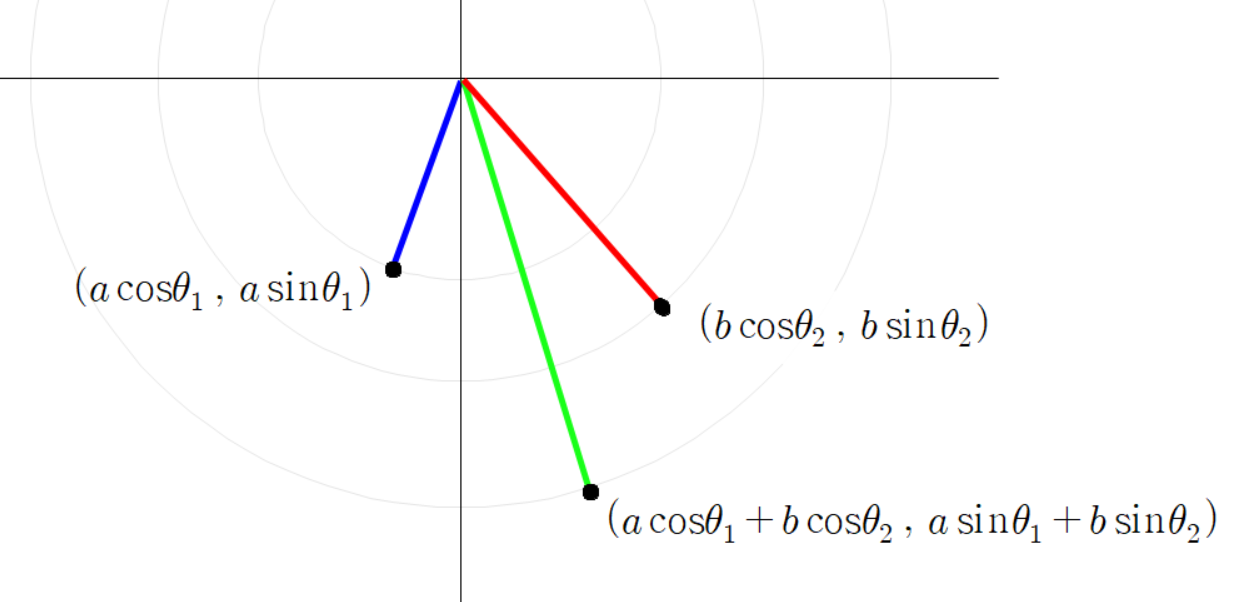
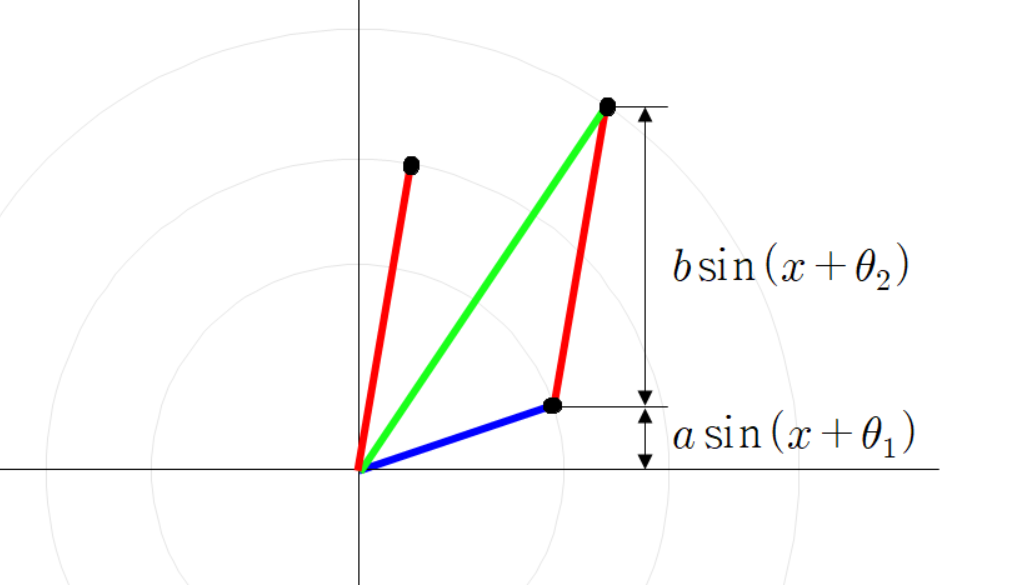
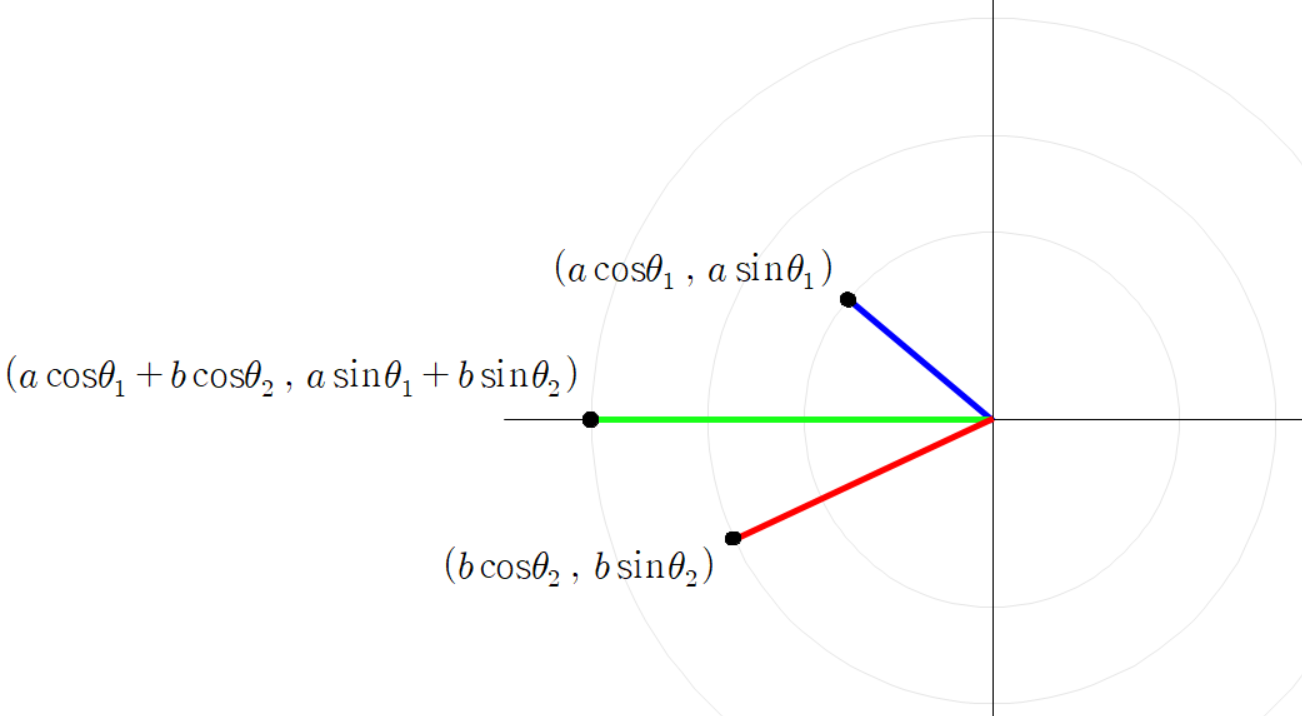
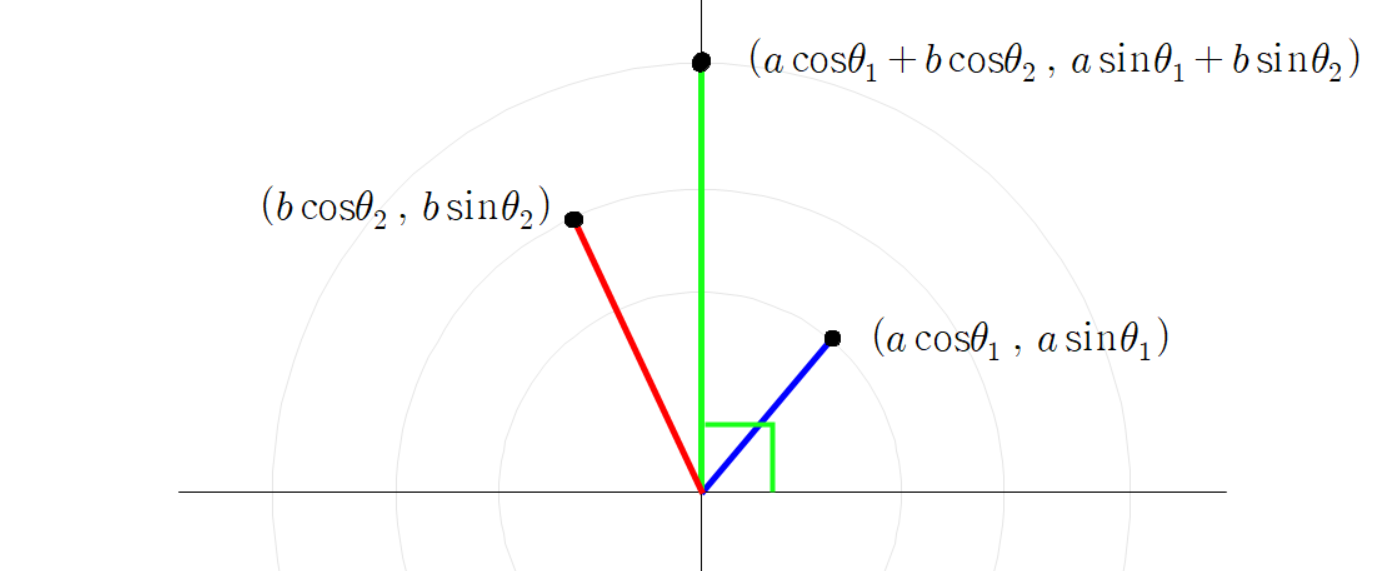
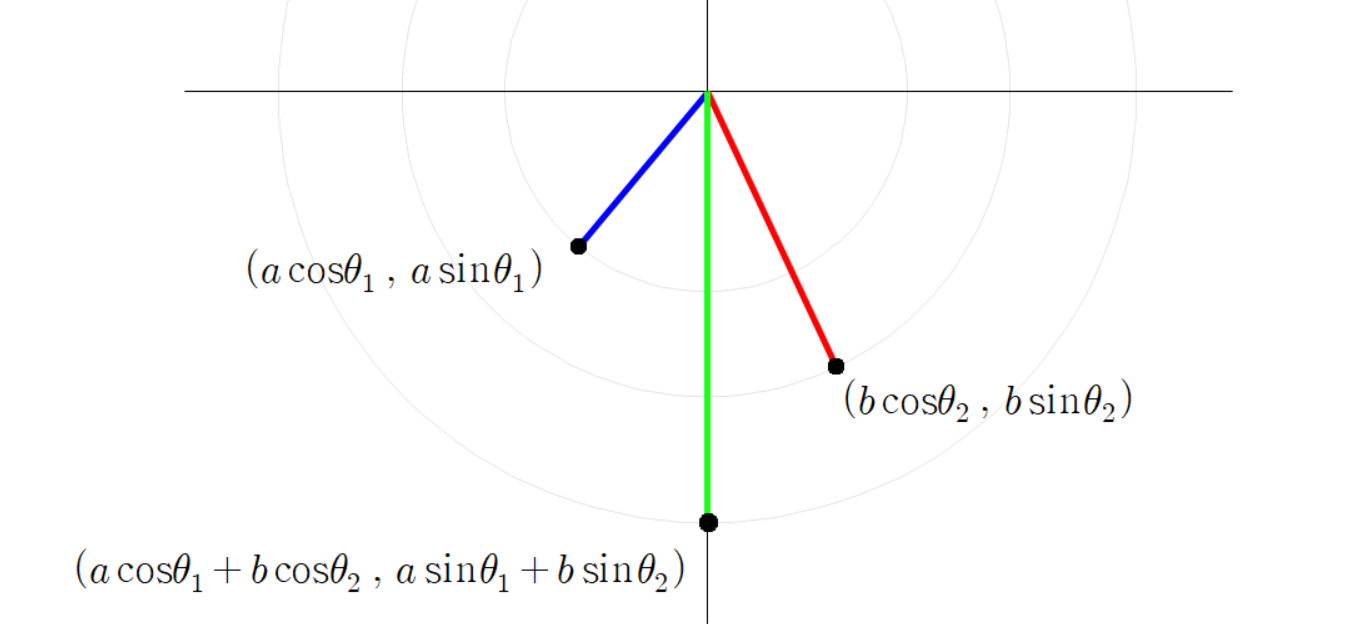
세 점들의 좌표는 다음과 같다.
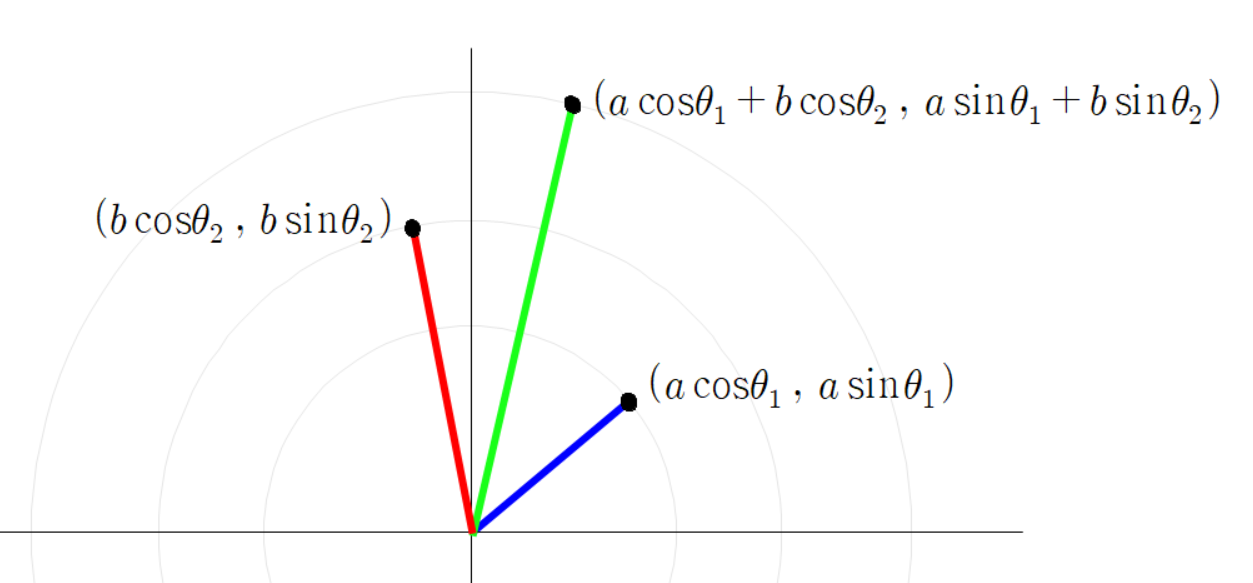
초록색 선분 끝 점의 좌표가 이렇게 계산되는 이유는
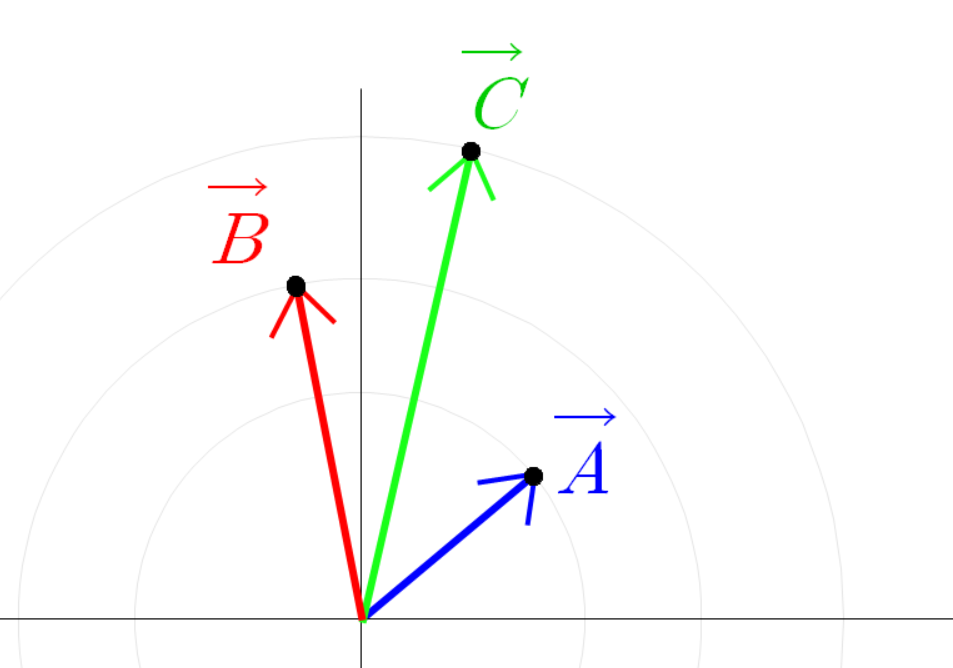
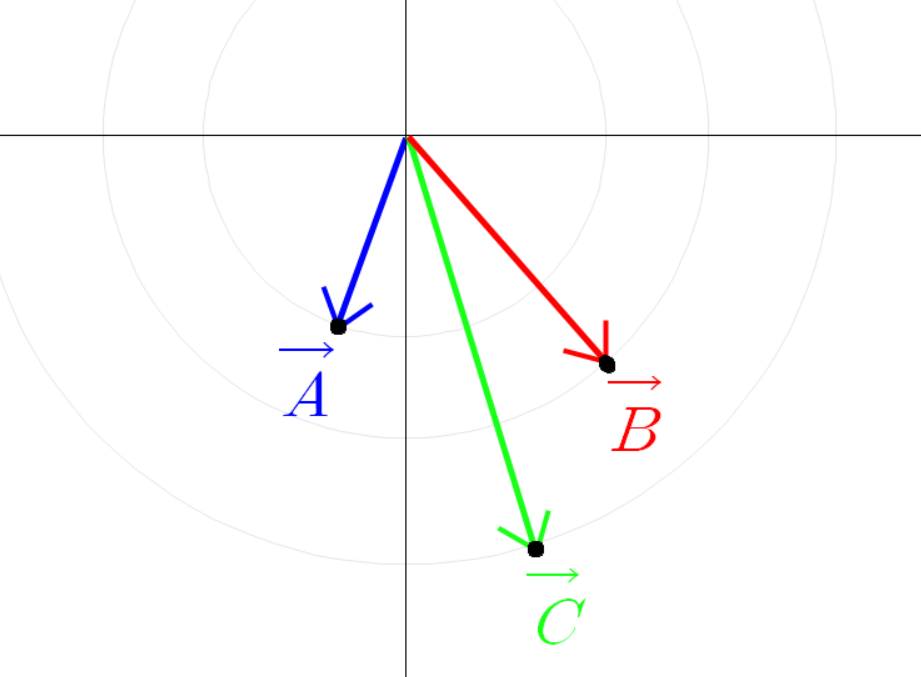
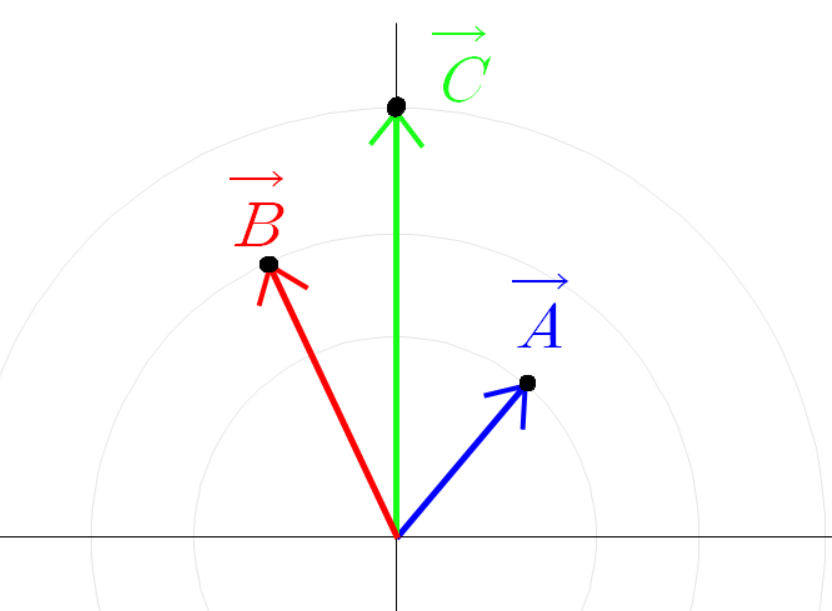
파란 선분 빨간 선분 초록 선분을 벡터로 본다면
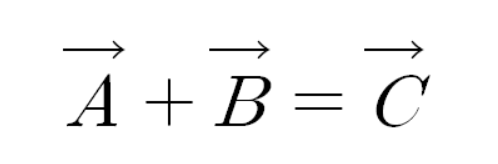
이(가) 성립하기 때문이다.
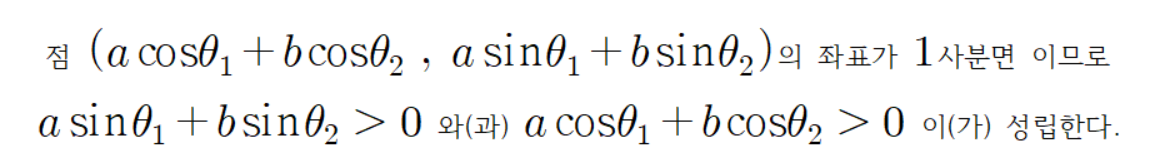
두 점 사이의 거리를 구하는 공식인 피타고라스 정리를 이용하여
초록색 선분의 길이는 다음과 같이 계산 할 수 있다.
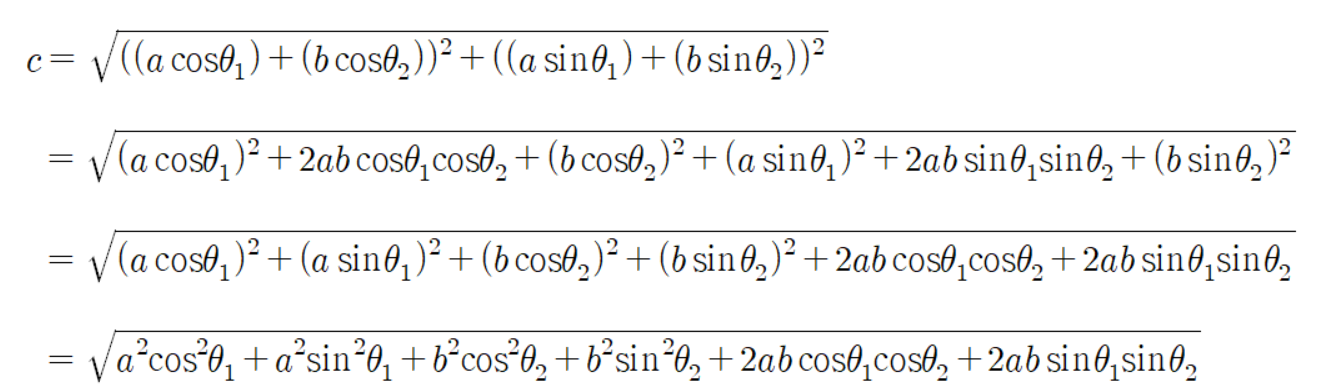
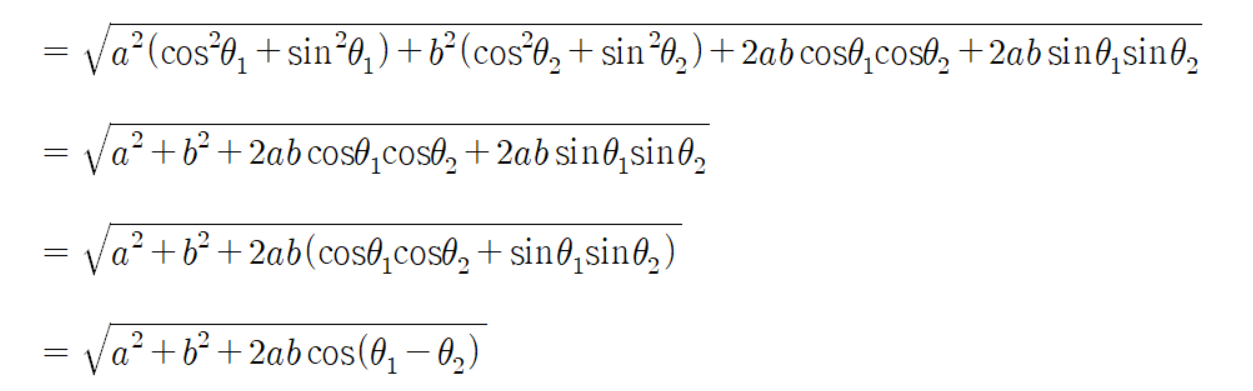
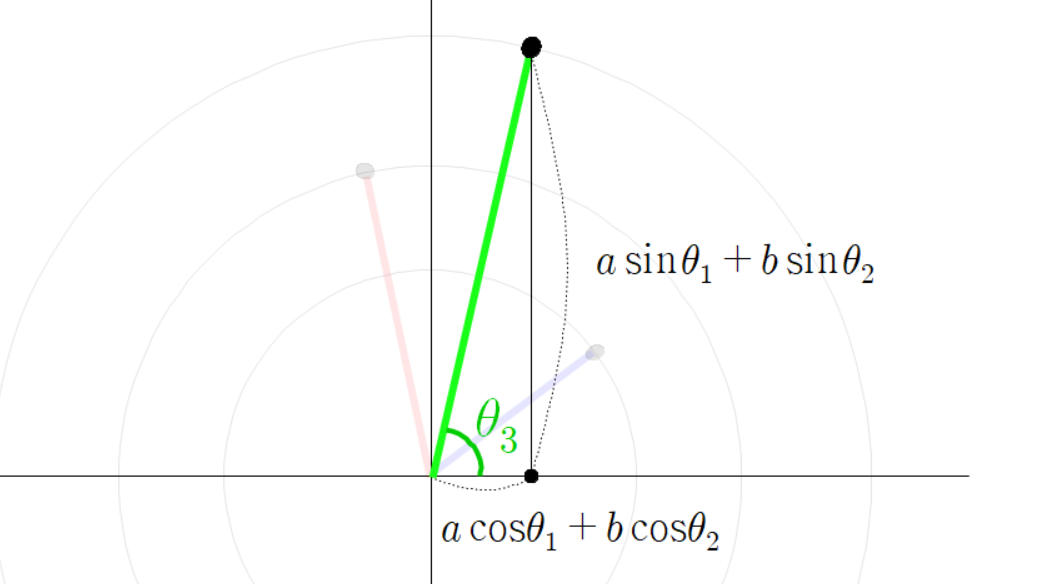
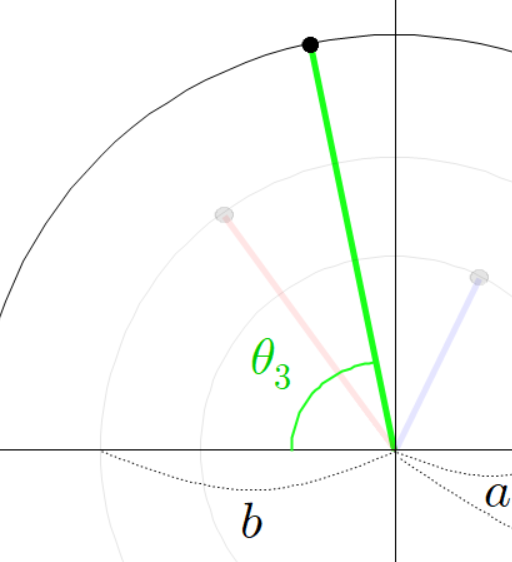
그리고 초록색 선분의 각도를 다음과 같이 정의하자.
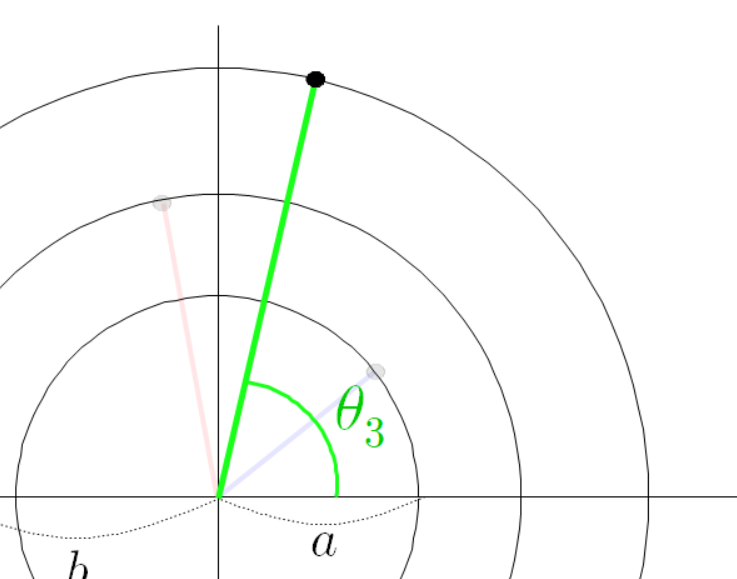
참고로

이 각도는 다음과 같이 계산 할 수 있다.
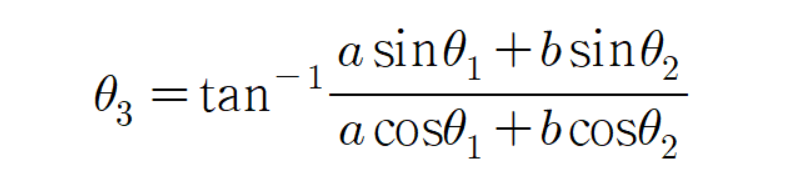
이유는 다음과 같다.
조금 전에 알아낸 초록색 선분 끝점의 좌표는
이러하기 때문에
이다.
그러므로
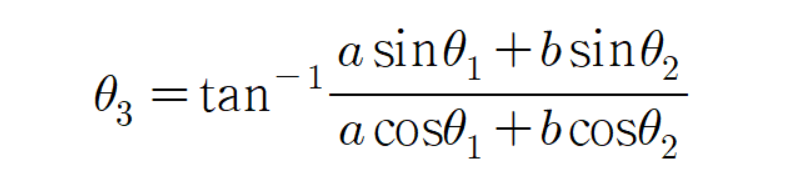
이다.
여기서

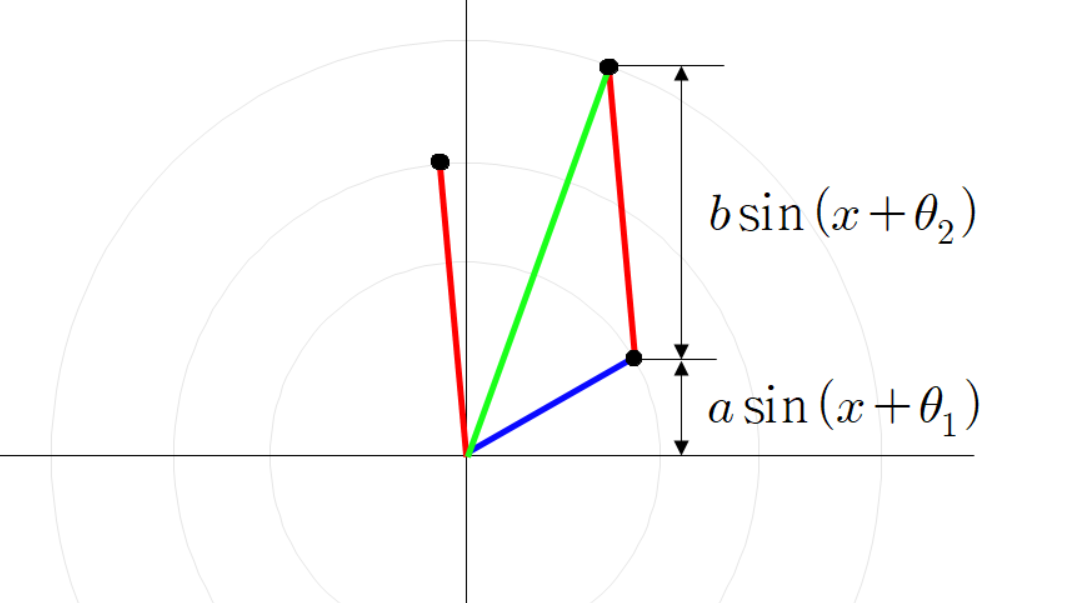
여기서 초록색 선분의 높이는 다음과 같다.
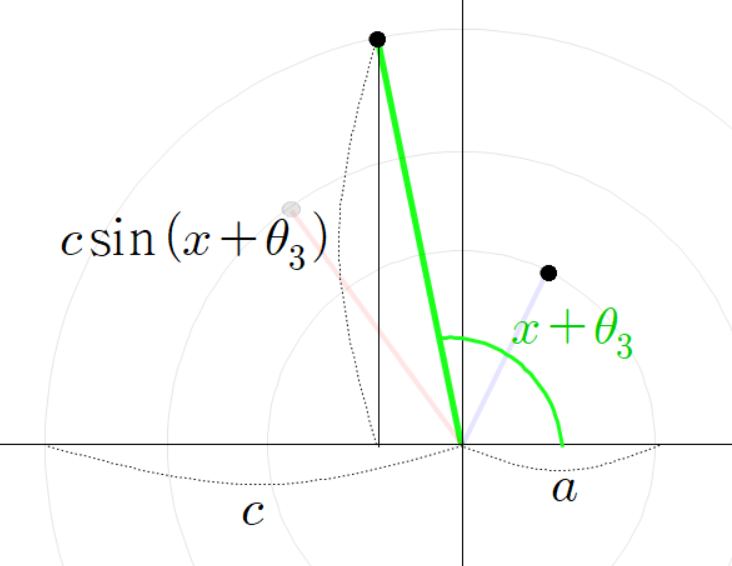
동시에 초록색 선분의 높이는 다음과 같이 계산할 수 있다.
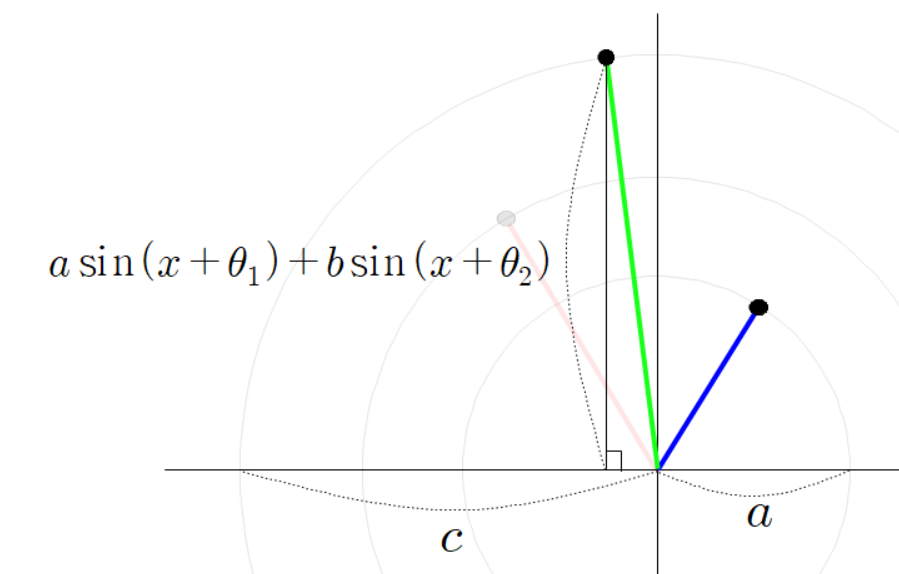
이유는 다음과 같다.
그러므로
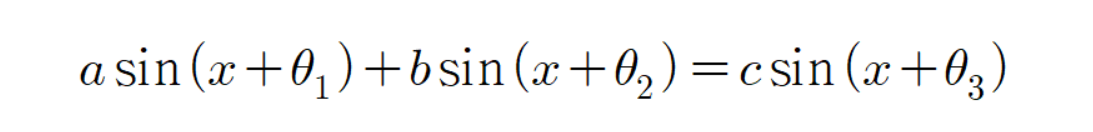
이다.
조금 전에 구한
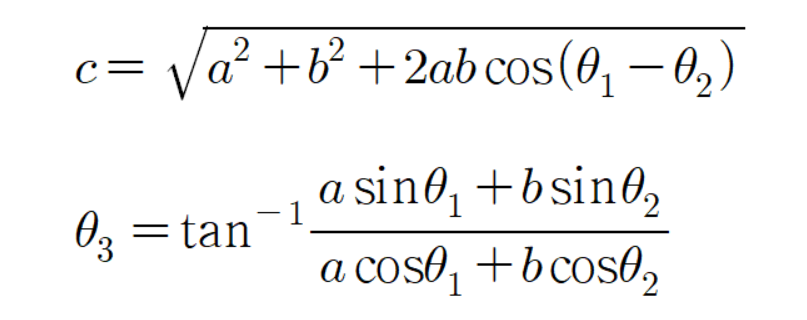
을(를) 대입하면 다음과 같은 결론이 나온다.
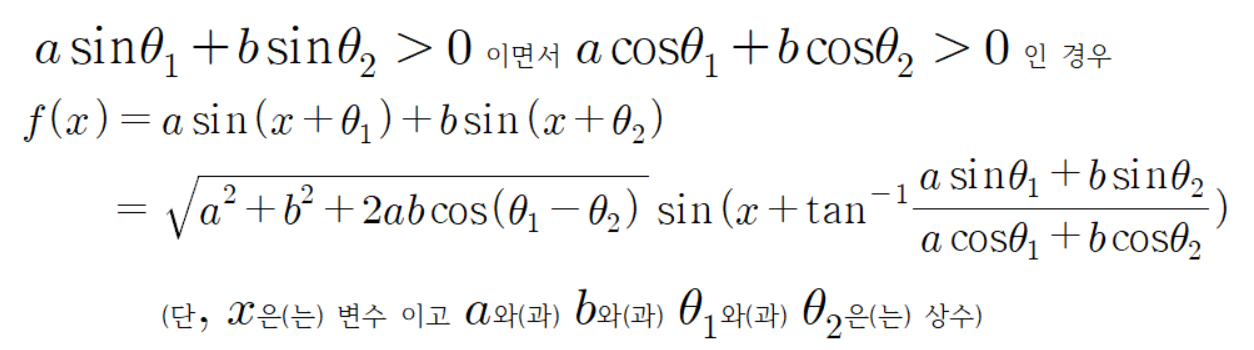
첫 번째 경우의 공식 증명이 끝났다.
이제
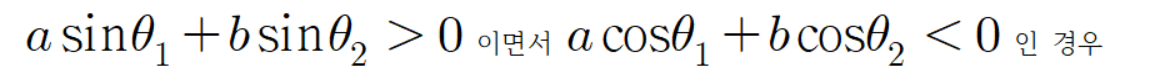
공식을 증명해 보자.
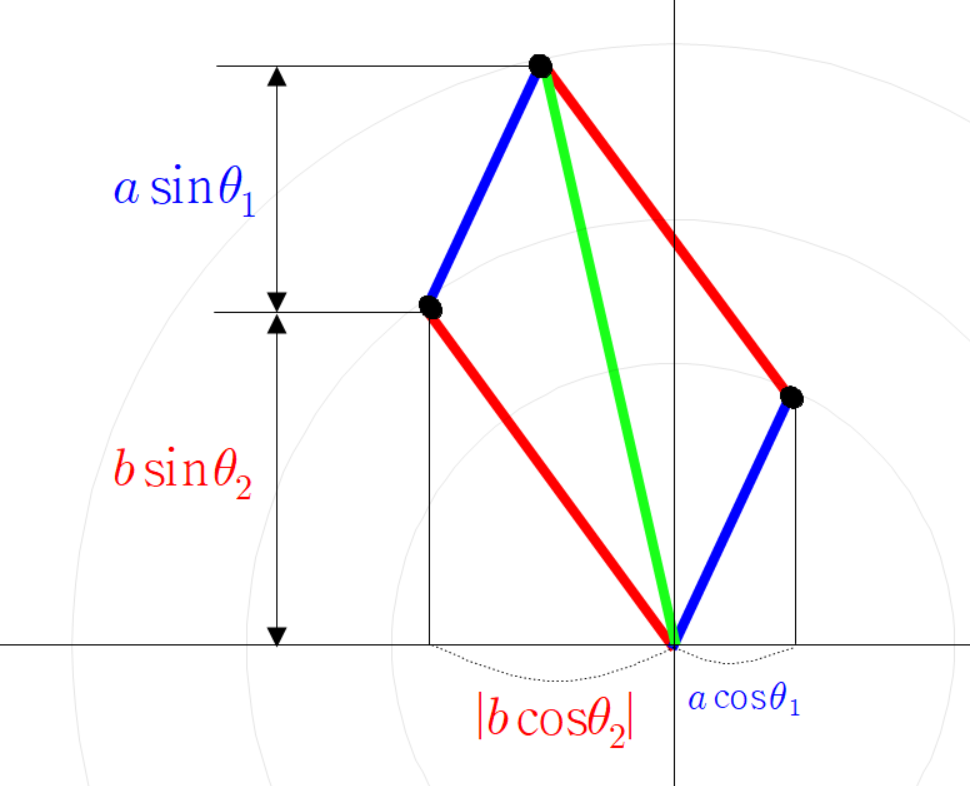
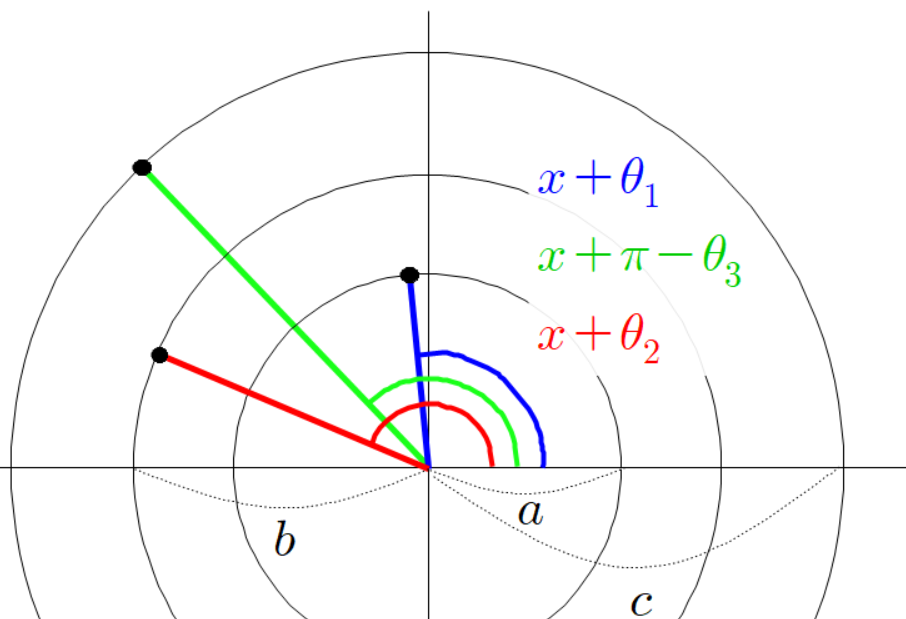
빨간 선분과 파란 선분의 각도가 다음과 같이 있다고 하자.
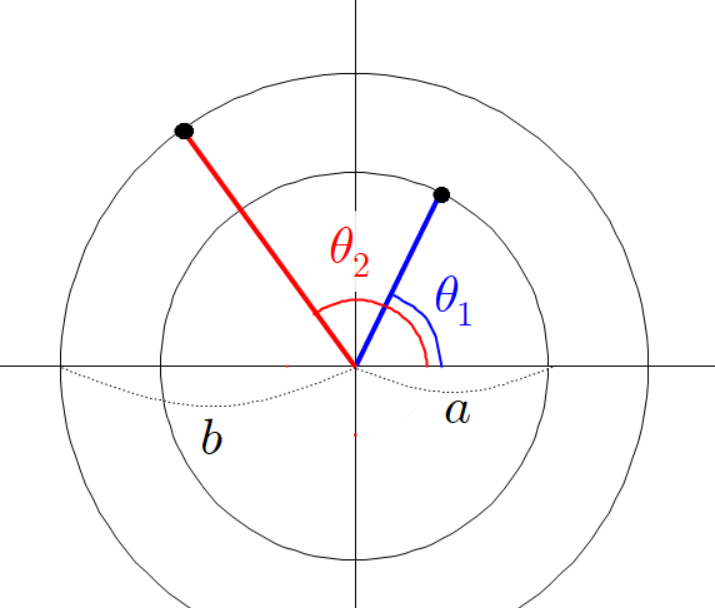
아까와 같이 평행한 두 점선을 긋고 그 점선의 교차점과 원점을 잇는 초록색 선분을 그린다.
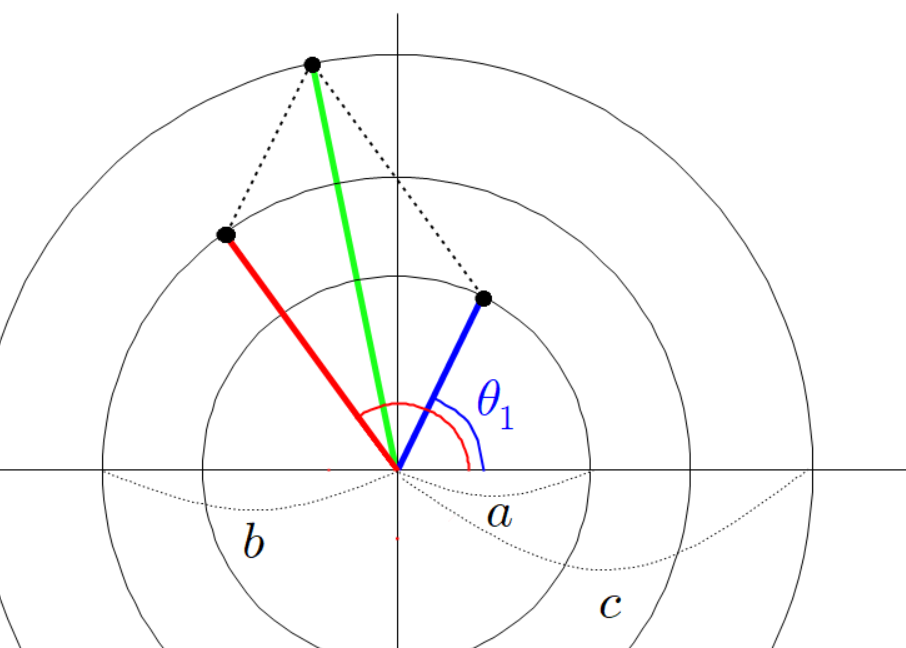

세 점들의 좌표는 다음과 같다.
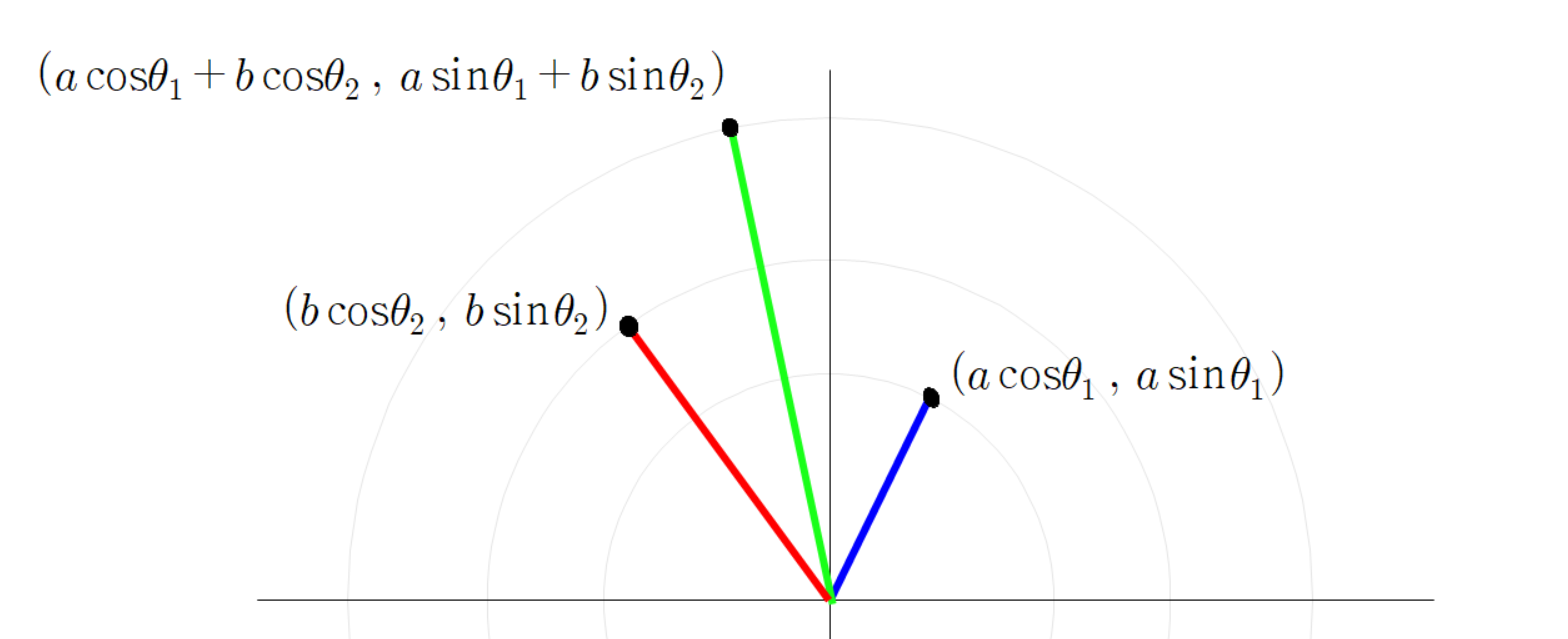
초록색 선분 끝 점의 좌표가 이렇게 계산되는 이유는
파란 선분 빨간 선분 초록 선분을 벡터로 본다면
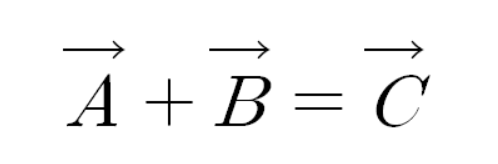
이(가) 성립하기 때문이다.
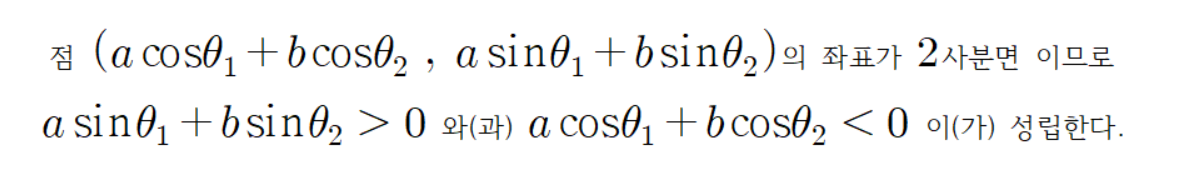
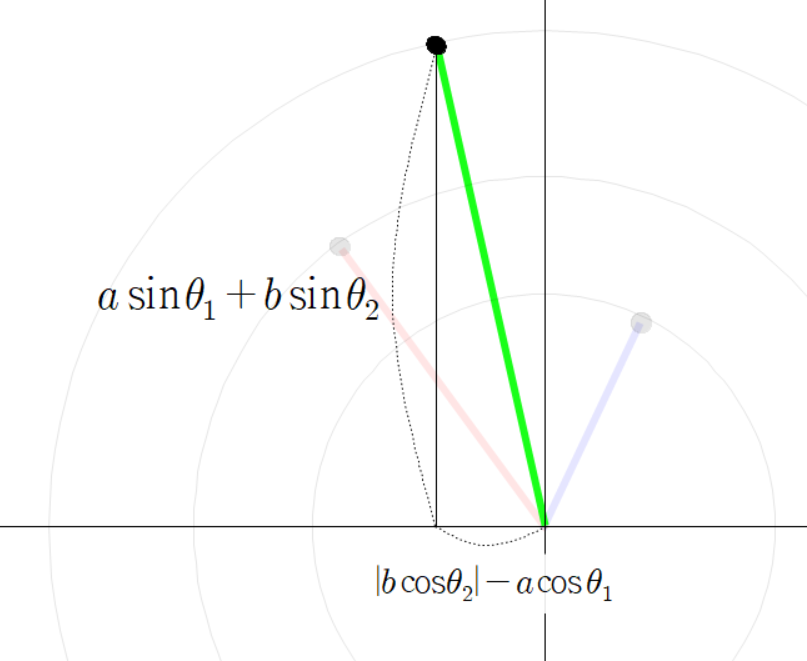
초록색 선분의 각도를 다음과 같이 정의하자.
참고로

이 각도는 다음과 같이 계산 할 수 있다.
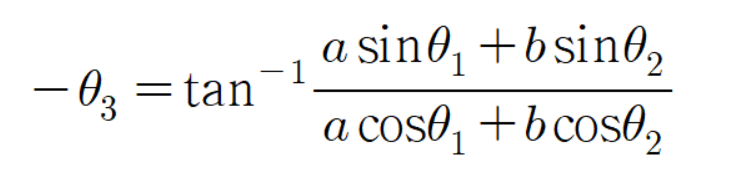
이유는 다음과 같다.
이므로
이다.
그러므로
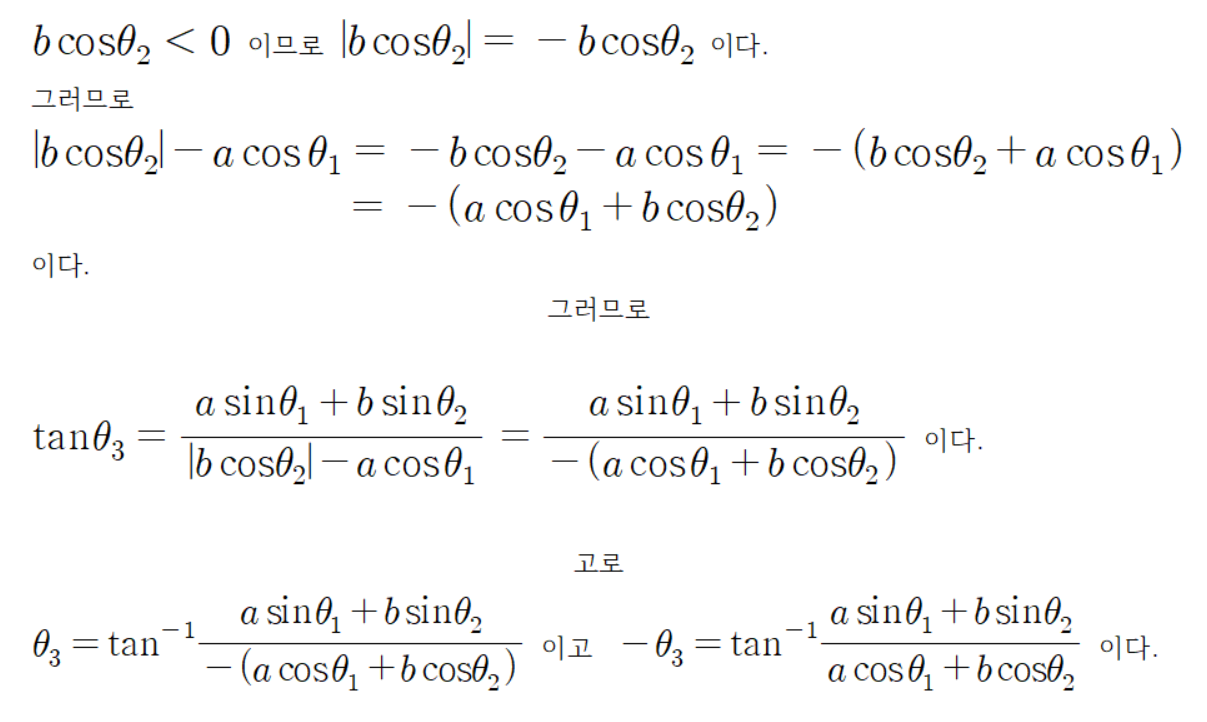
그리고 초록색 선분의 반대쪽 각은 다음과 같다.
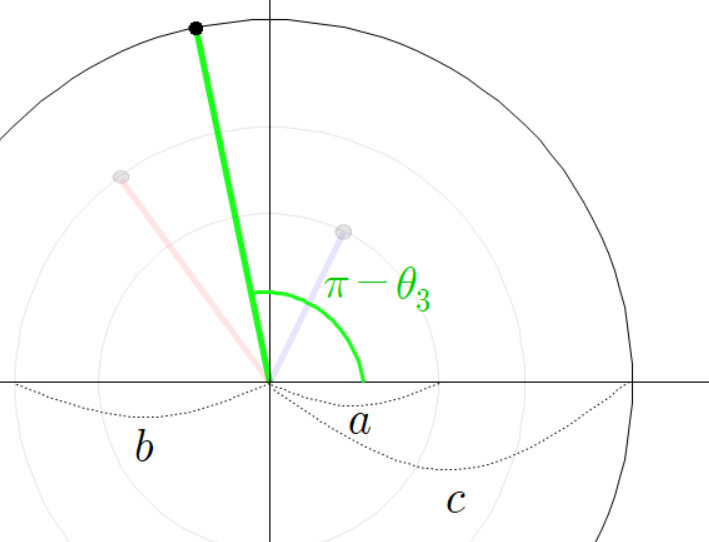
여기서

이 때 초록색 선분의 높이는 다음과 같이 나타낼 수 있다.
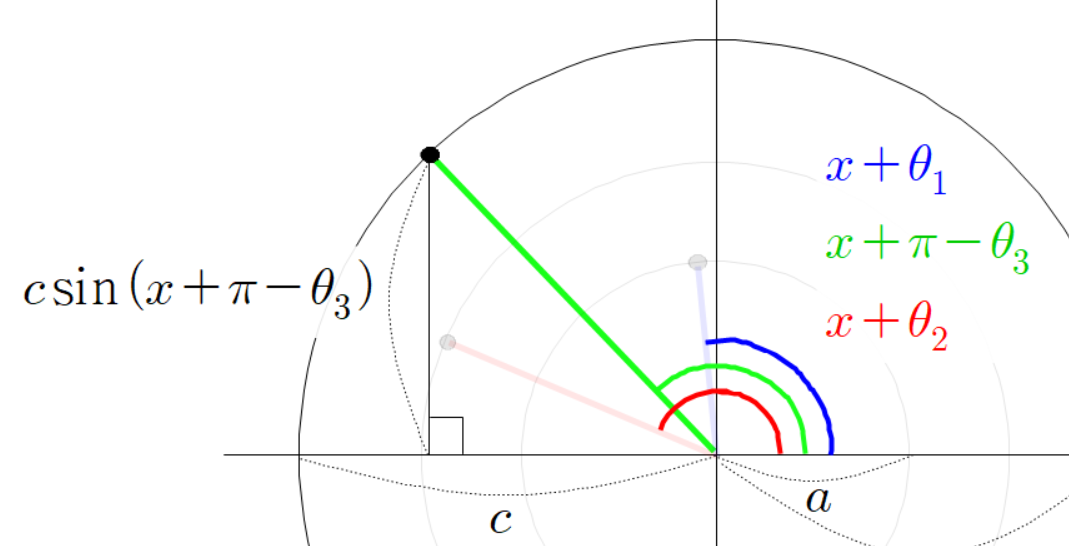
동시에 초록색 선분의 높이를 다음과 같이 계산할 수 있다.
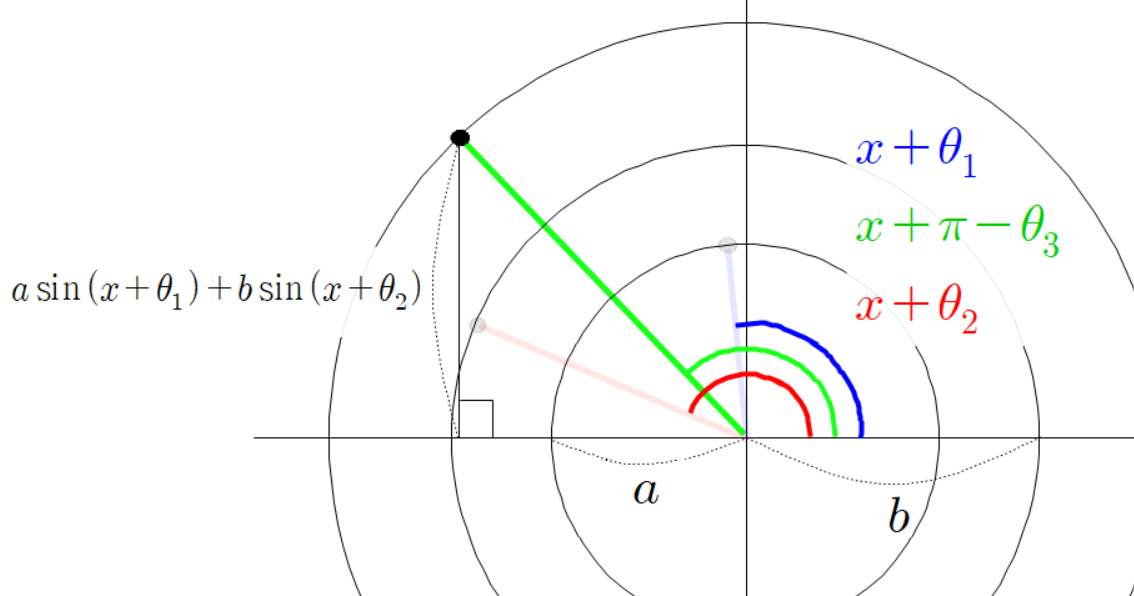
이유는 다음과 같다.
그러므로

이다.
그리고
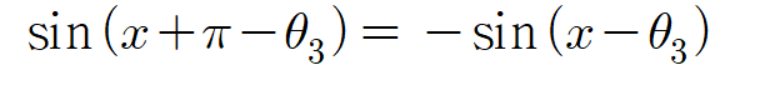
이므로
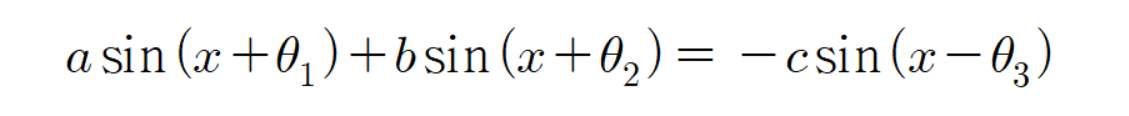
이다.
조금 전에 구한
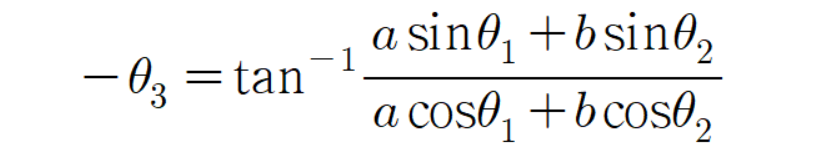
을(를) 대입하면
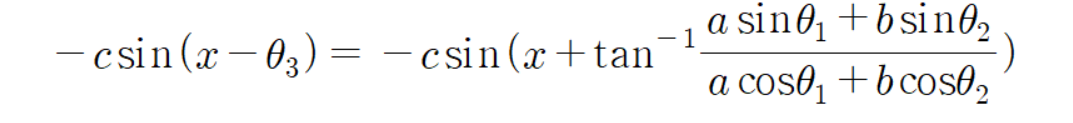
이다.

따라서 다음과 같은 결론이 나온다.
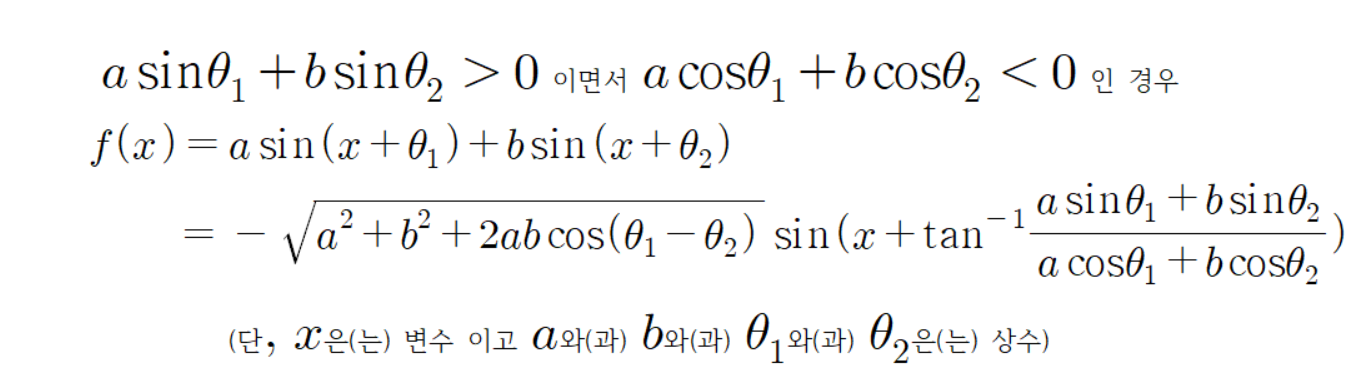
두 번째 경우의 공식 증명이 끝났다.
이제

공식을 증명해 보자.
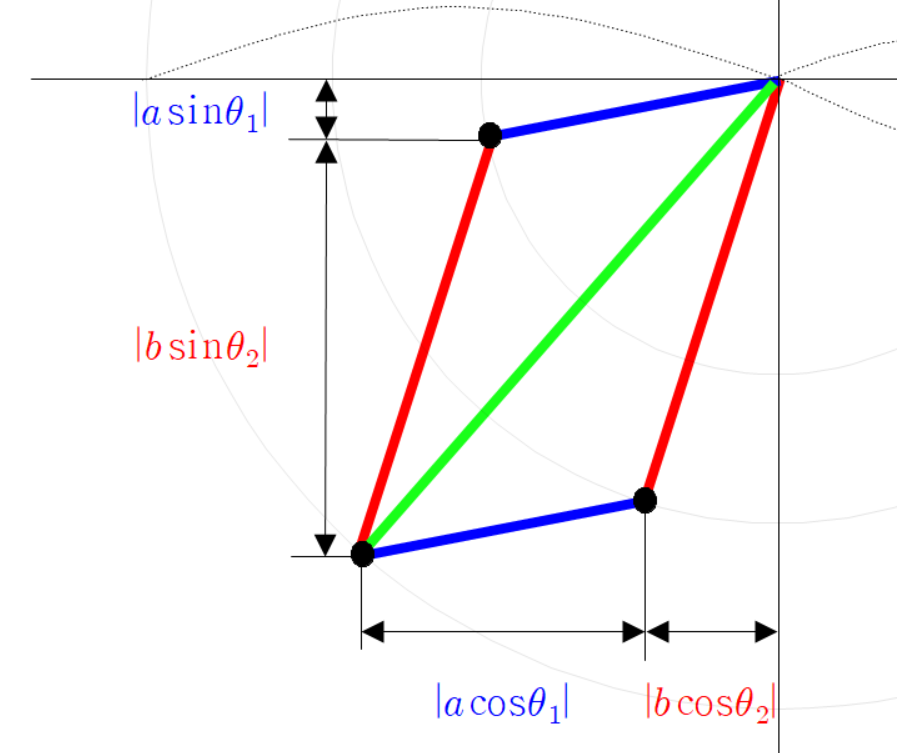
빨간 선분과 파란 선분의 각도가 다음과 같이 있다고 하자.
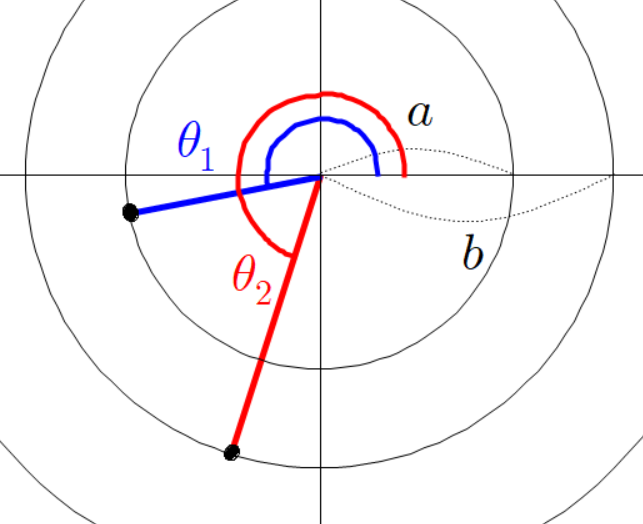
아까와 같이 평행한 두 점선을 긋고 그 점선의 교차점과 원점을 잇는 초록색 선분을 그린다.
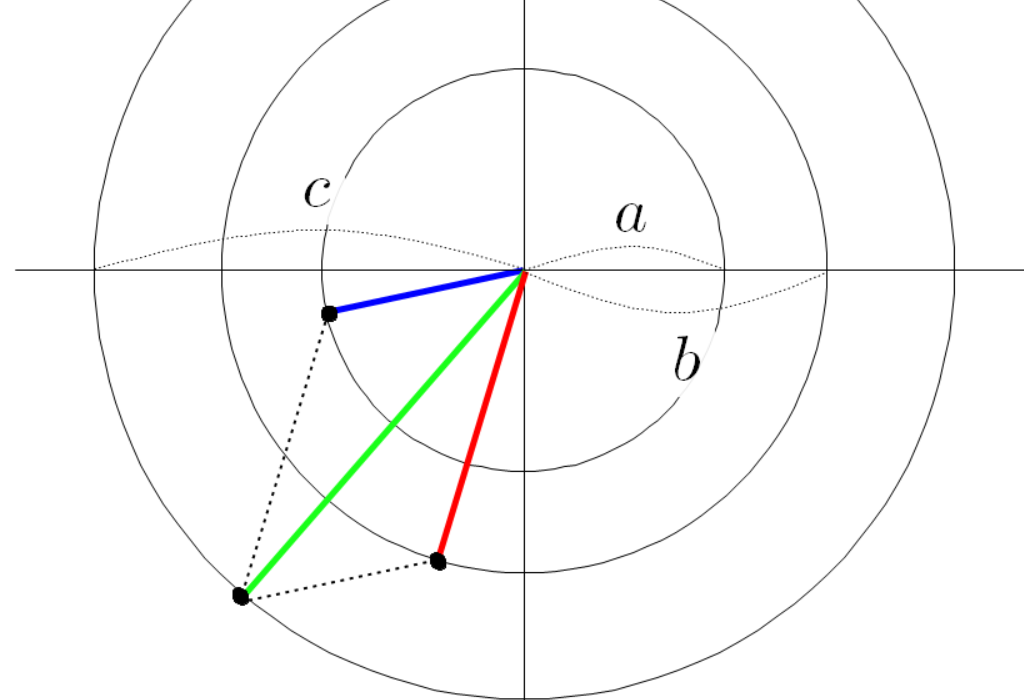

세 점의 좌표는 다음과 같다.
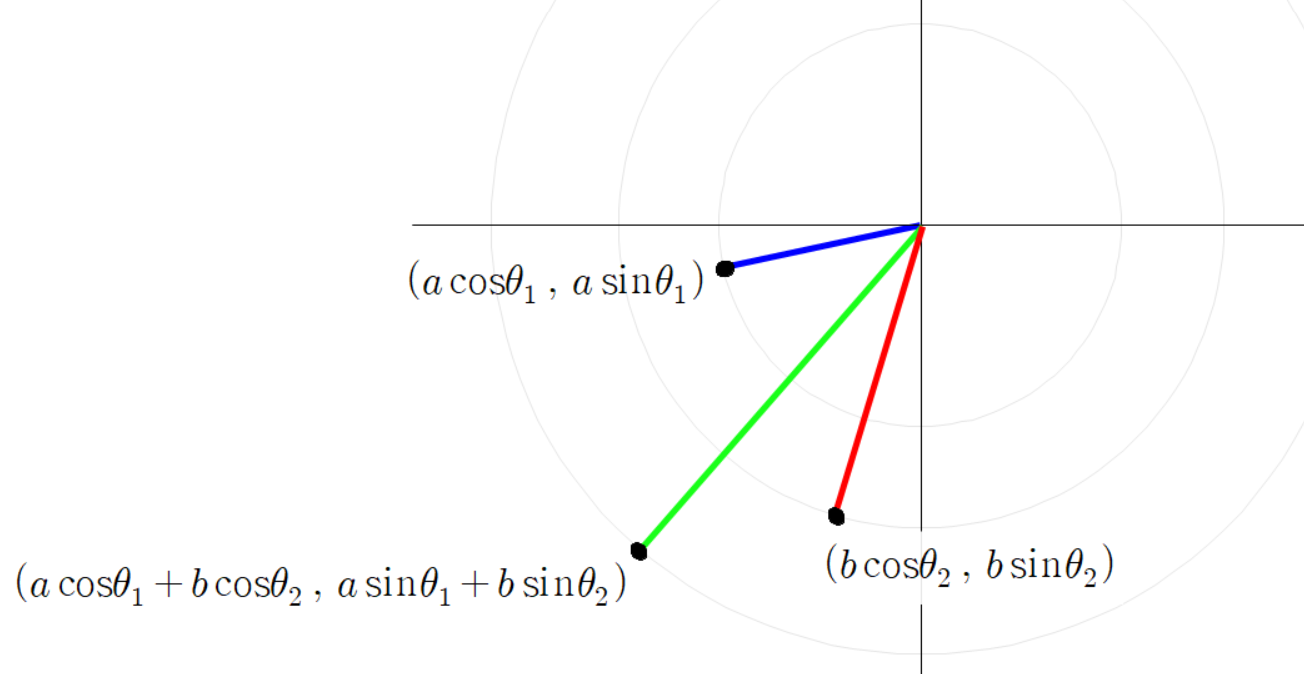
초록색 선분 끝 점의 좌표가 이렇게 계산되는 이유는
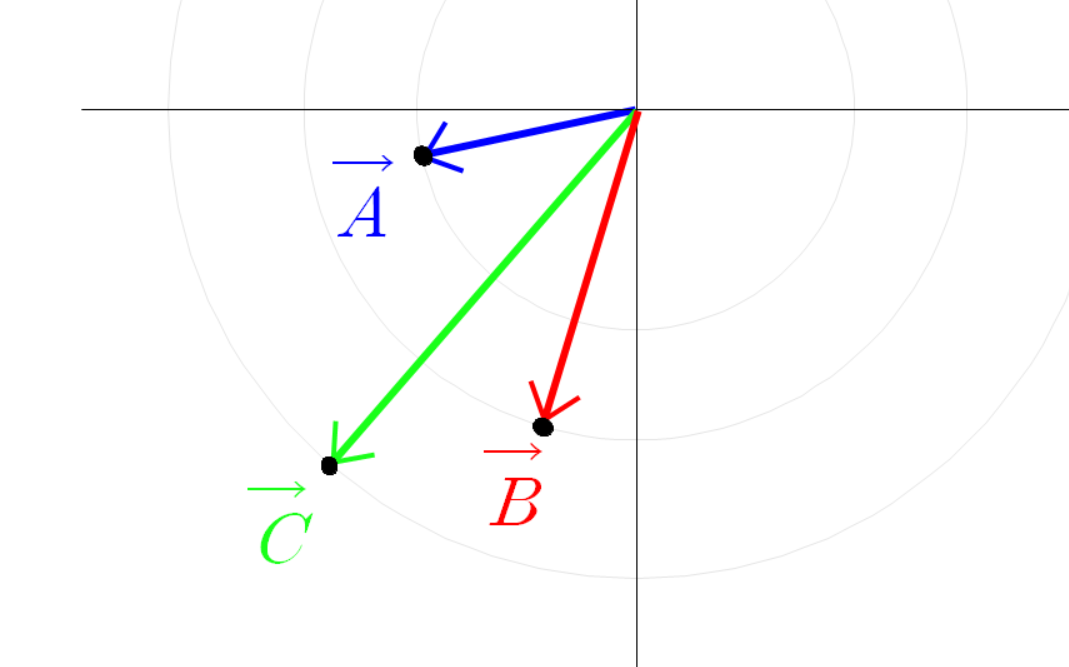
파란 선분 빨간 선분 초록 선분을 벡터로 본다면
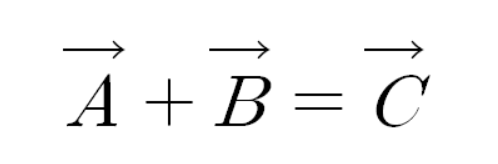
이(가) 성립하기 때문이다.
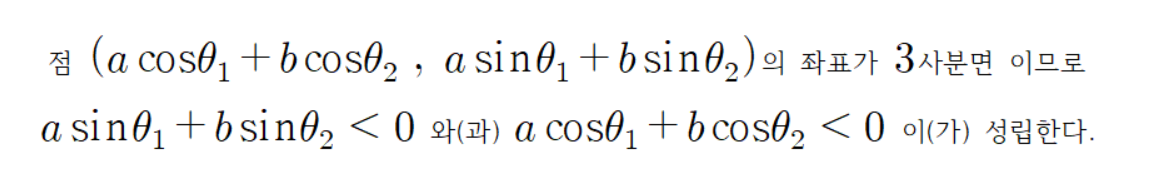
그리고 초록색 선분의 각도를 다음과 같이 정의하자.

참고로

이 각도는 다음과 같이 계산 할 수 있다.
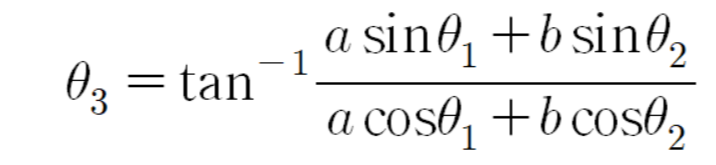
이유는 다음과 같다.
이므로
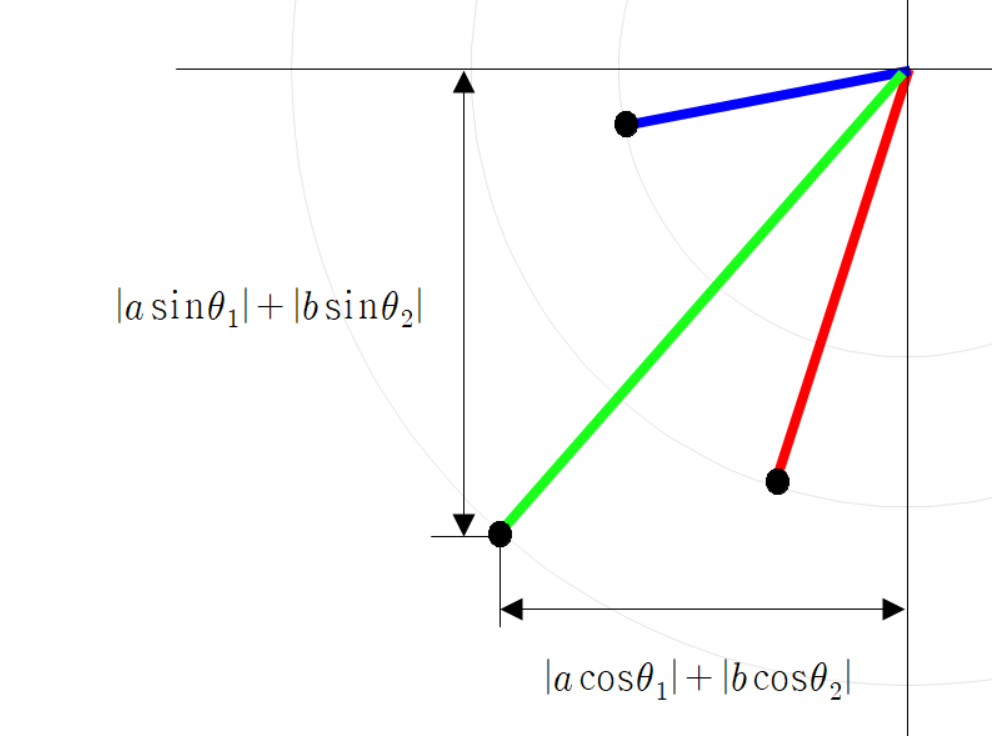
이다.
그러므로
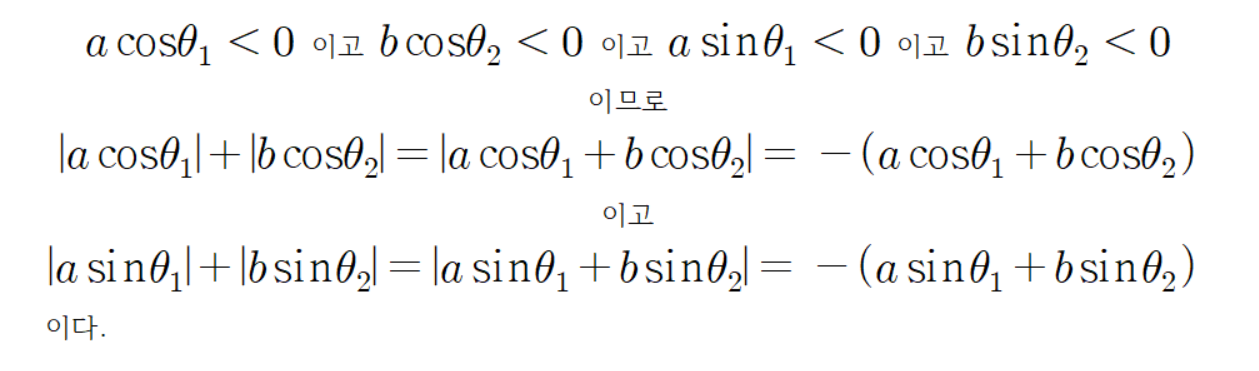
따라서
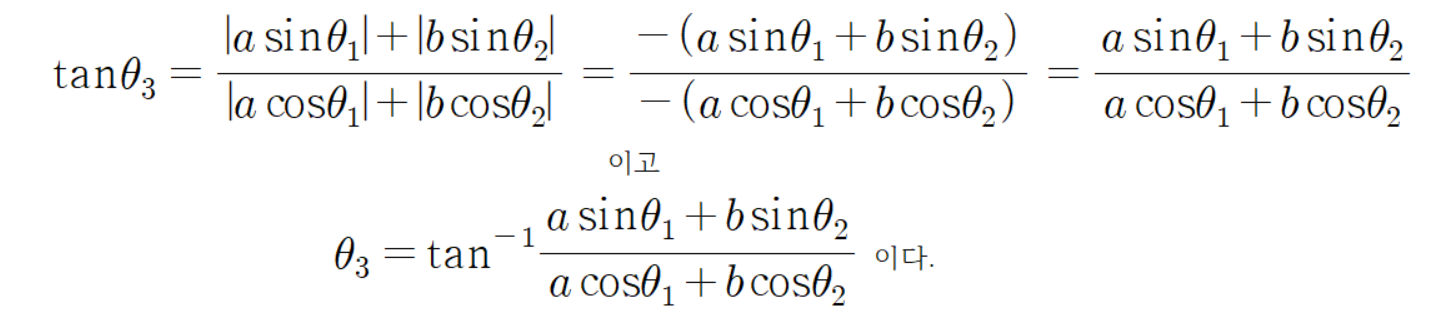
그리고 초록색 선분의 전체 각도는 다음과 같다.
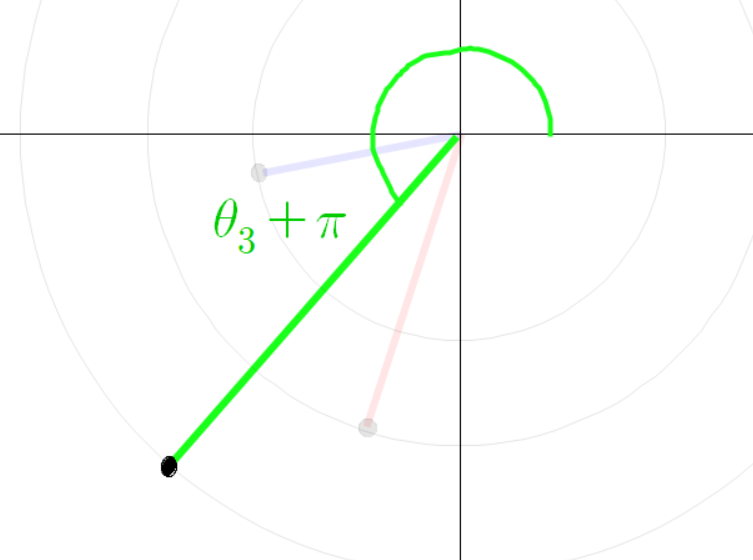
여기서

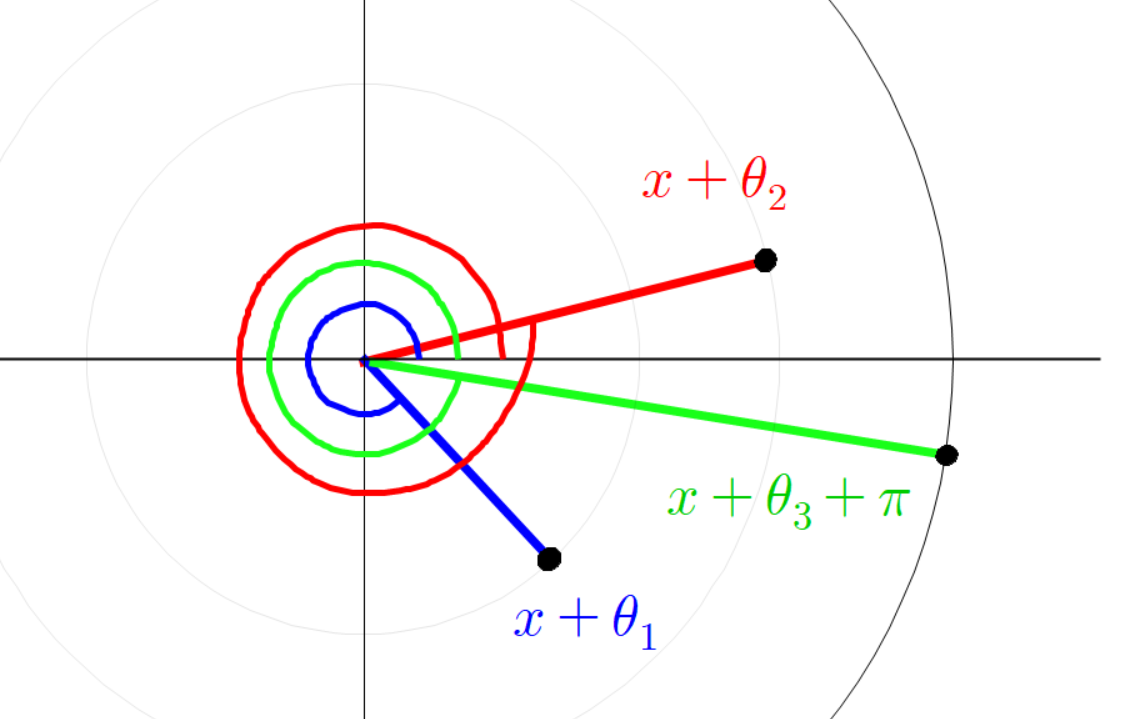
이 때 초록색 선분의 높이는 다음과 같이 나타낼 수 있다.
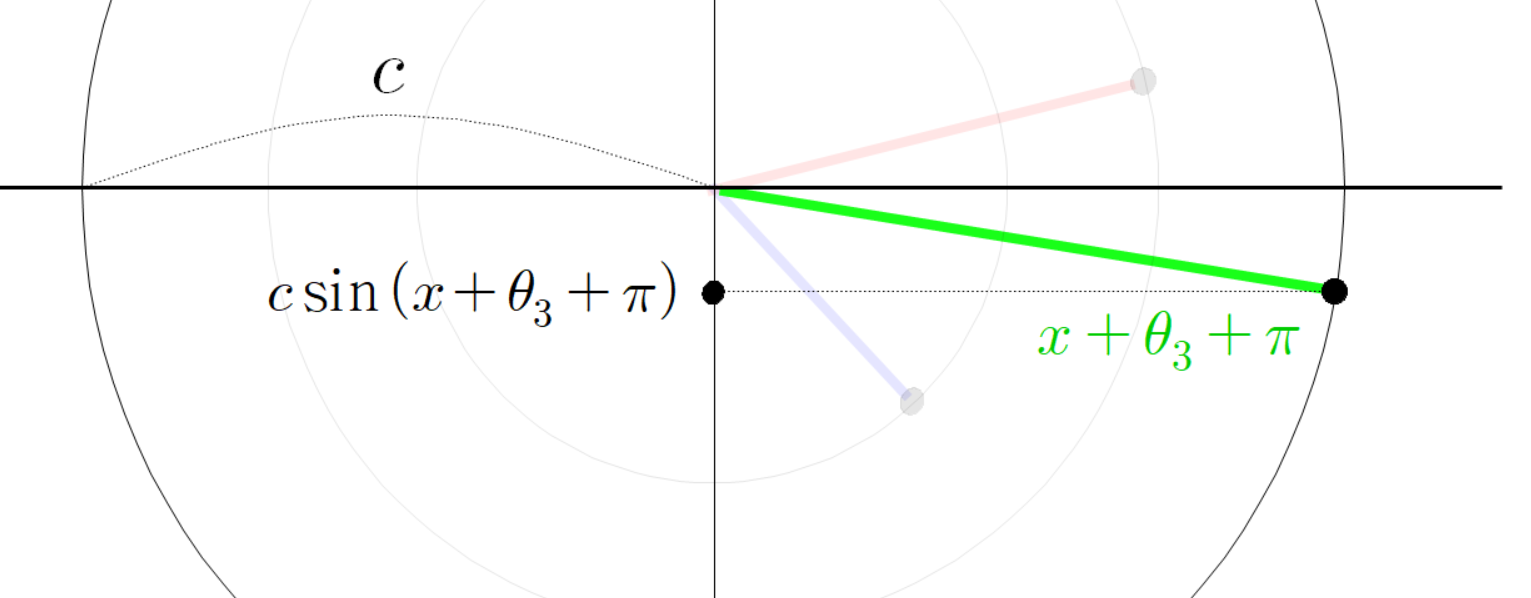
동시에 초록색 선분의 높이를 다음과 같이 계산할 수 있다.
그러므로
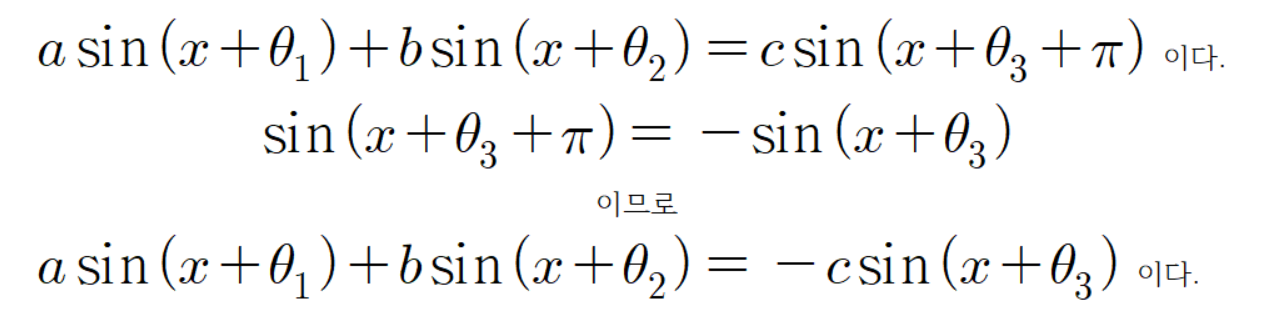
조금전에 구한
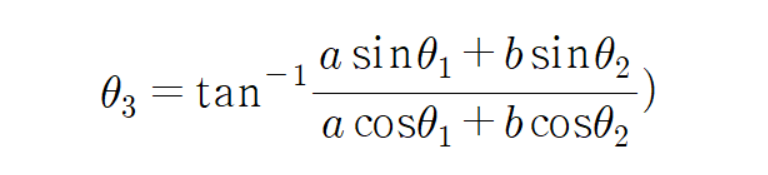
을(를) 대입하면
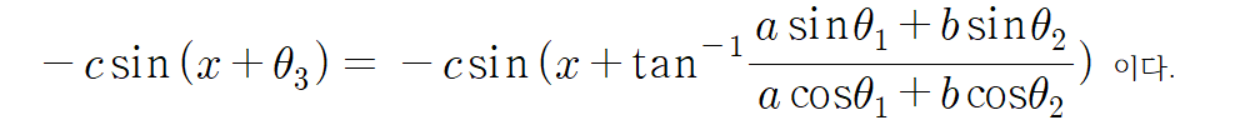

따라서 다음과 같은 결론이 나온다.
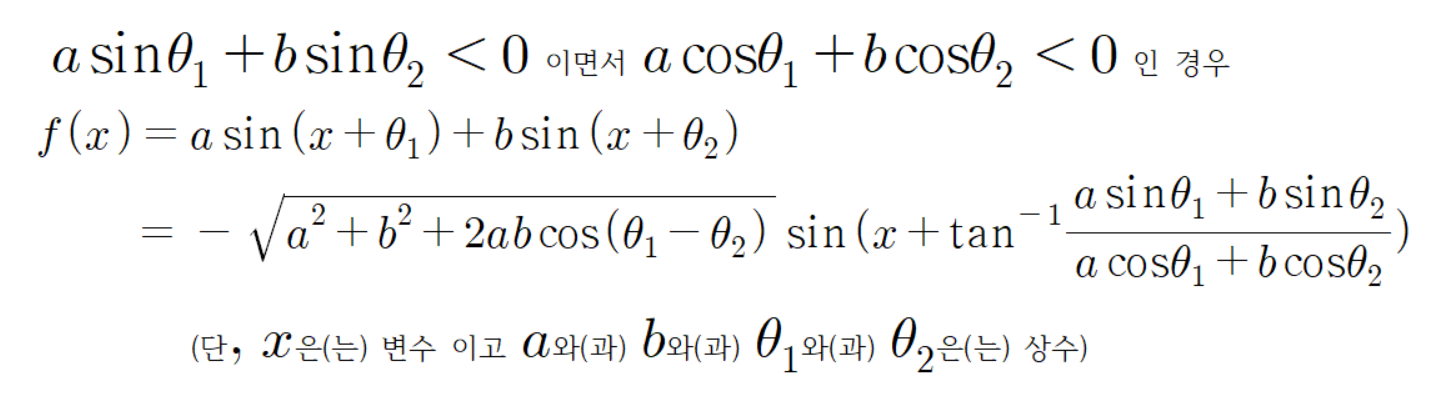
세 번째 경우의 공식 증명이 끝났다.
이제
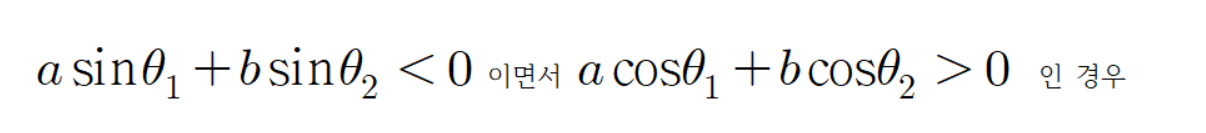
공식을 증명해 보자.
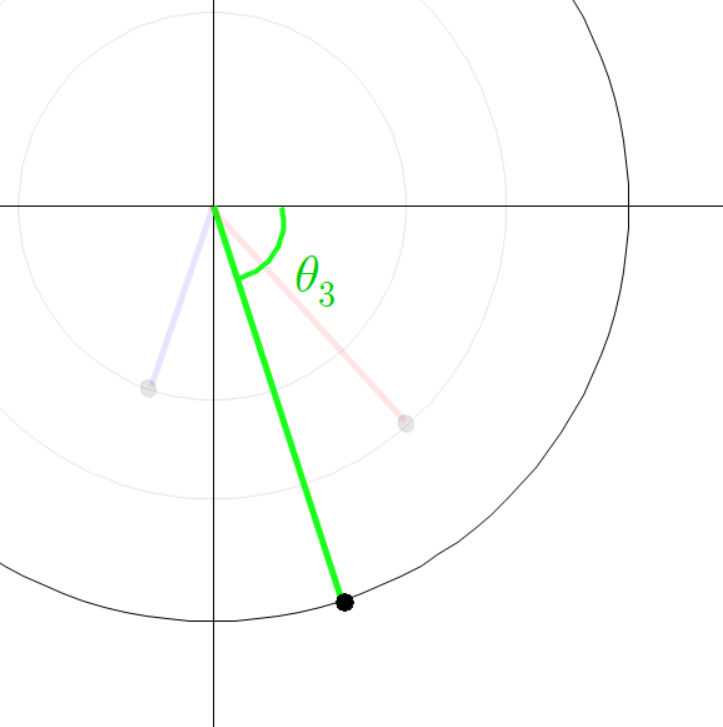
빨간 선분과 파란 선분의 각도가 다음과 같이 있다고 하자.
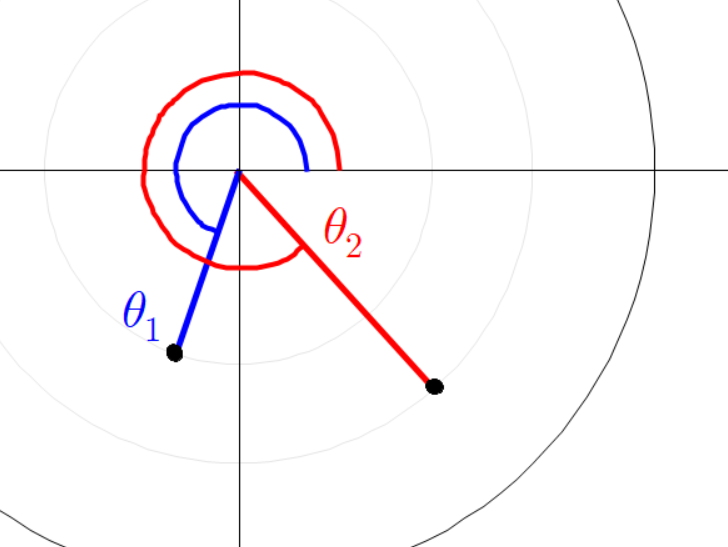
아까와 같이 평행한 두 점선을 긋고 그 점선의 교차점과 원점을 잇는 초록색 선분을 그린다.
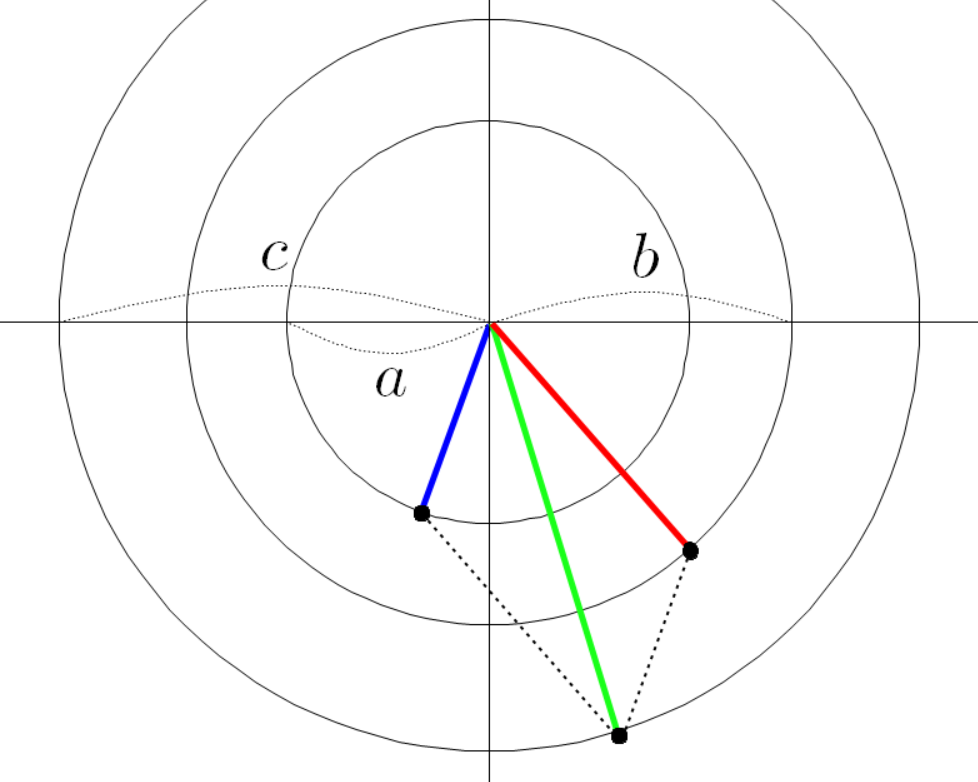

세 점의 좌표는 다음과 같다.
초록색 선분 끝 점의 좌표가 이렇게 계산되는 이유는
파란 선분 빨간 선분 초록 선분을 벡터로 본다면
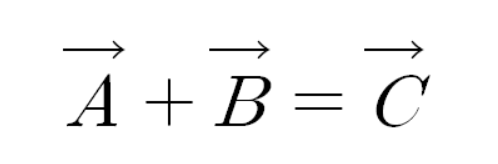
이(가) 성립하기 때문이다.
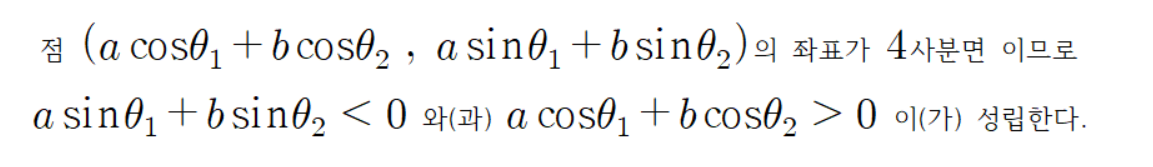
초록색 선분의 각도를 다음과 같이 정의하자.
참고로

이 각도는 다음과 같이 계산 할 수 있다.
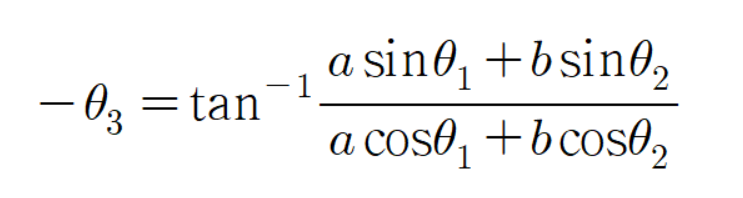
이유는 다음과 같다.
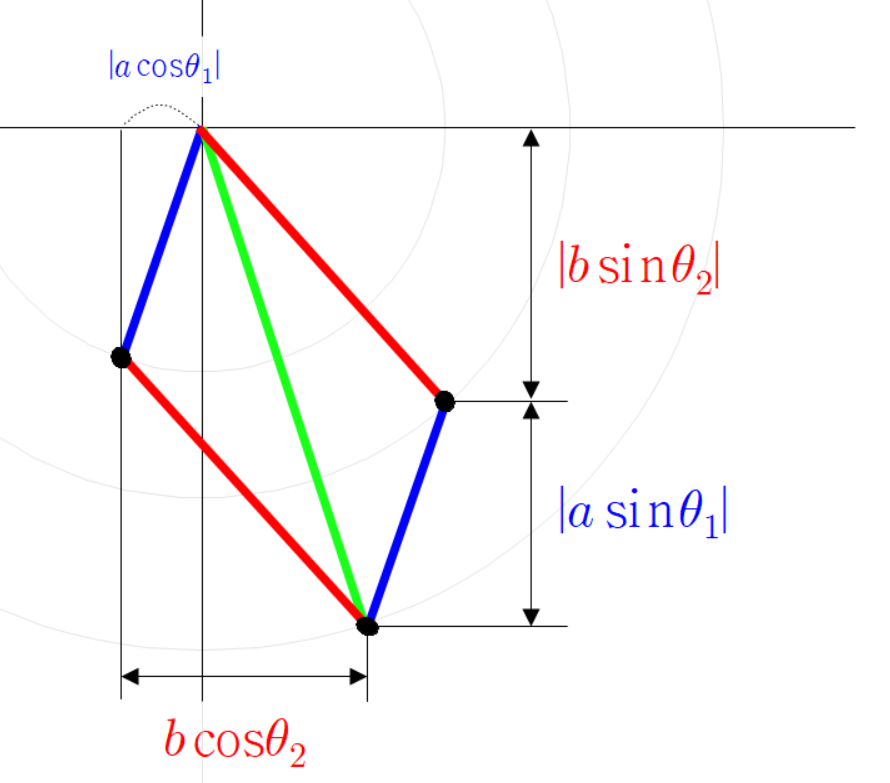
이므로
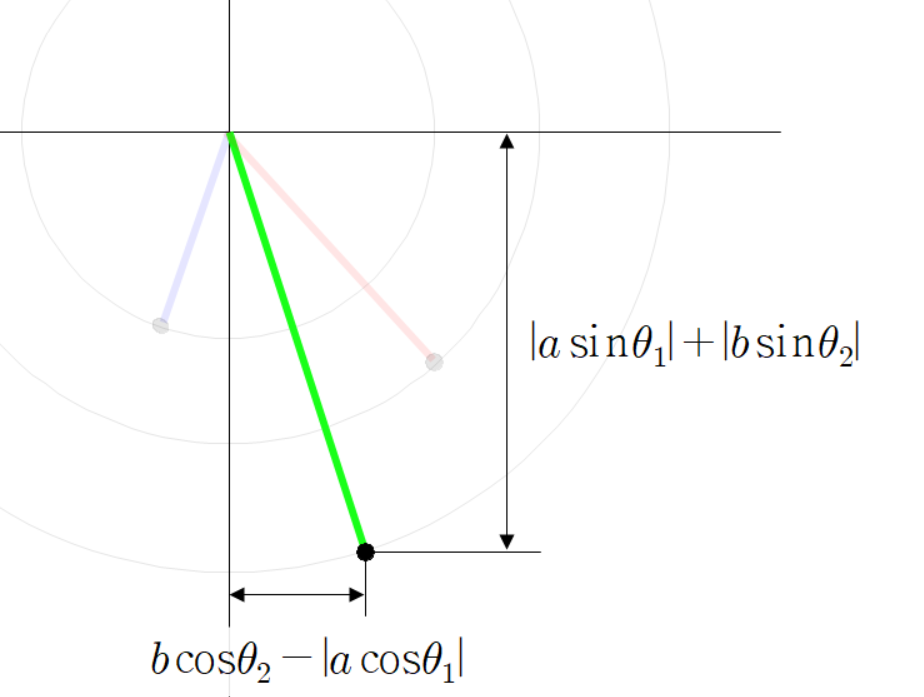
이다.
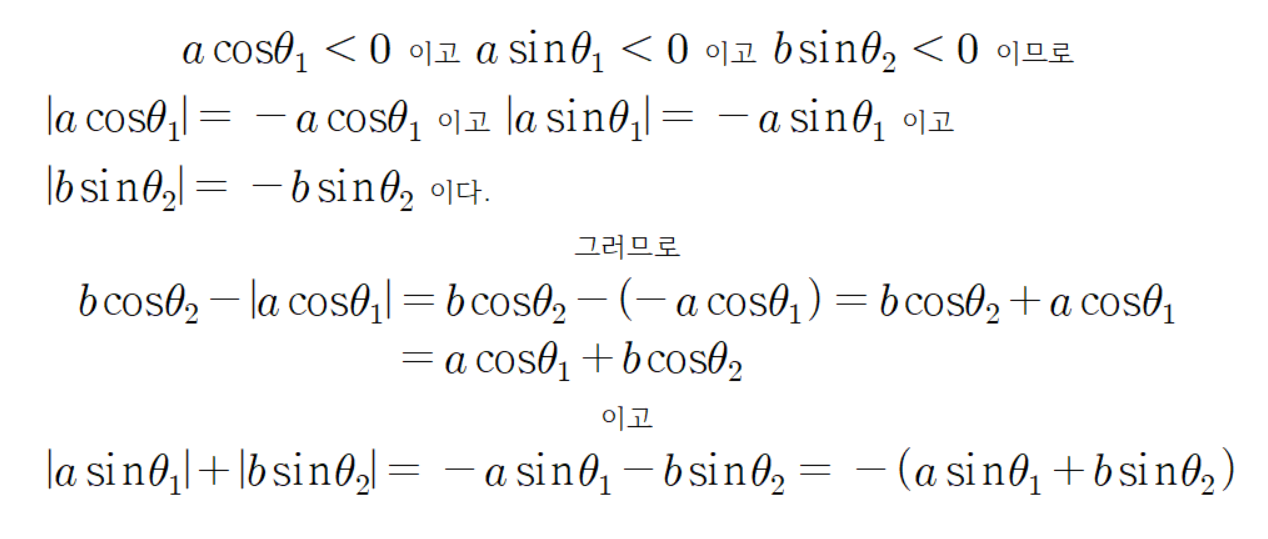
이다.
따라서
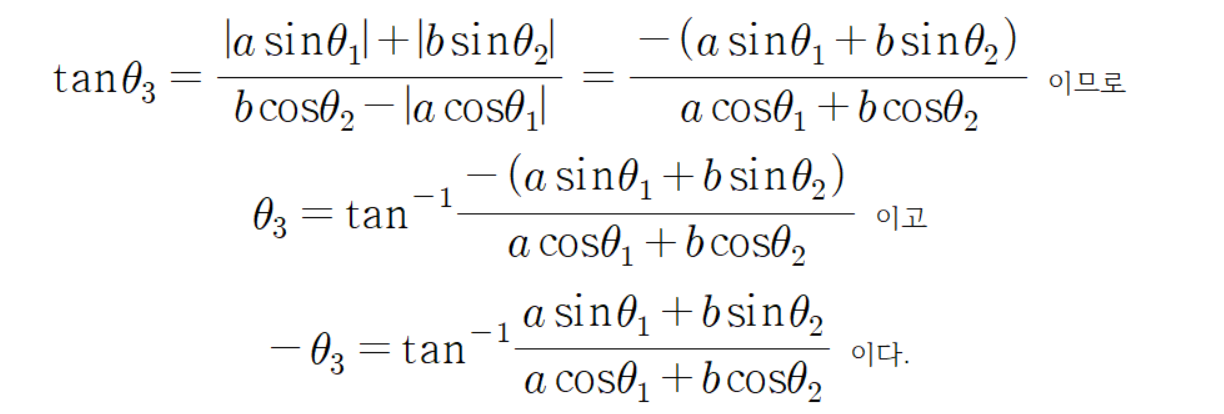
그리고 초록색 선분의 전체 각도는 다음과 같다.
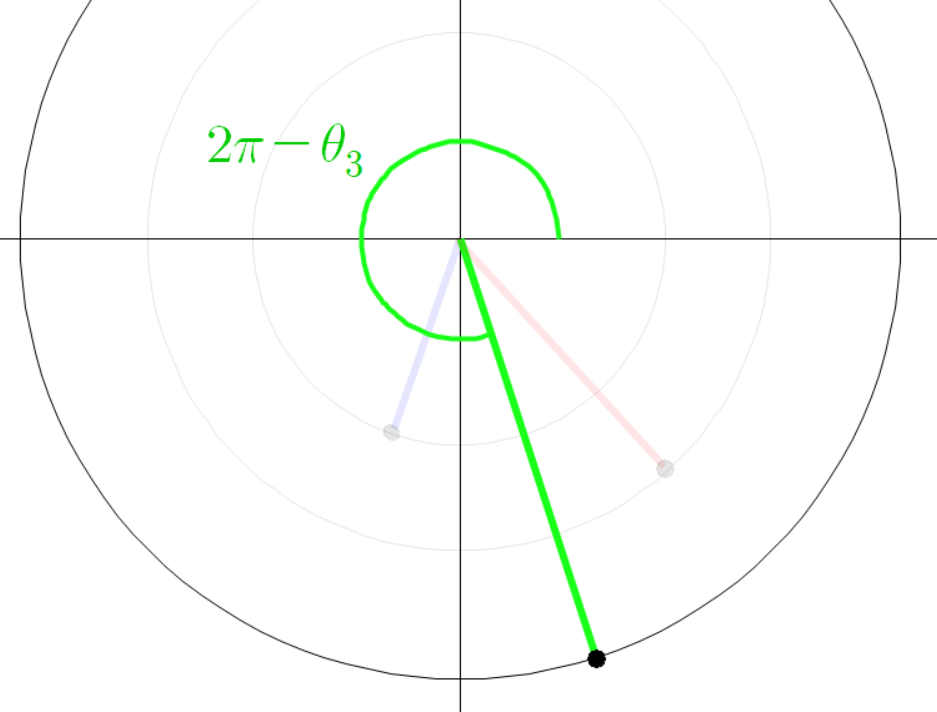
여기서

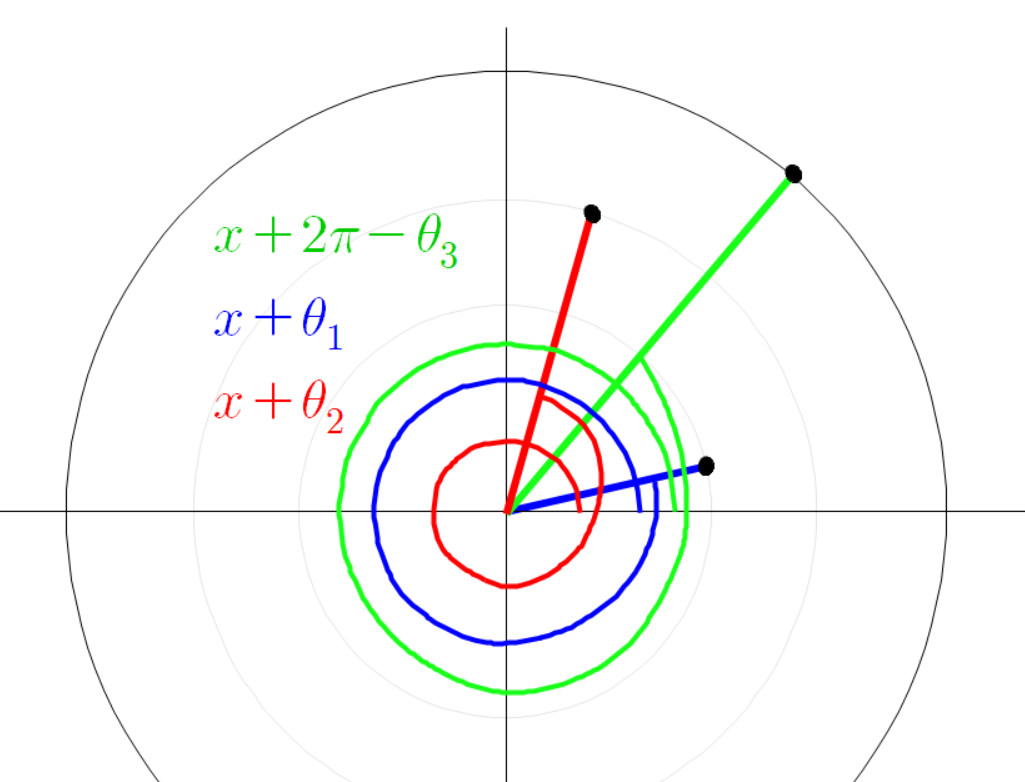
이때 초록색 선분의 높이는 다음과 같이 나타낼 수 있다.
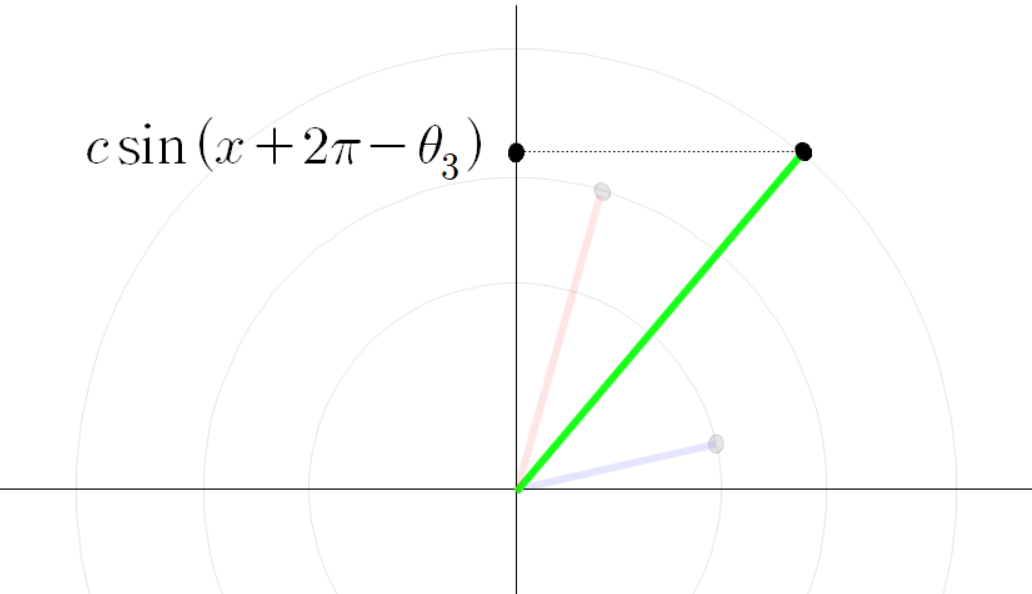
동시에 초록색 선분의 높이를 다음과 같이 계산할 수 있다.
그러므로
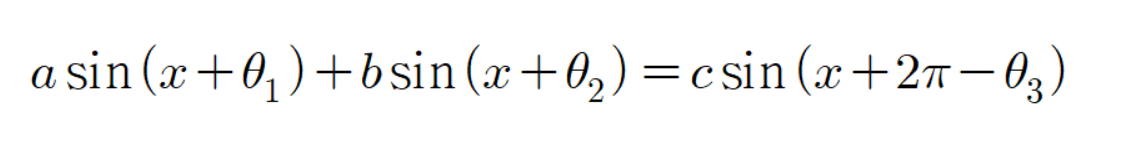
이다.
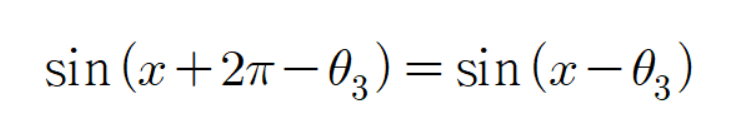
이므로
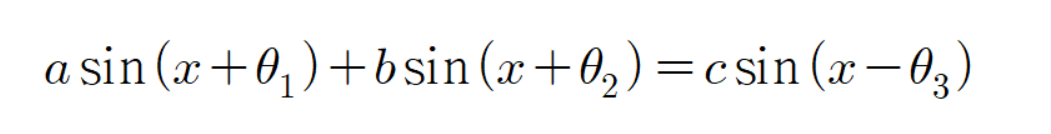
이다.
조금 전에 구한
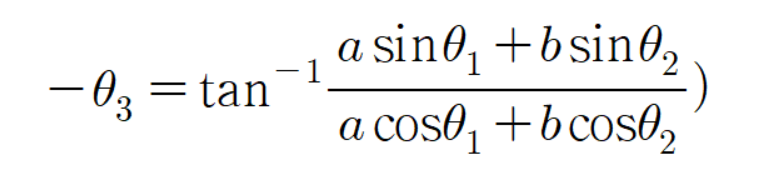
을(를) 대입하면
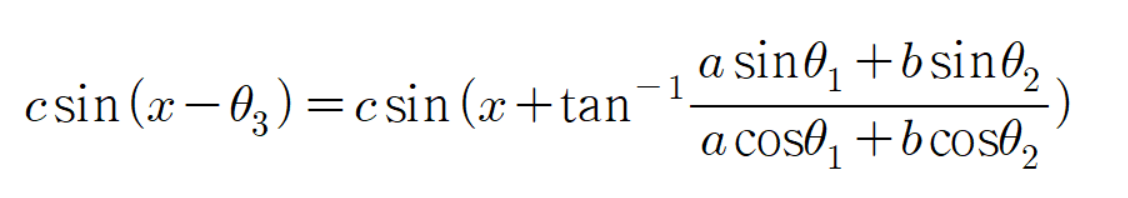
이다.

따라서 다음과 같은 결론이 나온다.
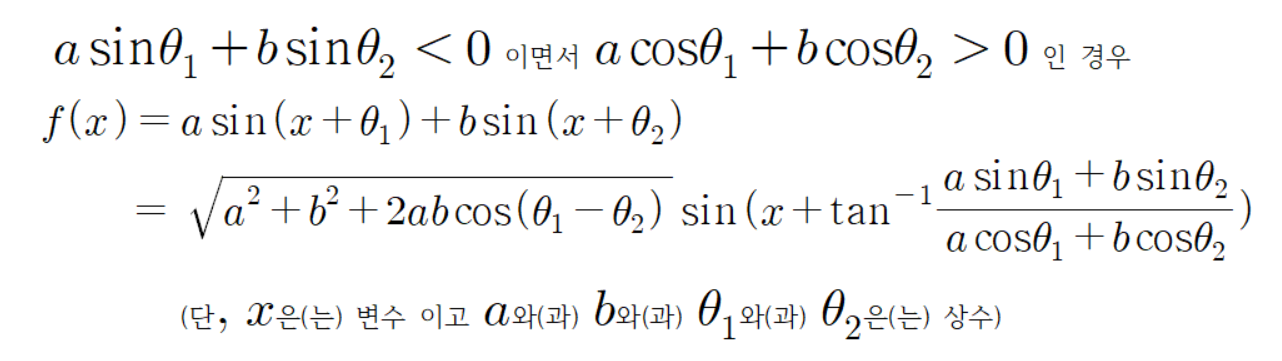
네 번째 경우의 공식 증명이 끝났다.
이제
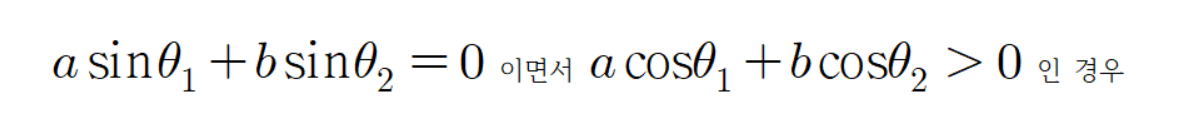
공식을 증명해 보자.
빨간 선분과 파란 선분의 각도가 다음과 같이 있다고 하자.
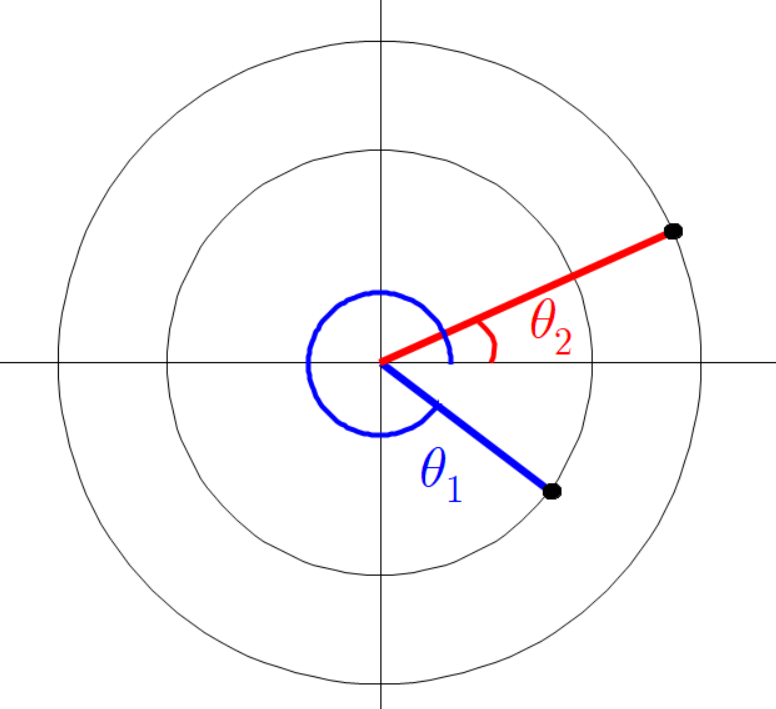
아까와 같이 평행한 두 점선을 긋고 그 점선의 교차점과 원점을 잇는 초록색 선분을 그린다.
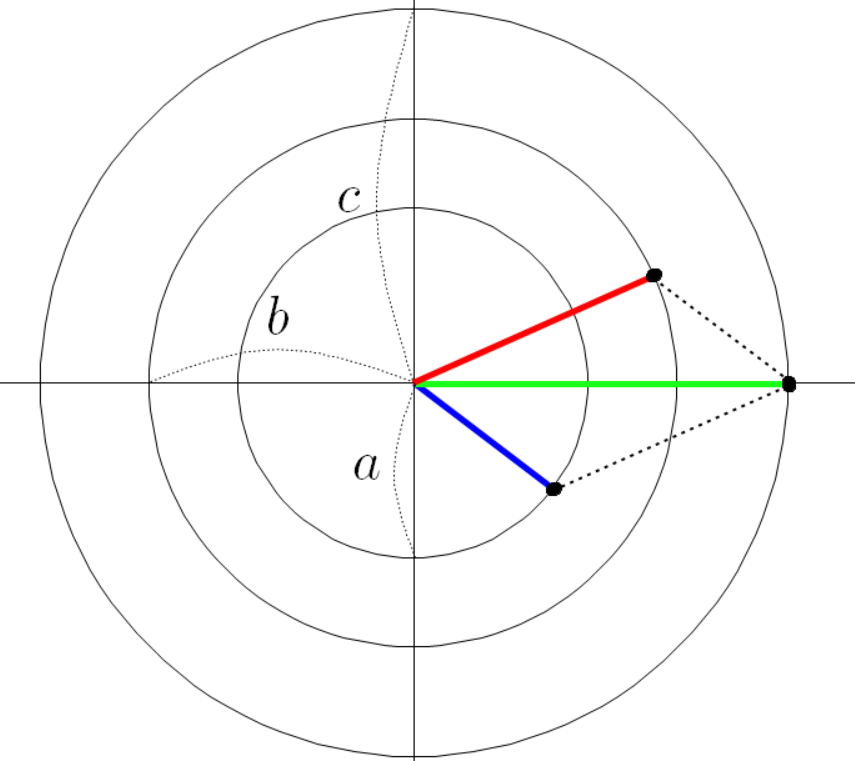

세 점의 좌표는 다음과 같다.
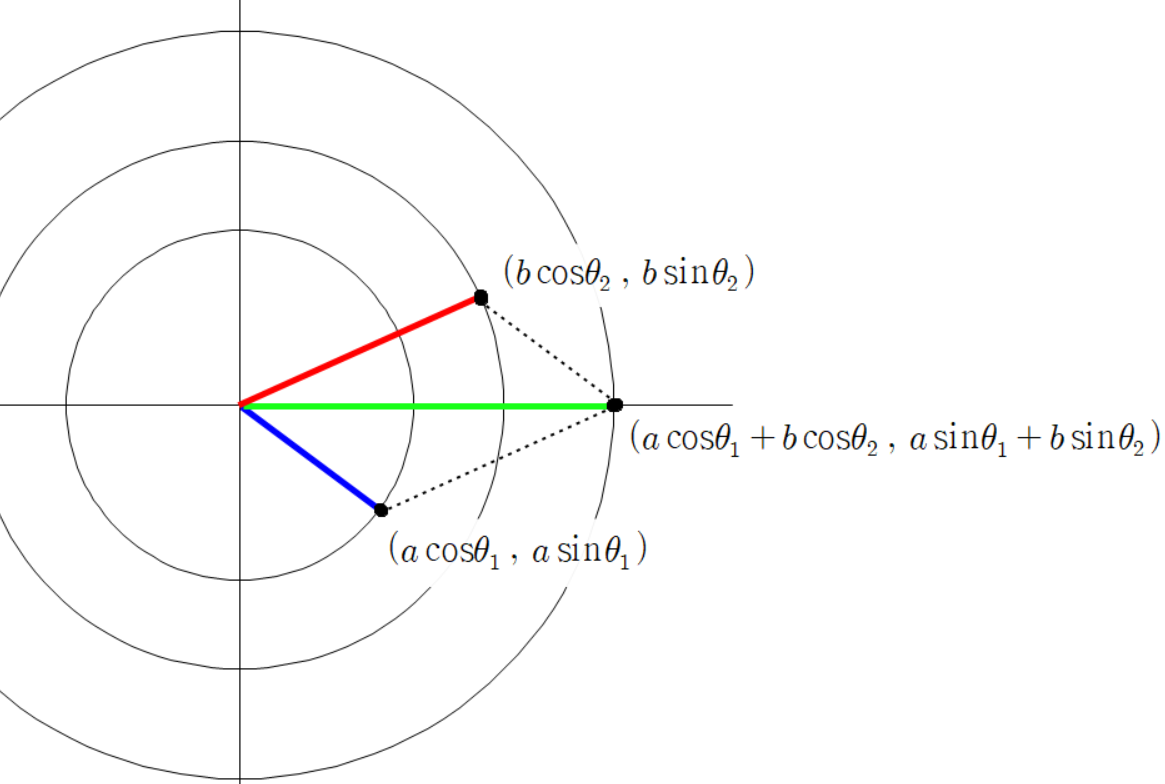
초록색 선분 끝 점의 좌표가 이렇게 계산되는 이유는
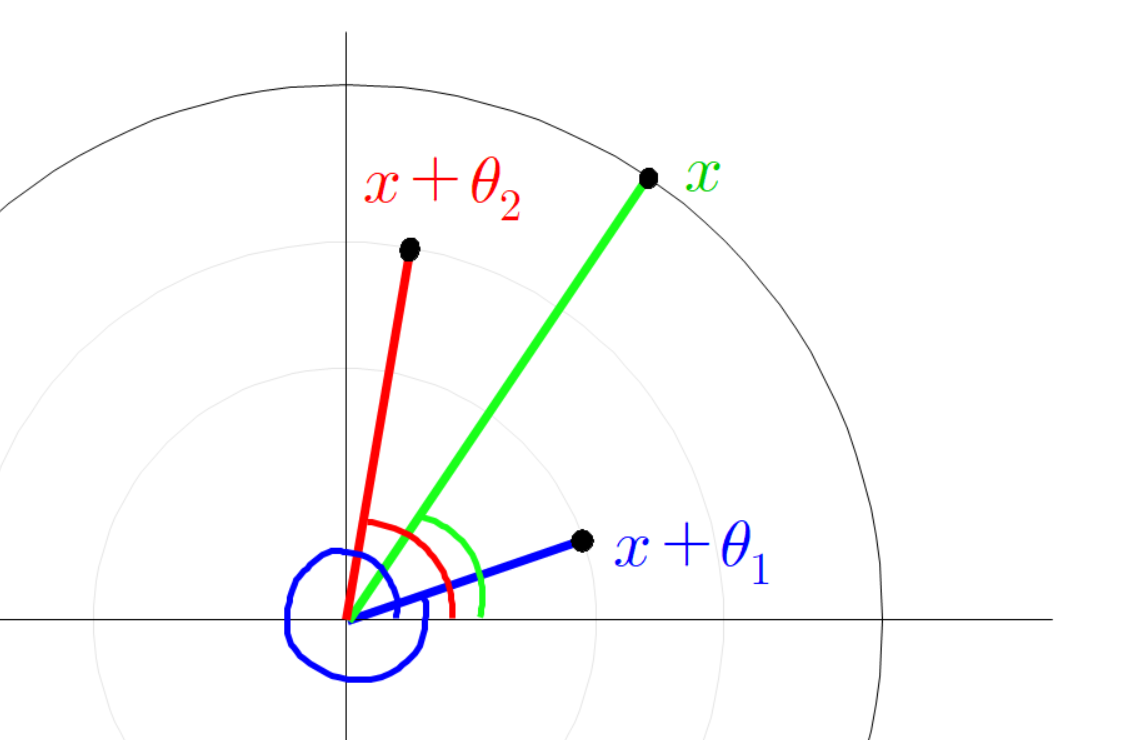
파란 선분 빨간 선분 초록 선분을 벡터로 본다면
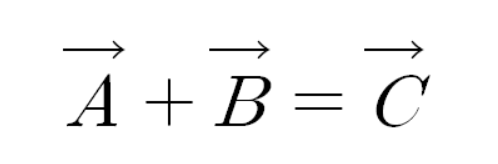
이(가) 성립하기 때문이다.

여기서

이때 초록색 선분의 높이는 다음과 같이 나타낼 수 있다.
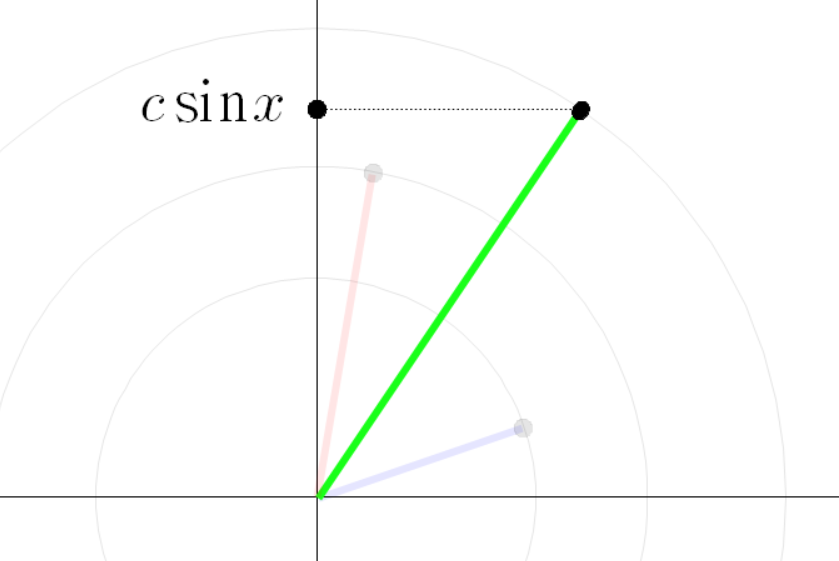
동시에 초록색 선분의 높이를 다음과 같이 계산할 수 있다.
이유는 다음과 같다.
그러므로
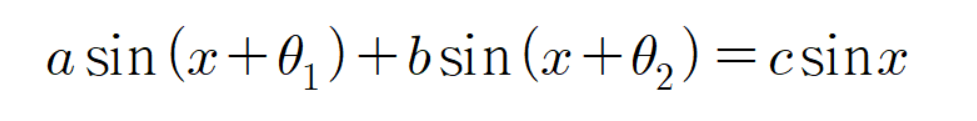
이다.

따라서 다음과 같은 결론이 나온다.
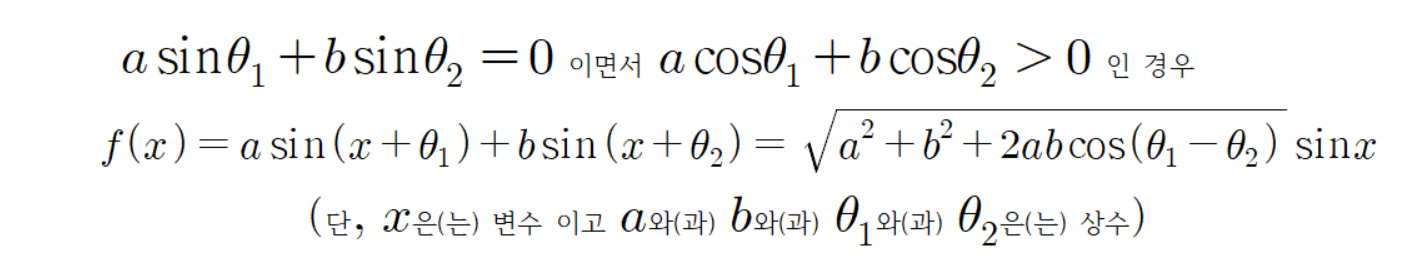
이제
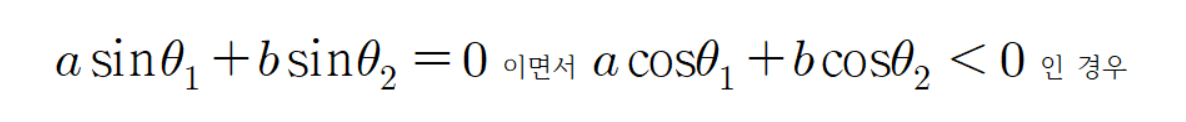
공식을 증명해 보자.
빨간 선분과 파란 선분의 각도가 다음과 같이 있다고 하자.
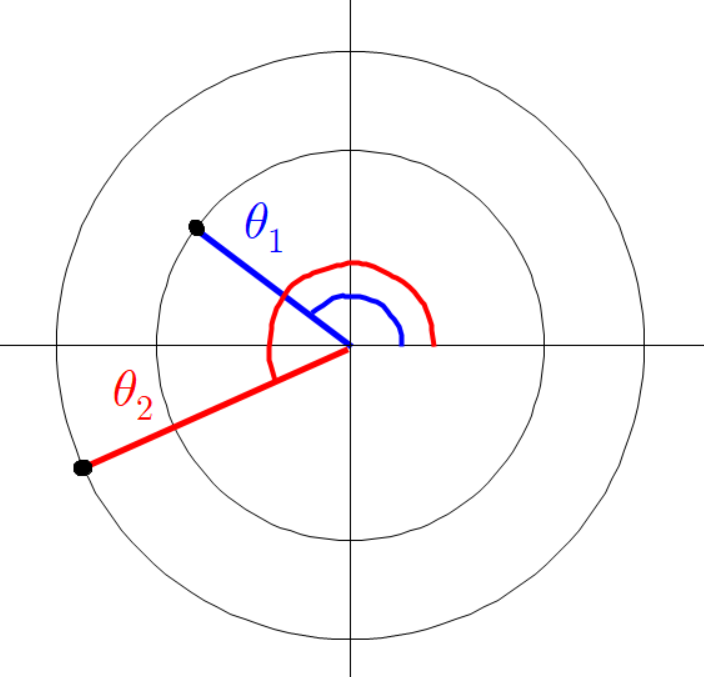
아까와 같이 평행한 두 점선을 긋고 그 점선의 교차점과 원점을 잇는 초록색 선분을 그린다.
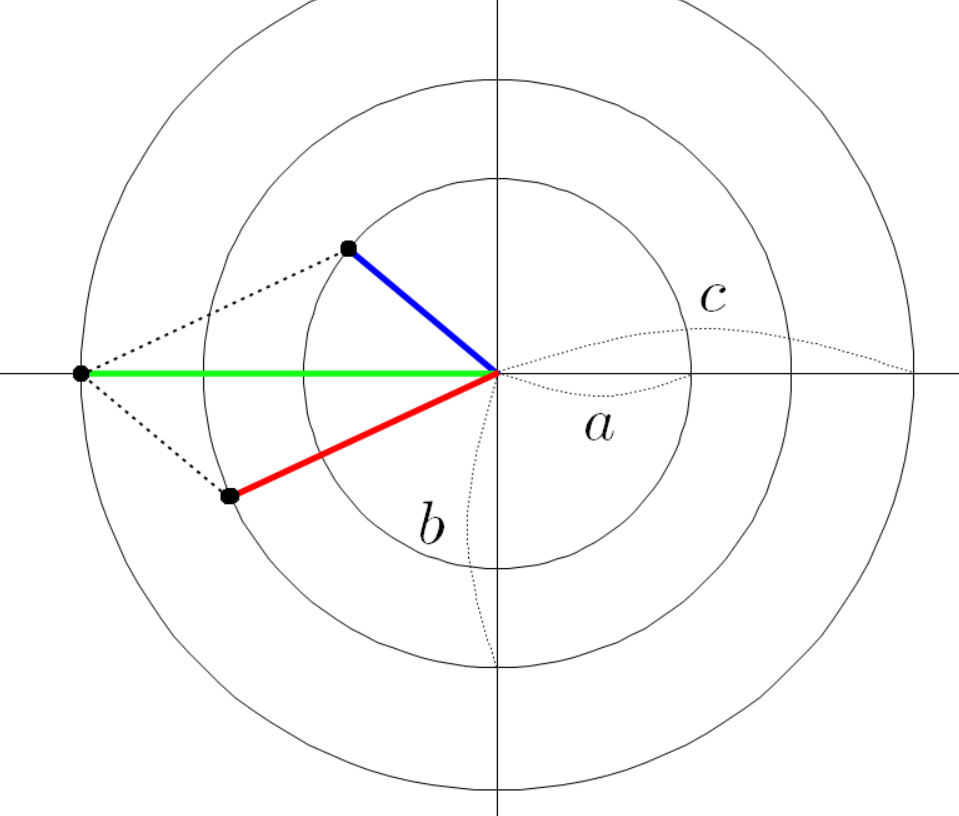

초록색 선분의 각도는 다음과 같다.
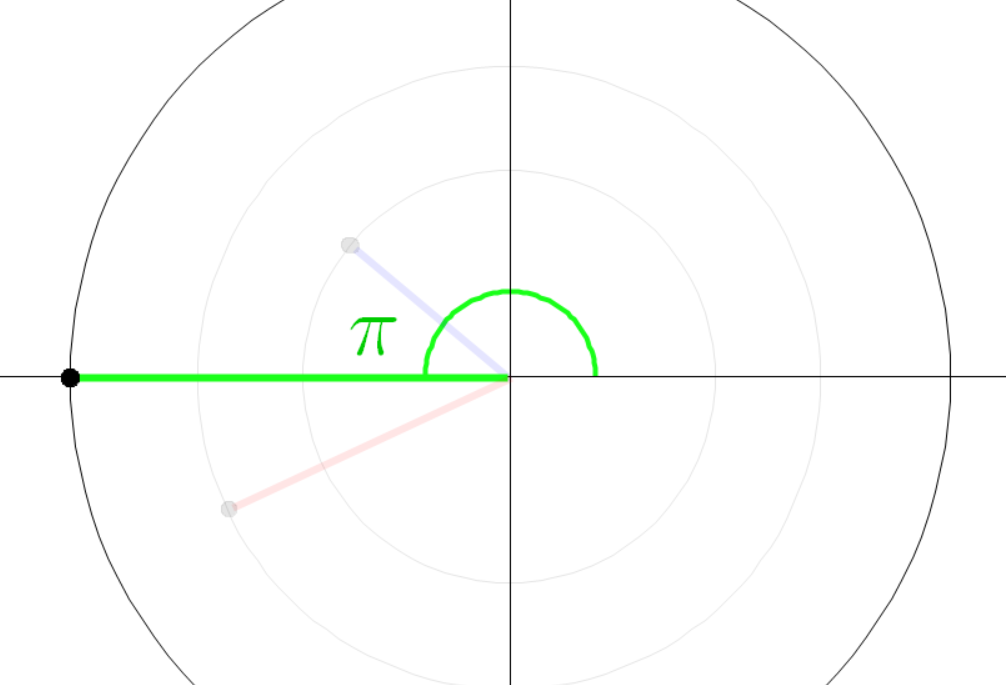
세 점의 좌표는 다음과 같다.
초록색 선분 끝 점의 좌표가 이렇게 계산되는 이유는
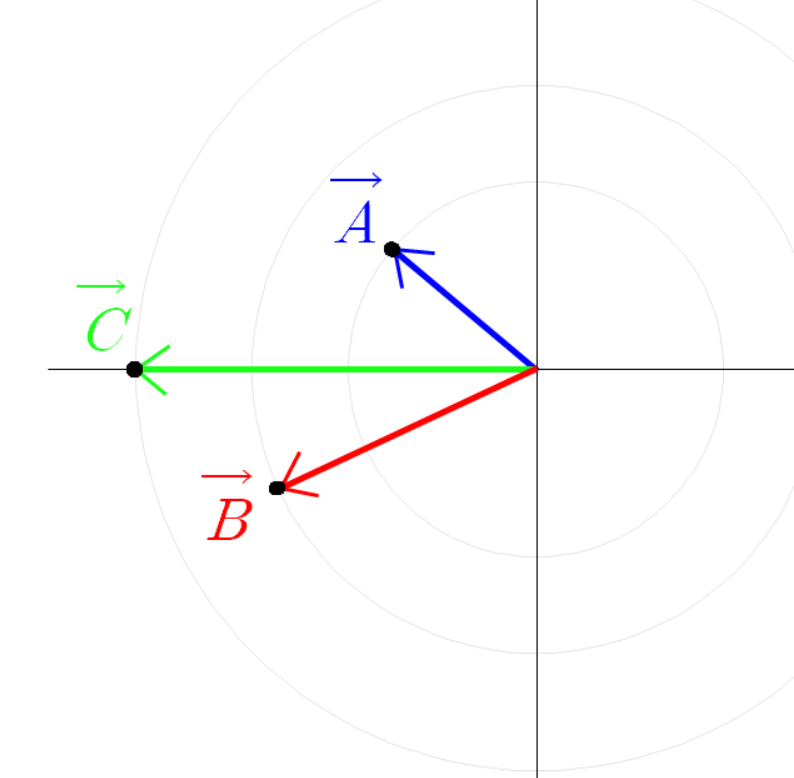
파란 선분 빨간 선분 초록 선분을 벡터로 본다면
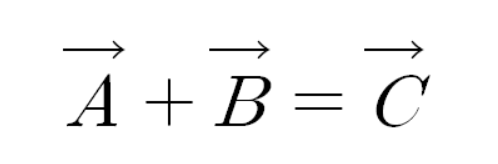
이(가) 성립하기 때문이다.
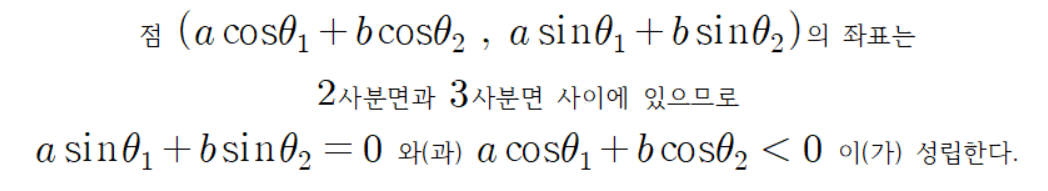
여기서

이때 초록색 선분의 높이는 다음과 같이 나타낼 수 있다.
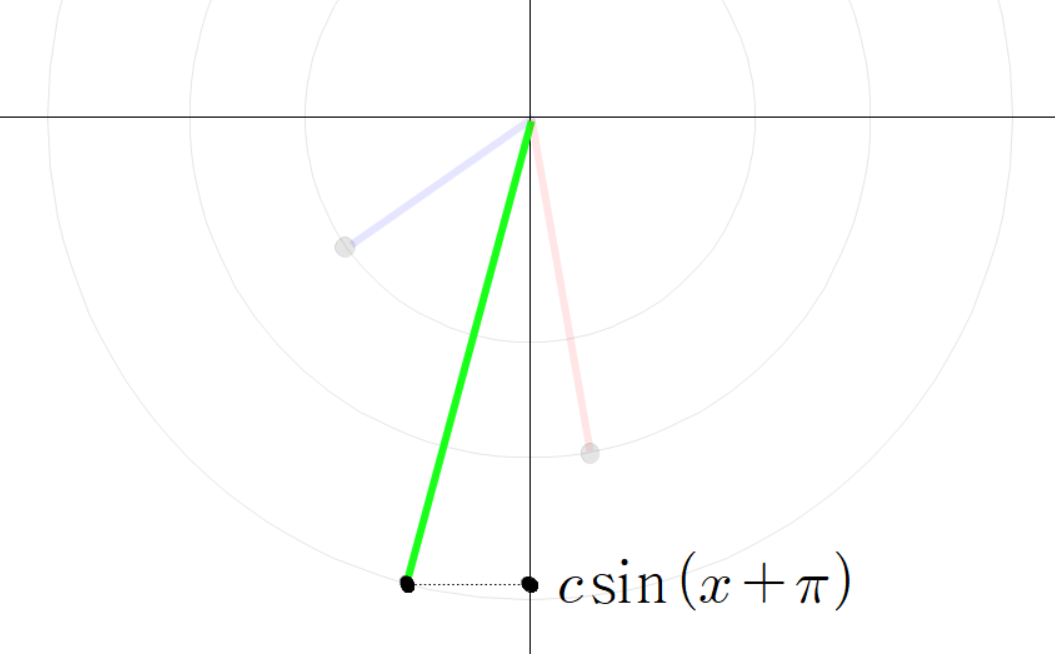
동시에 초록색 선분의 높이를 다음과 같이 계산할 수 있다.
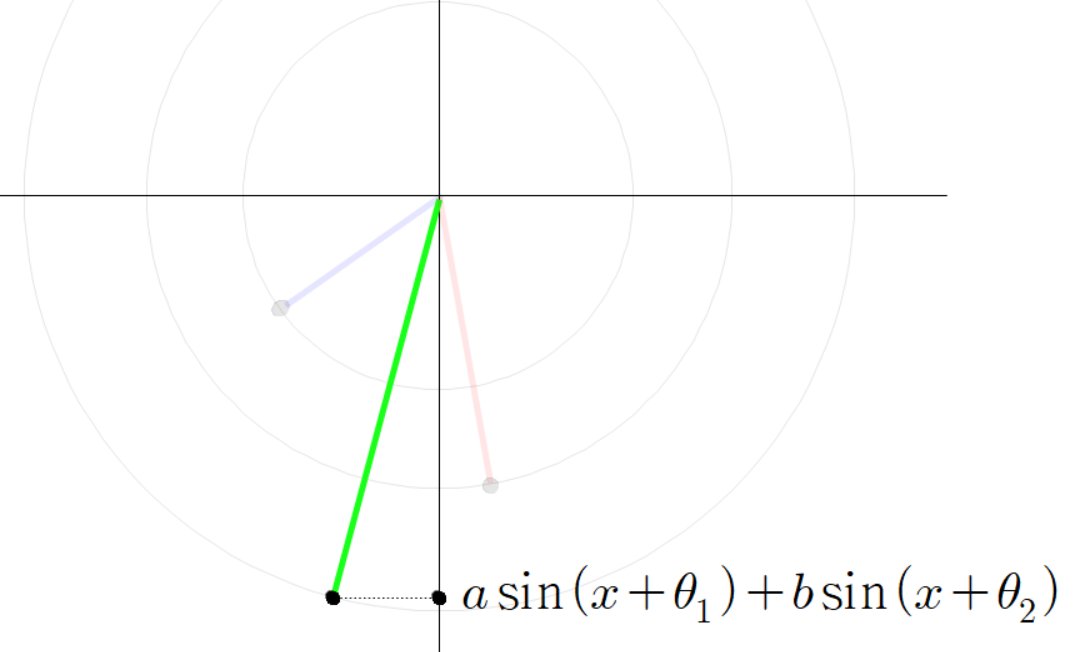
이유는 다음과 같다.
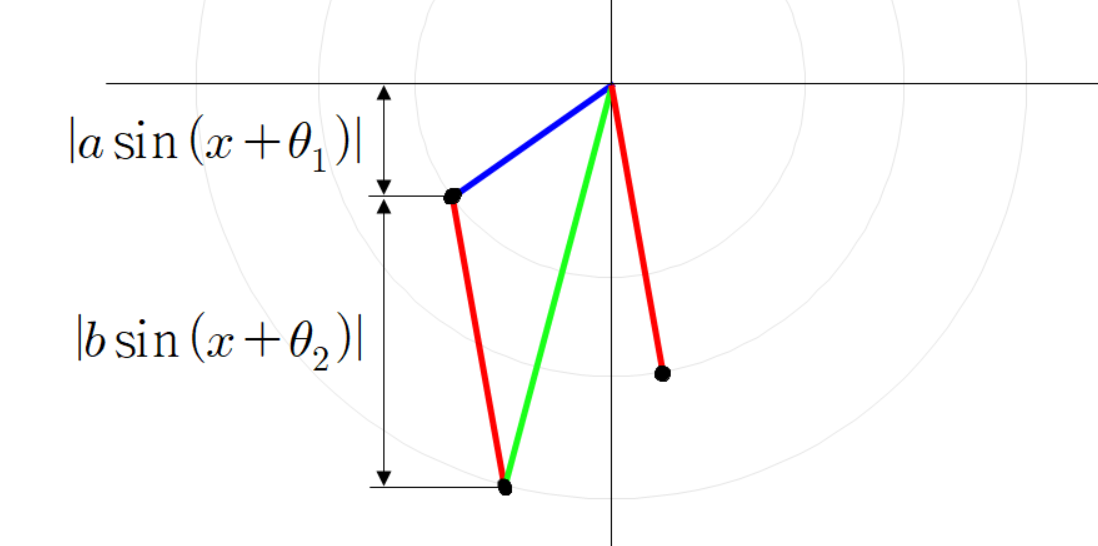
그러므로
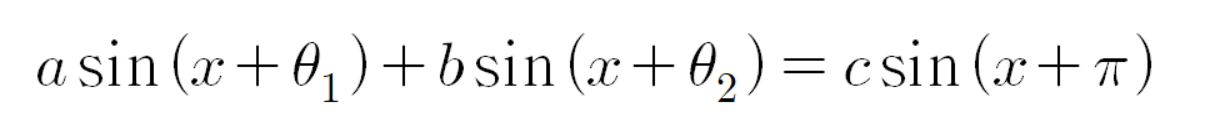
이다.
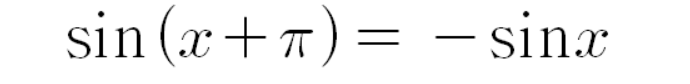
이므로
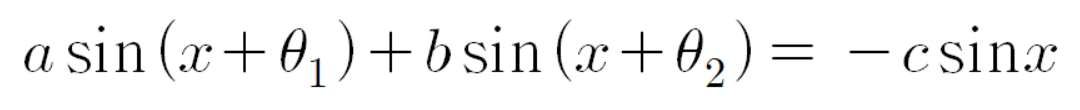
이다.

따라서 다음과 같은 결론이 나온다.

지금까지 나온 결론들을 모두 종합하여 보자.

이다.
그리고
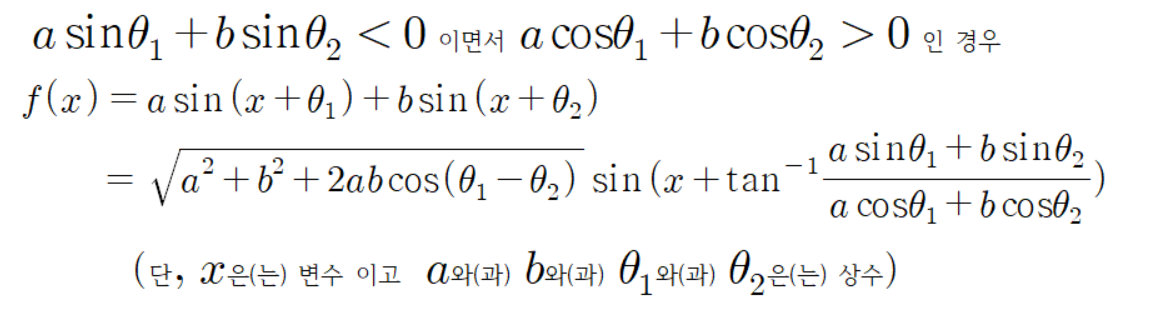
이다.

그리고
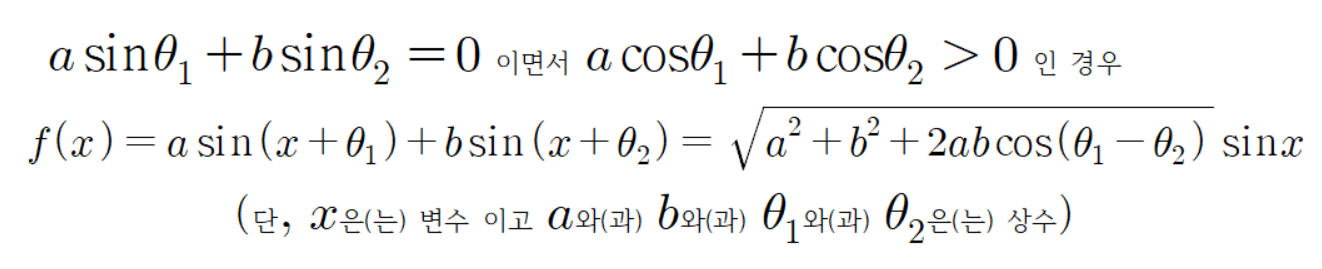
인데, 이는 다음과 같이 식을 유도할 수 있다.
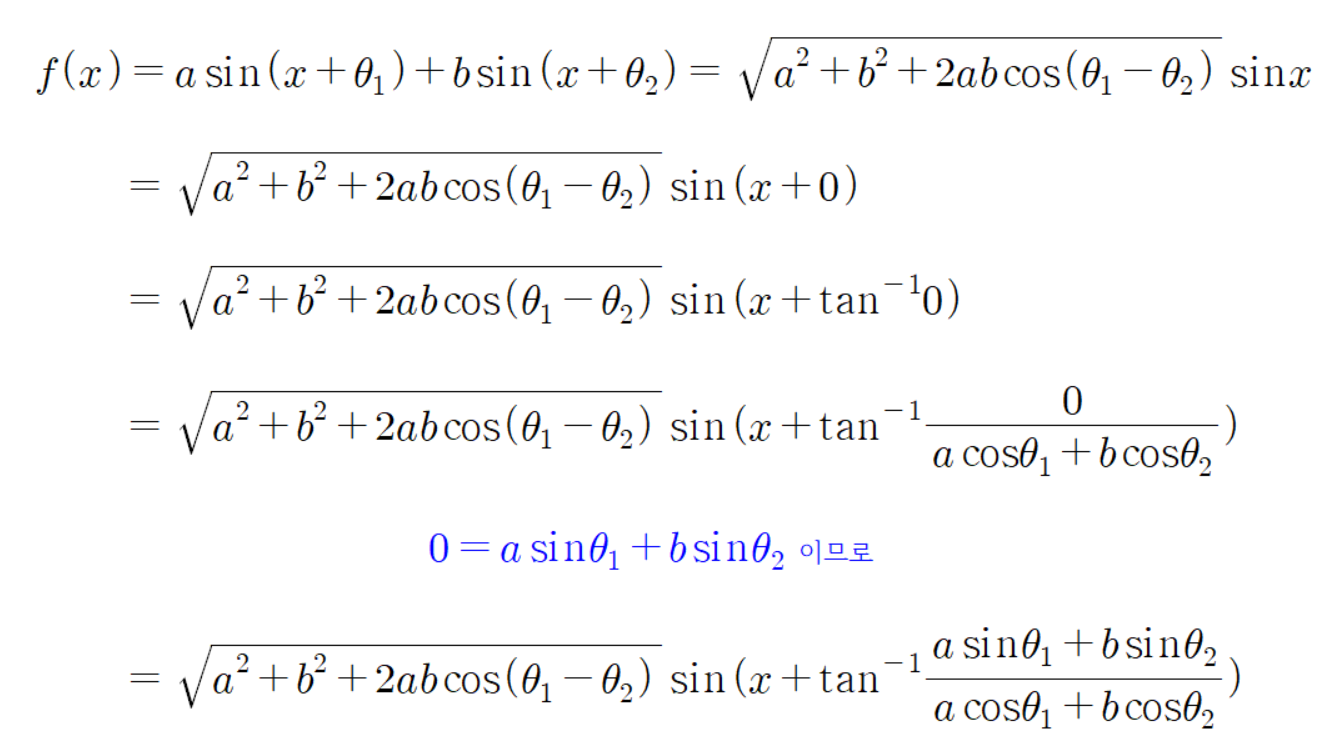
즉,
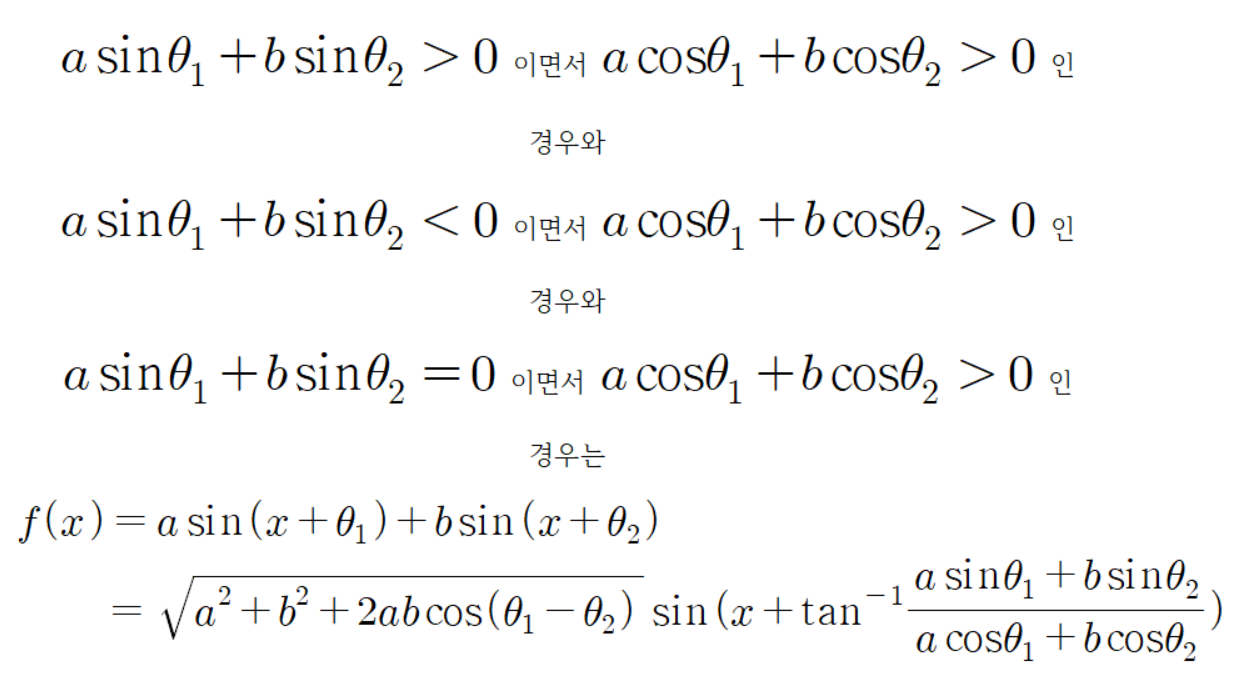
라는 결론으로 동일하다.
고로
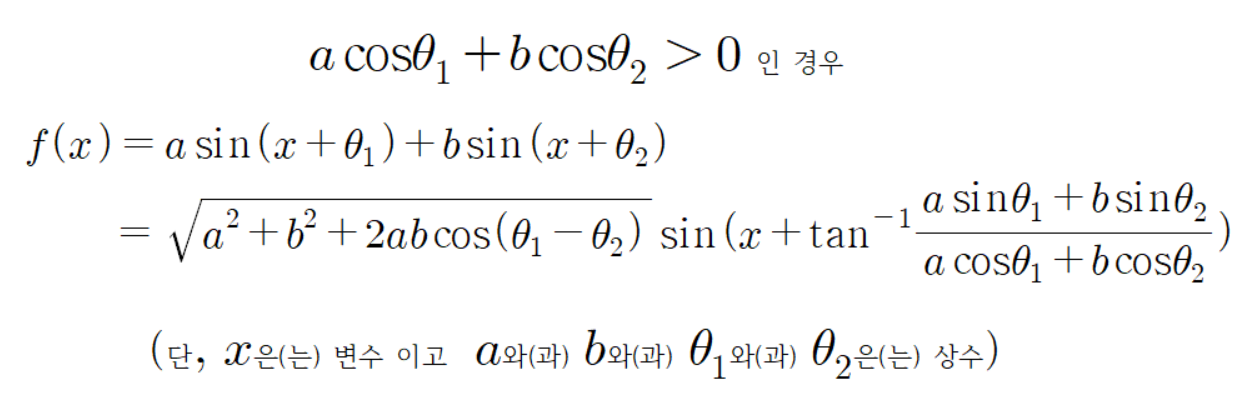
이다.
다른 경우들도 결론을 종합하여 보자.
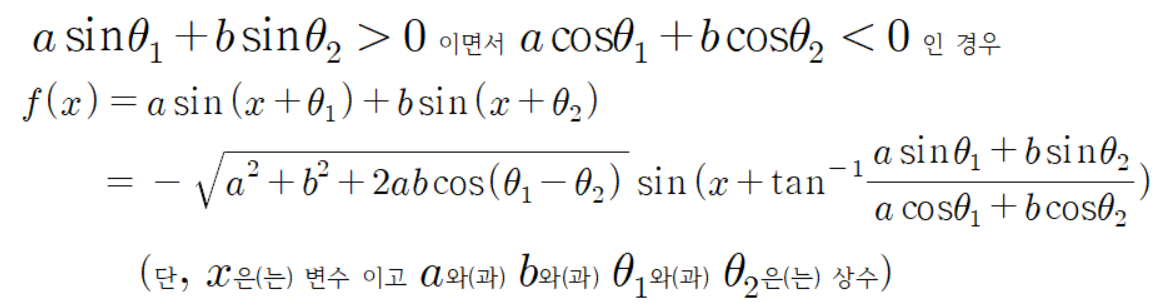
이다.
그리고
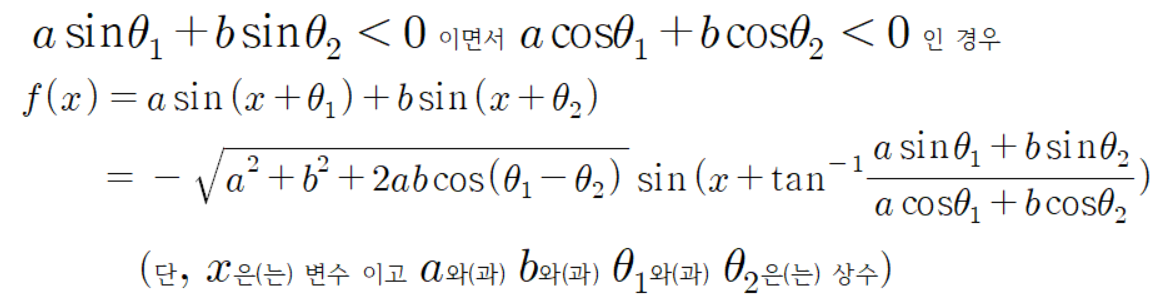
이다.

그리고
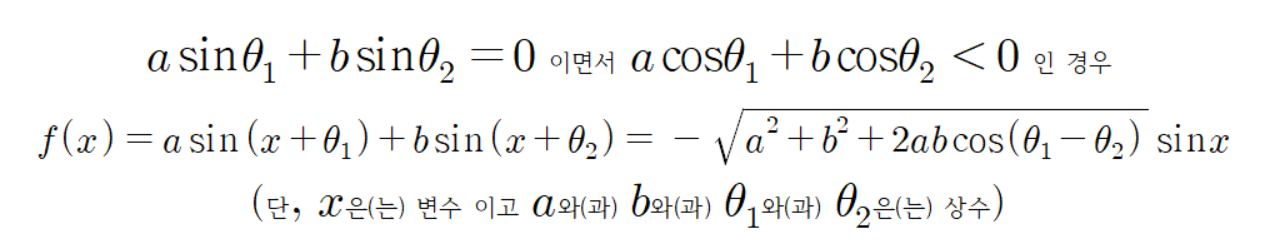
인데, 이는 다음과 같이 식을 유도할 수 있다.
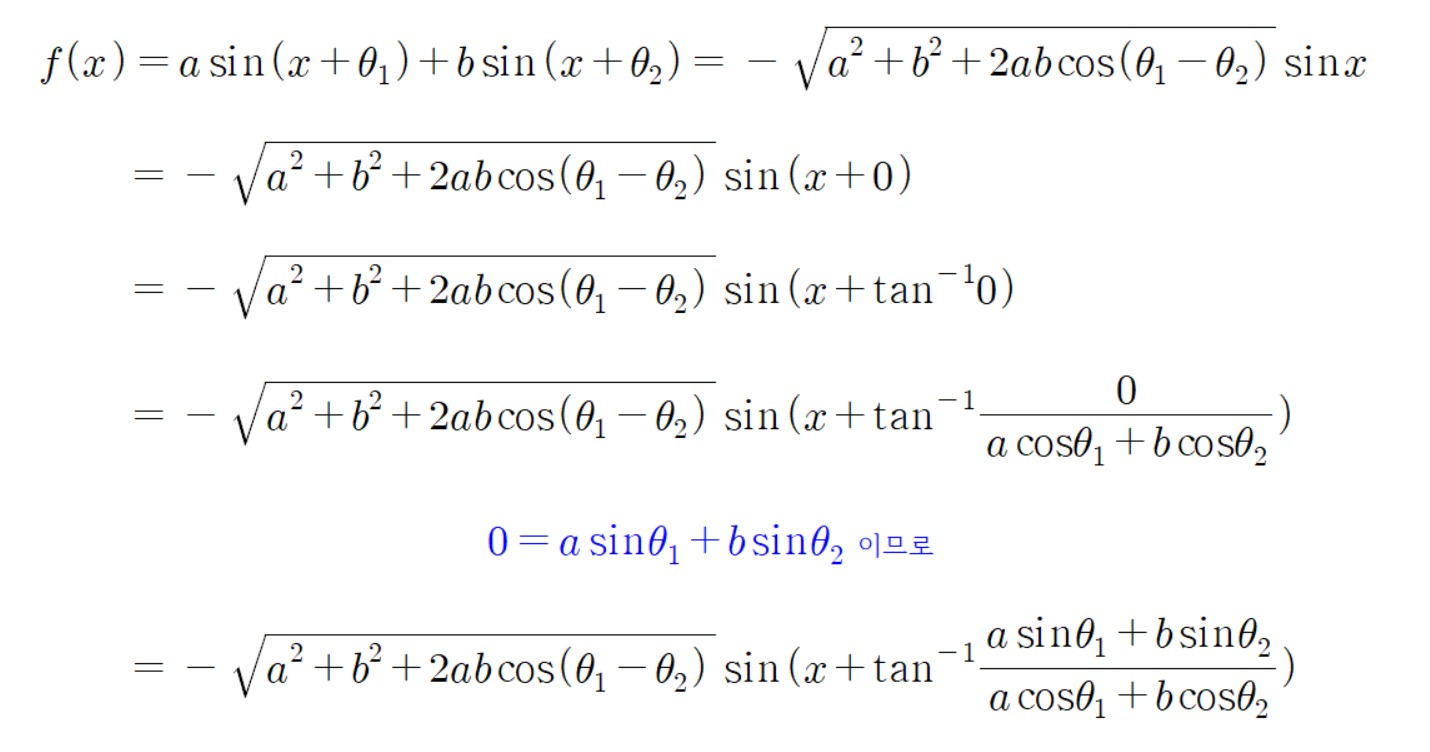
즉,
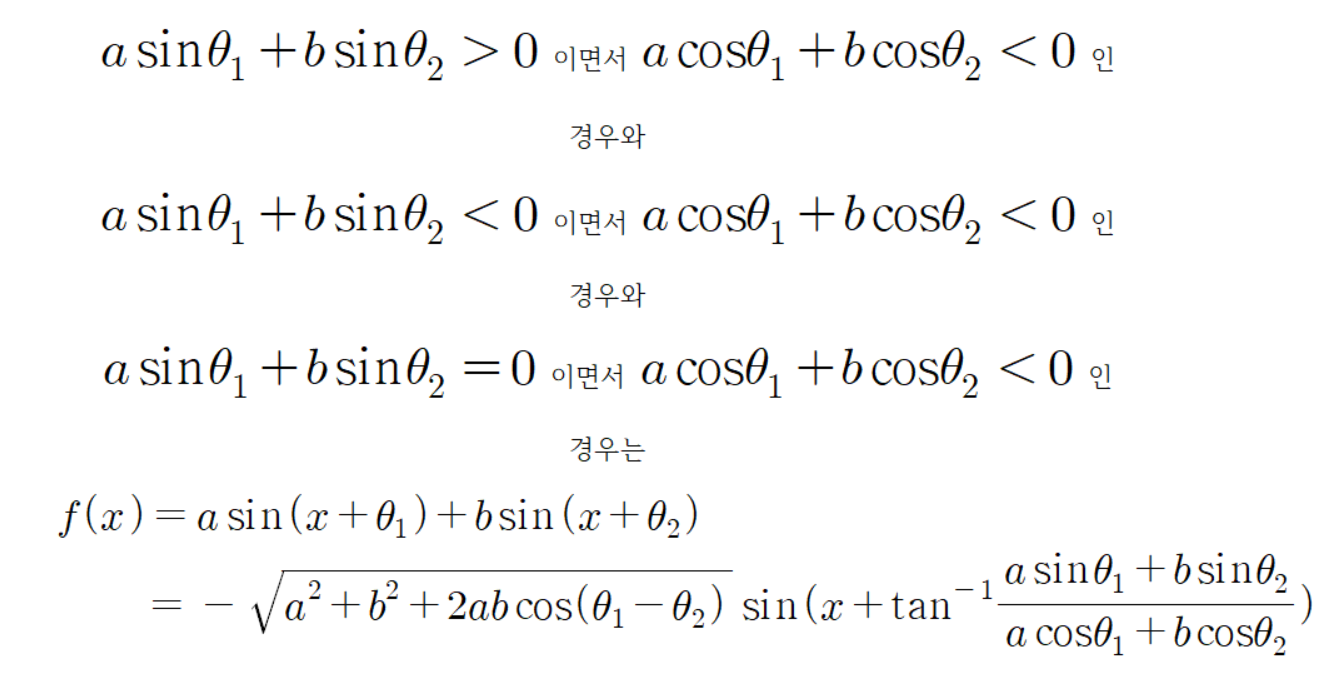
라는 결론으로 동일하다.
고로
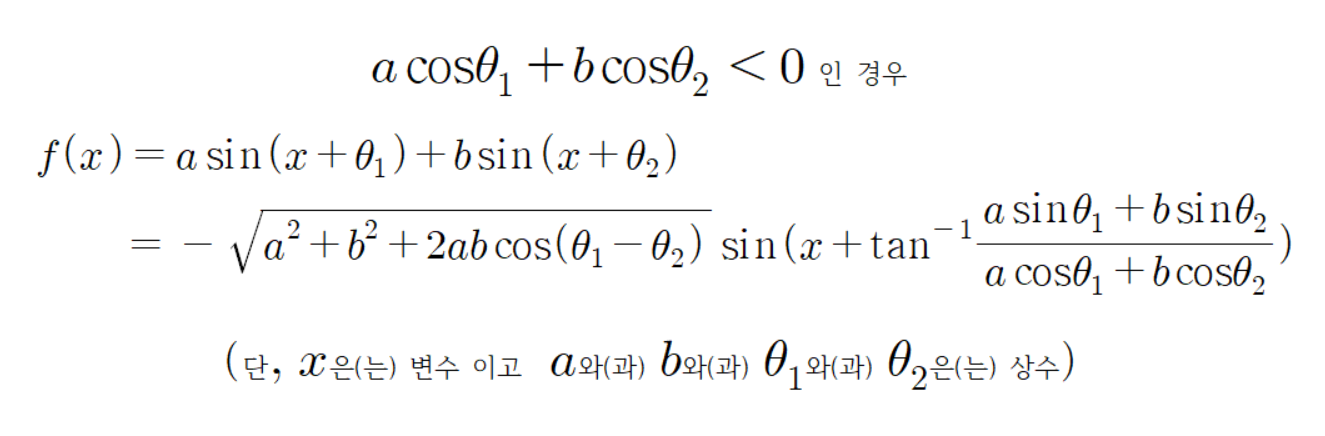
이다.
이제
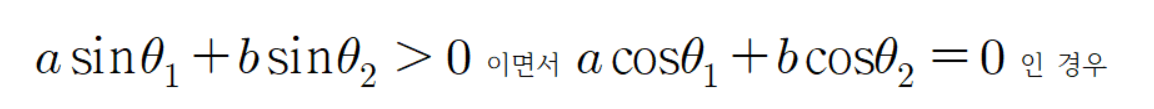
공식을 증명해 보자.
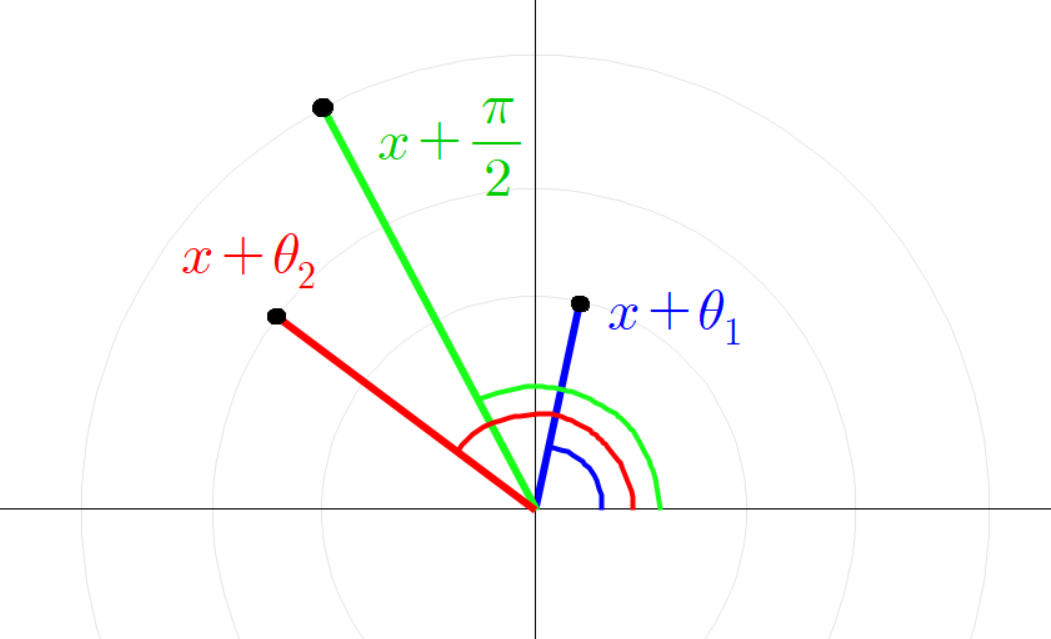
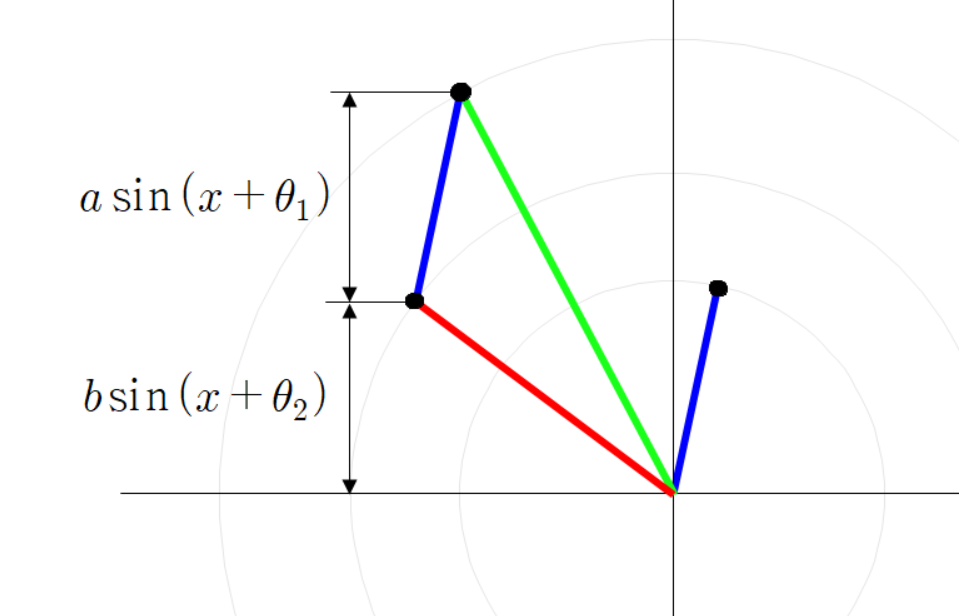
빨간 선분과 파란 선분의 각도가 다음과 같이 있다고 하자.
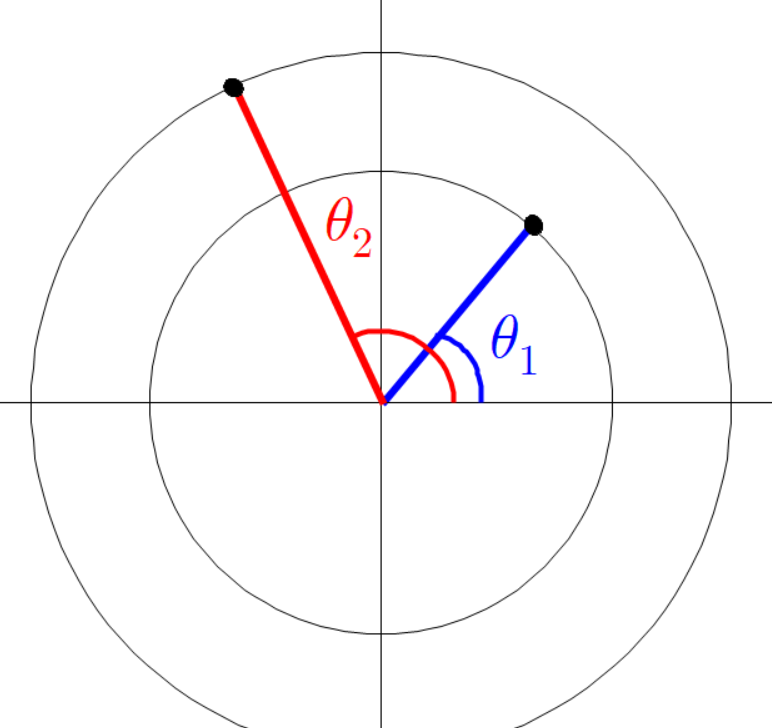
아까와 같이 평행한 두 점선을 긋고 그 점선의 교차점과 원점을 잇는 초록색 선분을 그린다.

초록색 선분의 각도는 다음과 같다.
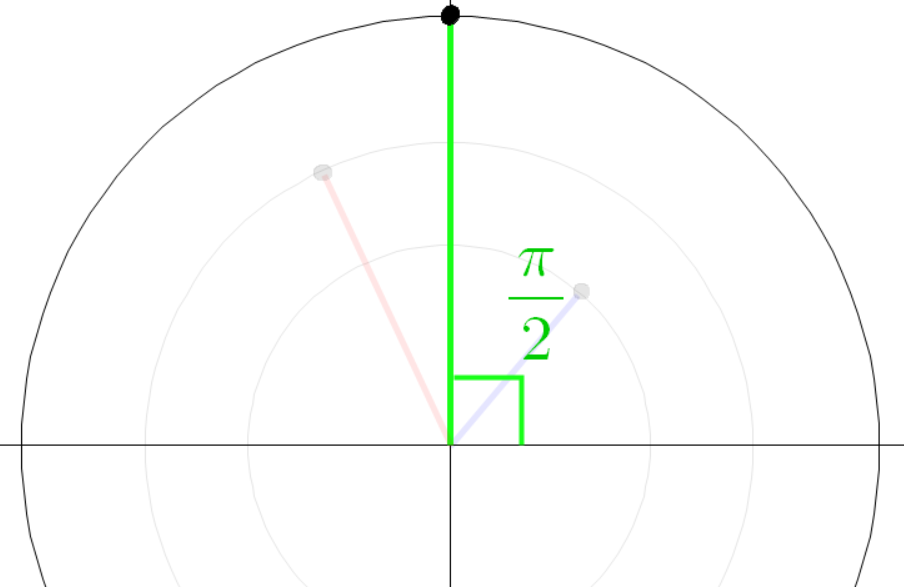
세 점의 좌표는 다음과 같다.
초록색 선분 끝 점의 좌표가 이렇게 계산되는 이유는
파란 선분 빨간 선분 초록 선분을 벡터로 본다면
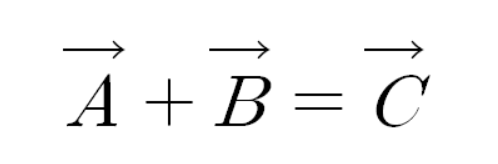
이(가) 성립하기 때문이다.

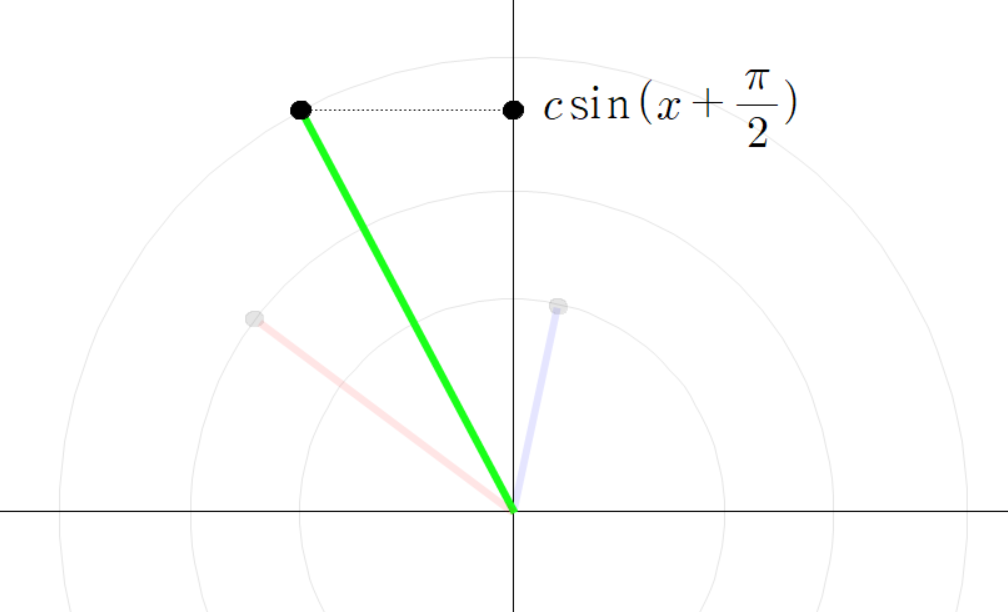
여기서

이때 초록색 선분의 높이는 다음과 같이 나타낼 수 있다.
동시에 초록색 선분의 높이를 다음과 같이 계산할 수 있다.
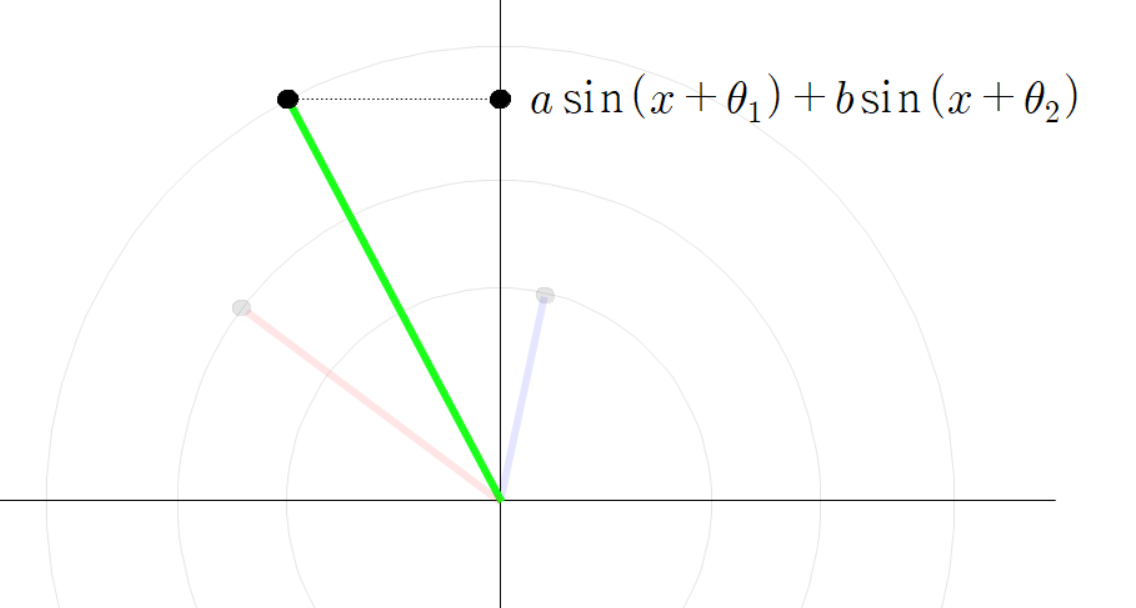
이유는 다음과 같다.
그러므로
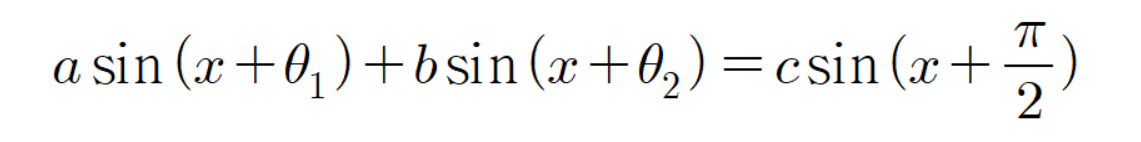
이다.

따라서 다음과 같은 결론이 나온다.
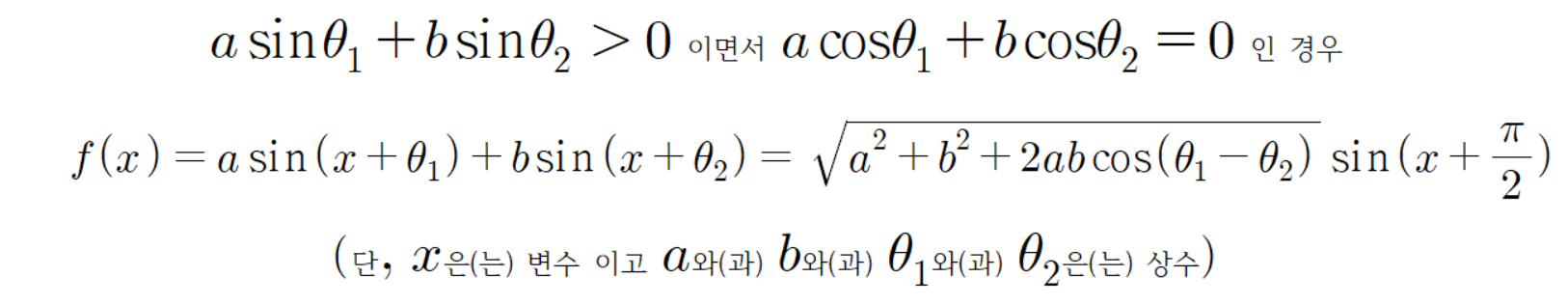
이제
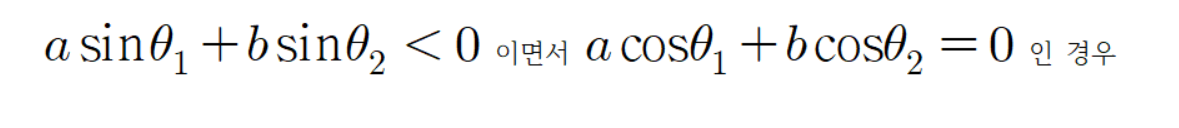
공식을 증명해 보자.
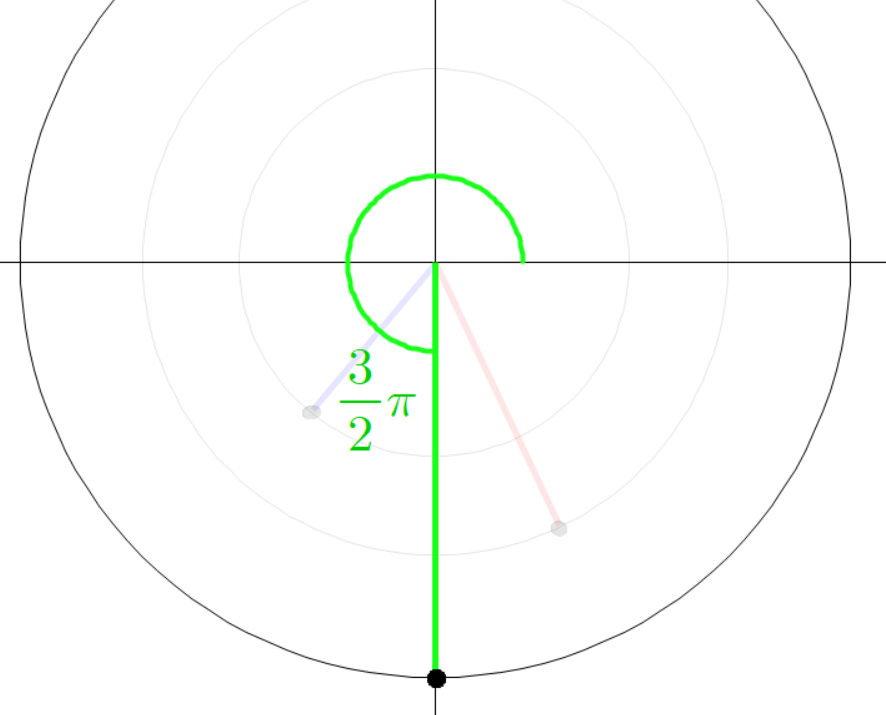
빨간 선분과 파란 선분의 각도가 다음과 같이 있다고 하자.
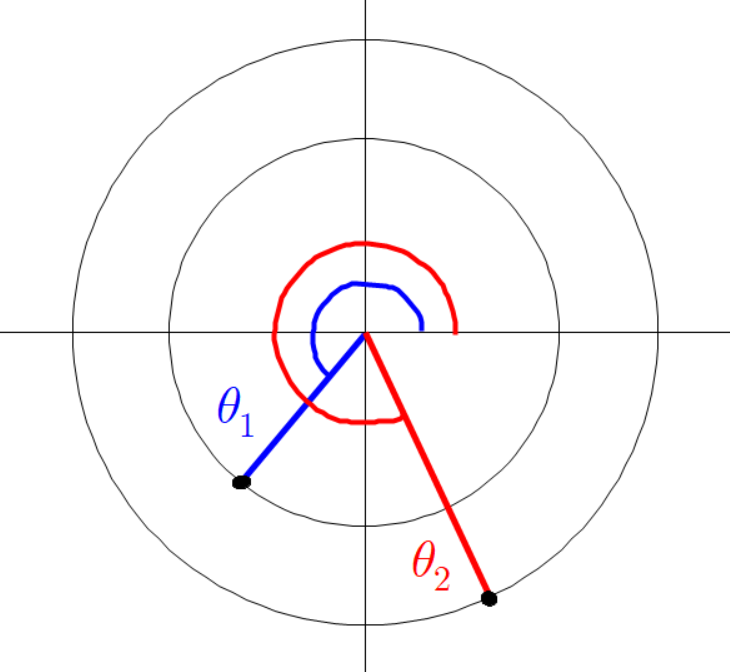
아까와 같이 평행한 두 점선을 긋고 그 점선의 교차점과 원점을 잇는 초록색 선분을 그린다.

초록색 선분의 각도는 다음과 같다.
세 점의 좌표는 다음과 같다.
초록색 선분 끝 점의 좌표가 이렇게 계산되는 이유는
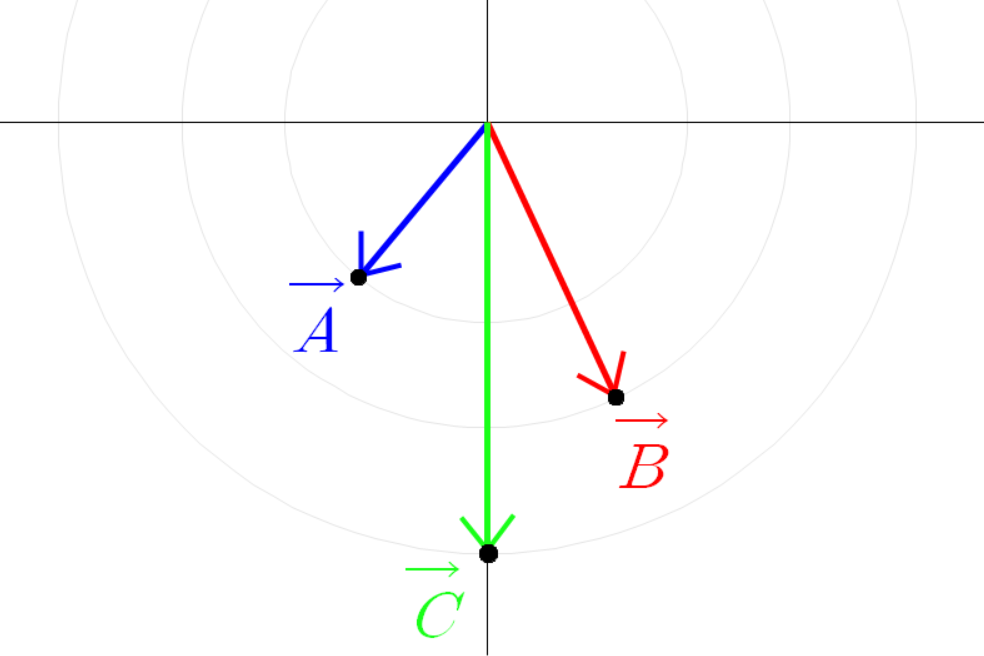
파란 선분 빨간 선분 초록 선분을 벡터로 본다면
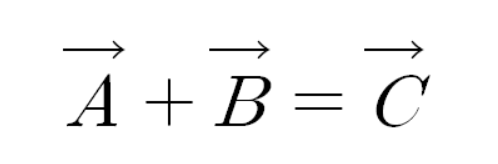
이(가) 성립하기 때문이다.

여기서

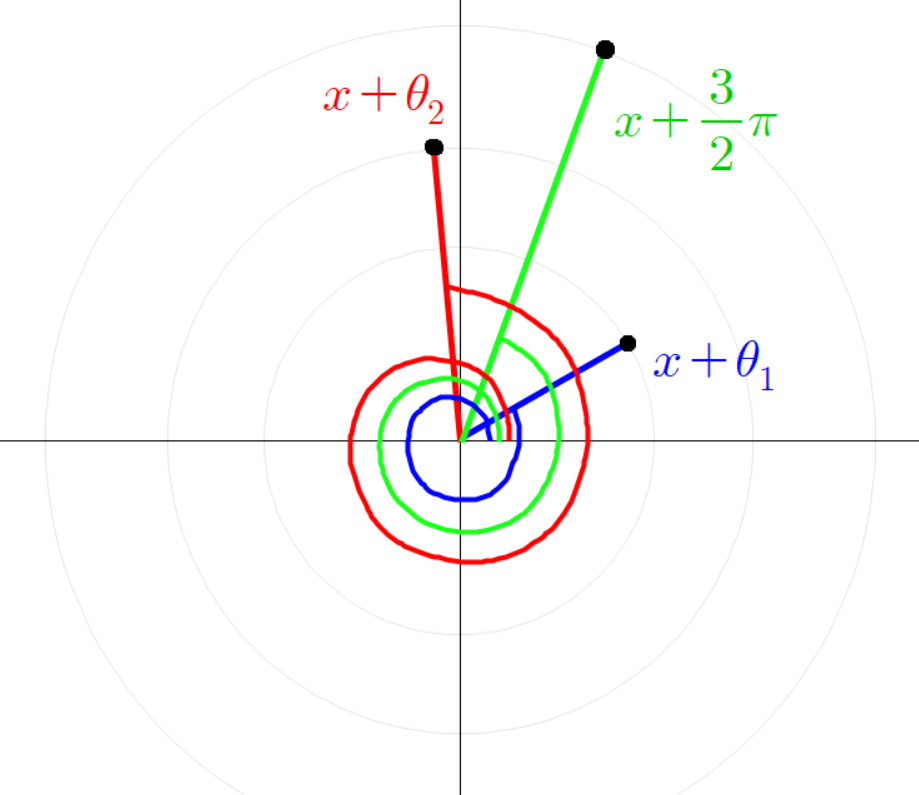
이때 초록색 선분의 높이는 다음과 같이 나타낼 수 있다.
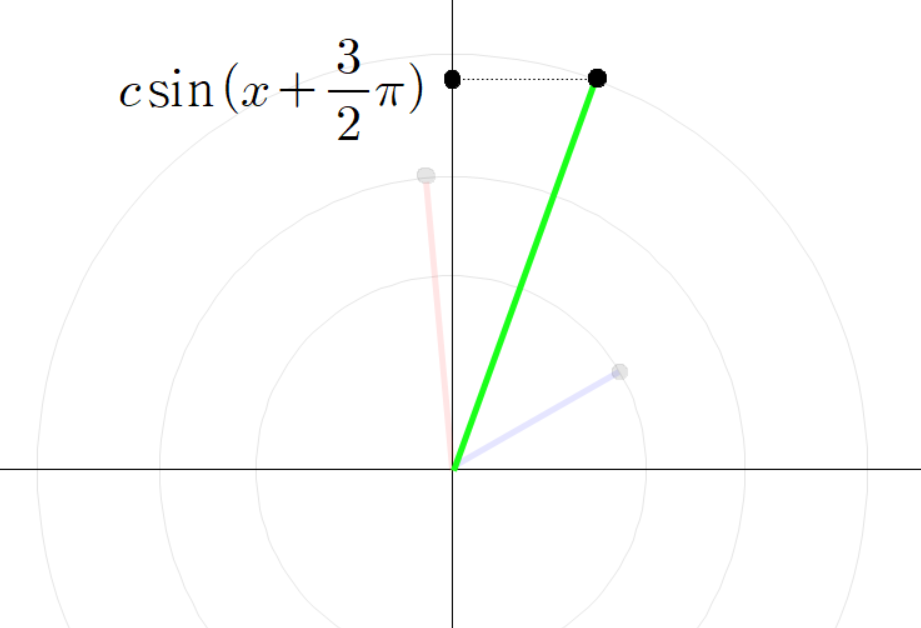
동시에 초록색 선분의 높이를 다음과 같이 계산할 수 있다.
이유는 다음과 같다.
그러므로
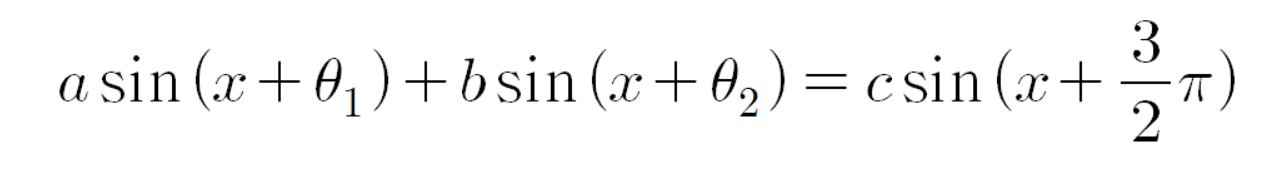
이다.

이므로
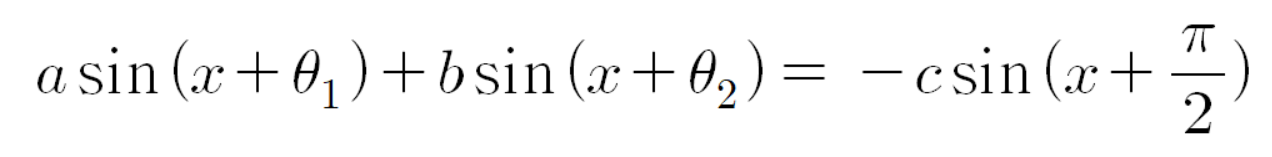
이다.

따라서 다음과 같은 결론이 나온다.
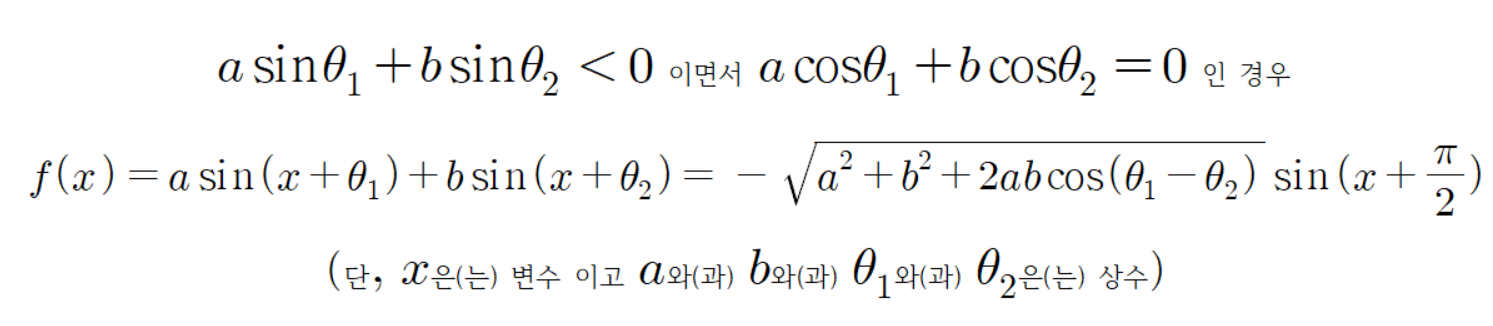
이제
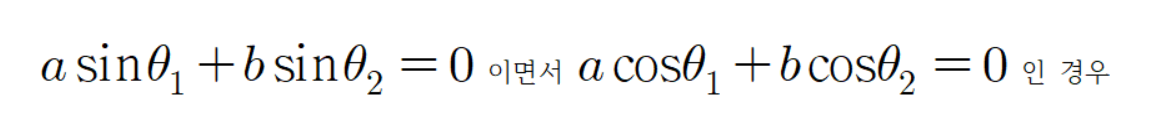
공식을 증명해 보자.

그러므로
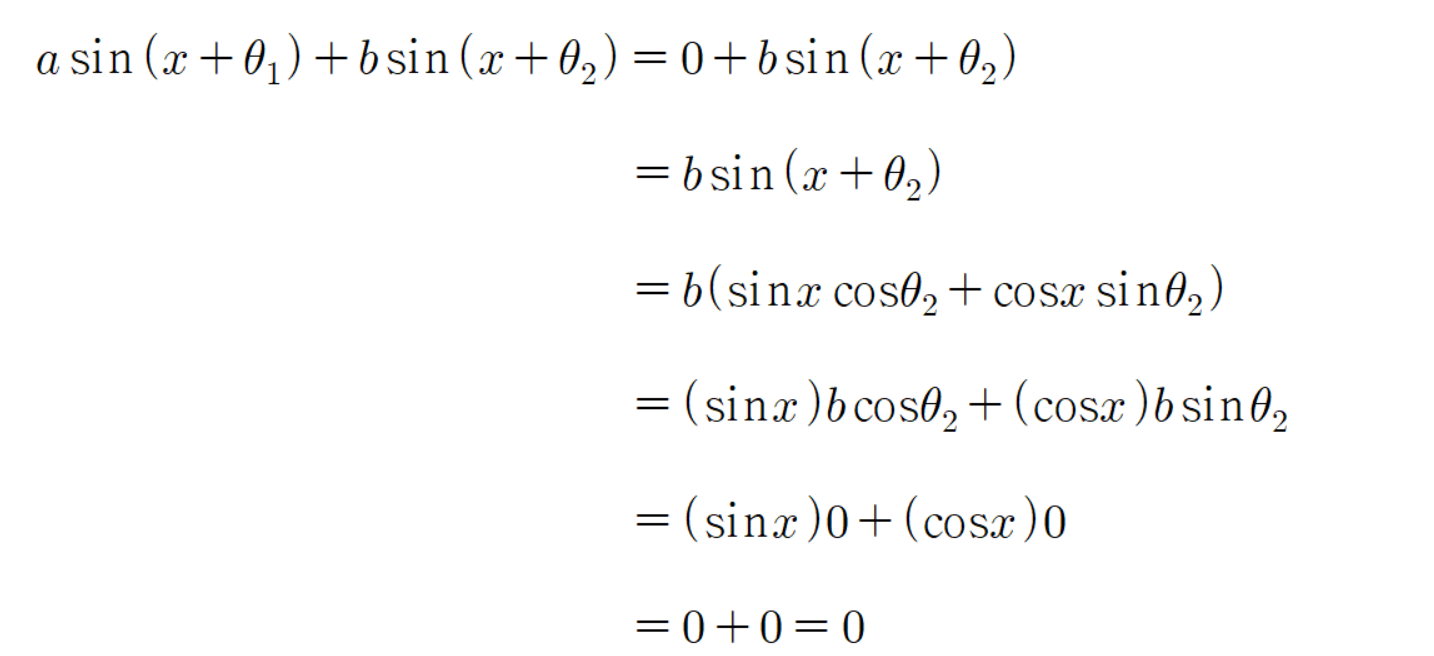
이다.

그러므로
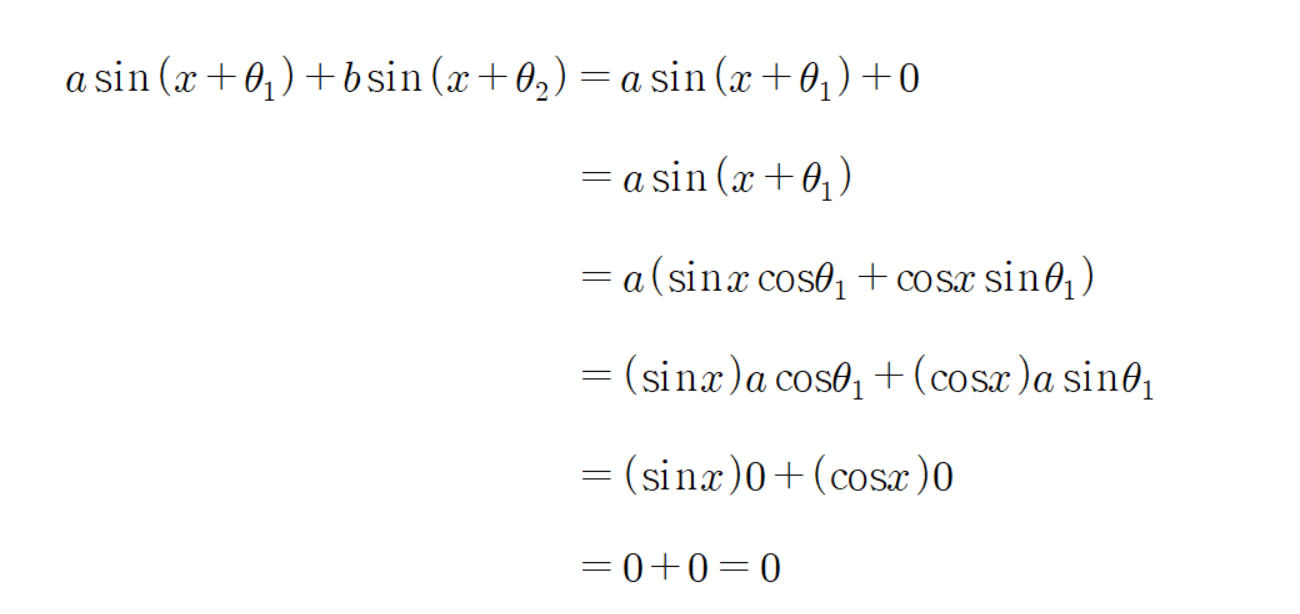
이다.

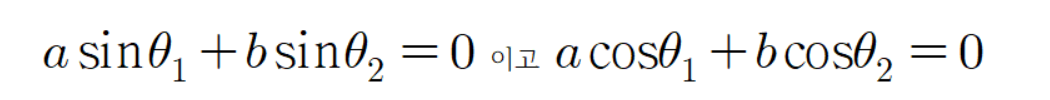
이므로 다음과 같은 계산을 할 수 있다.
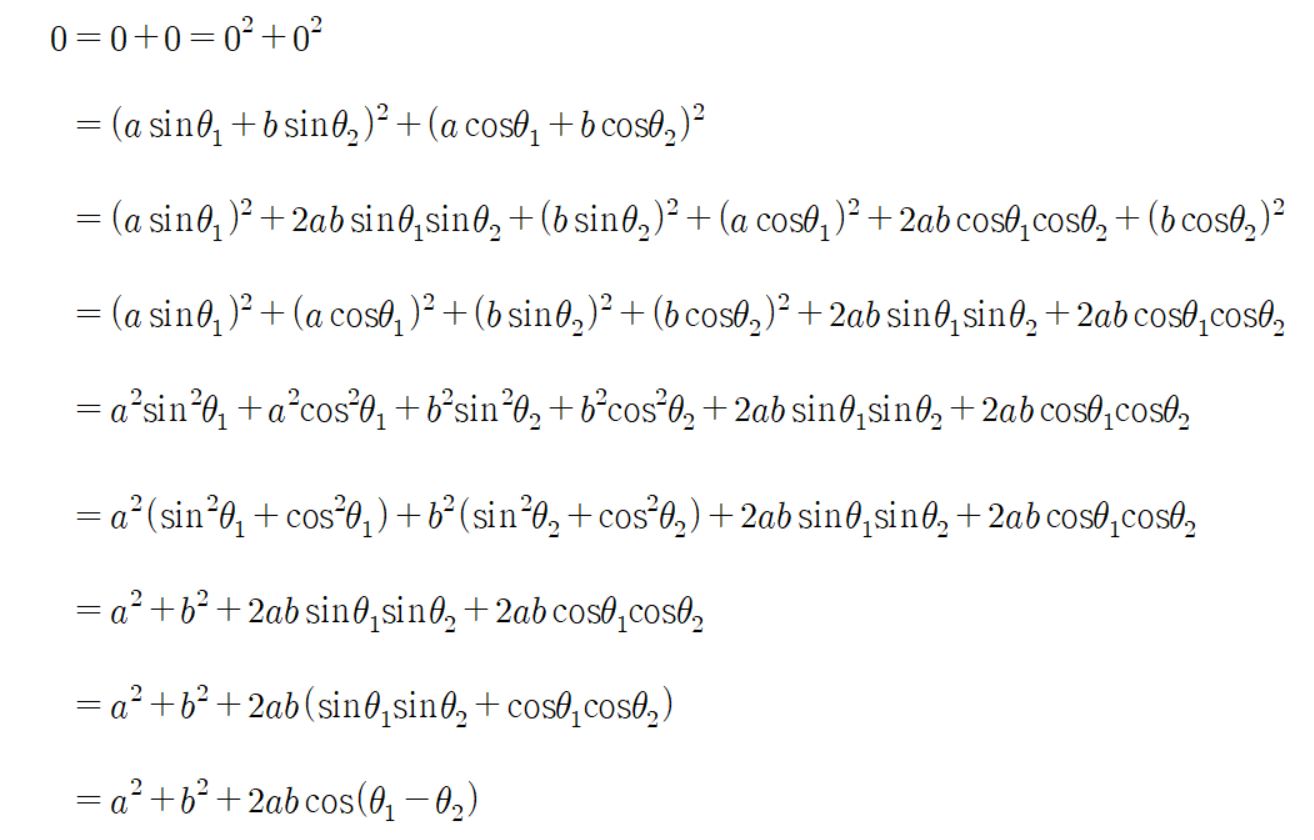
그러므로 다음과 같이 식을 유도할 수 있다.
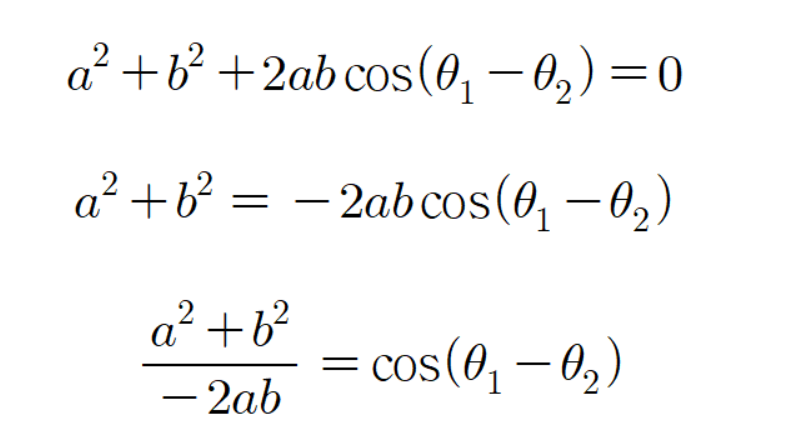
여기서
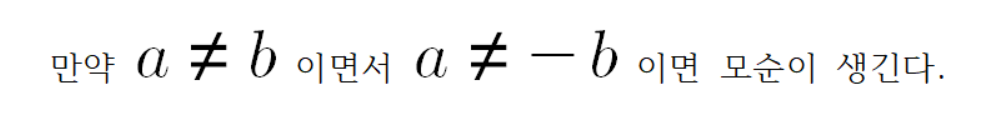
이유는 다음과 같다.
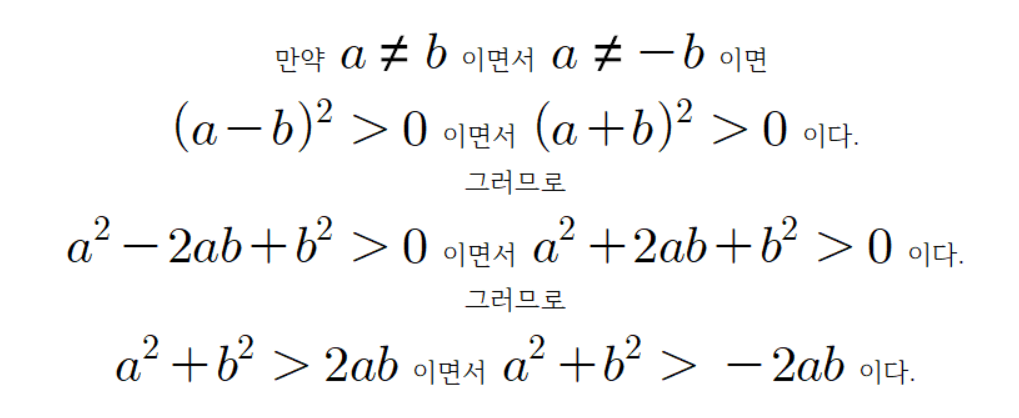
여기서
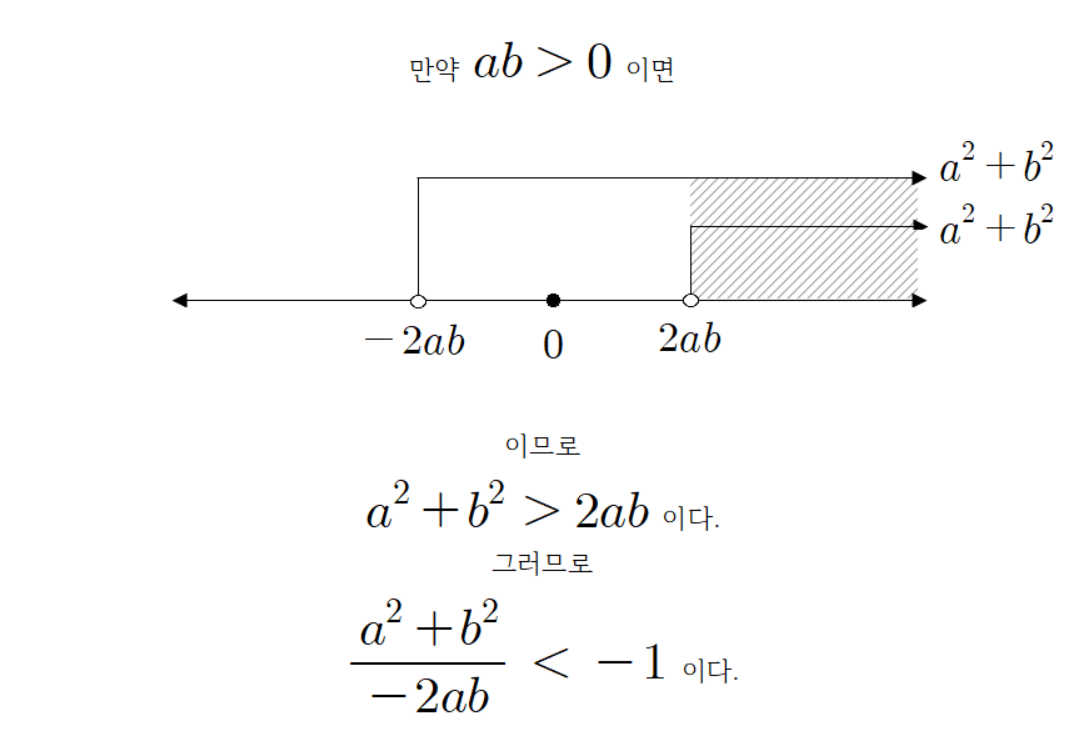
그리고
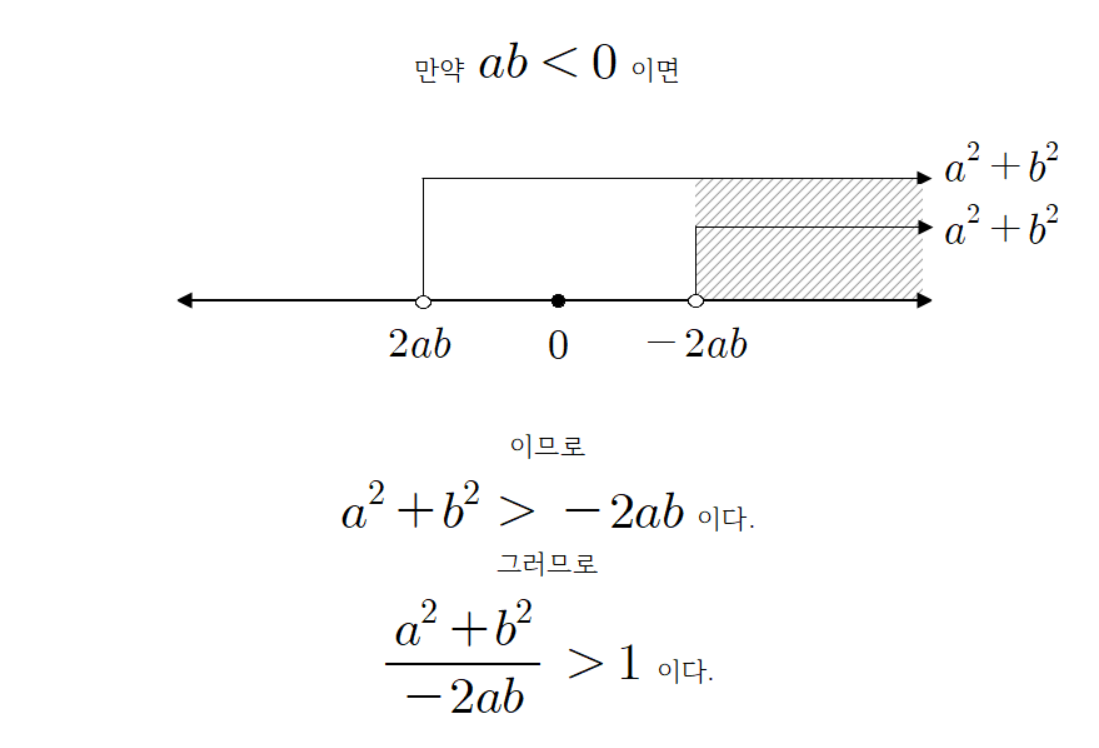
따라서

하지만

이것이 우리가 찾고자 했던 모순이다.
이는 모순 이므로 귀류법에 의해
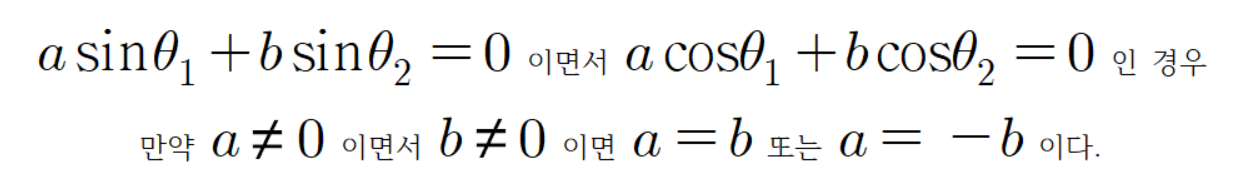
이 사실을 통해 다음과 같이 사실을 유도할 수 있다.
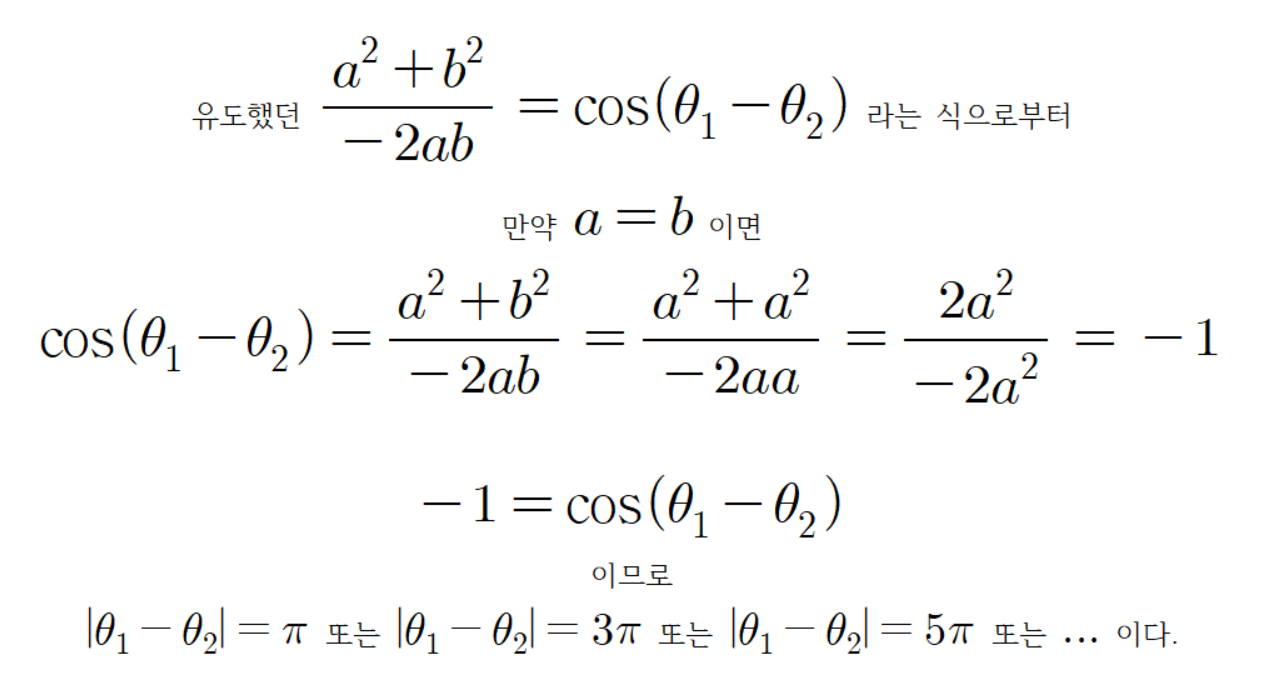
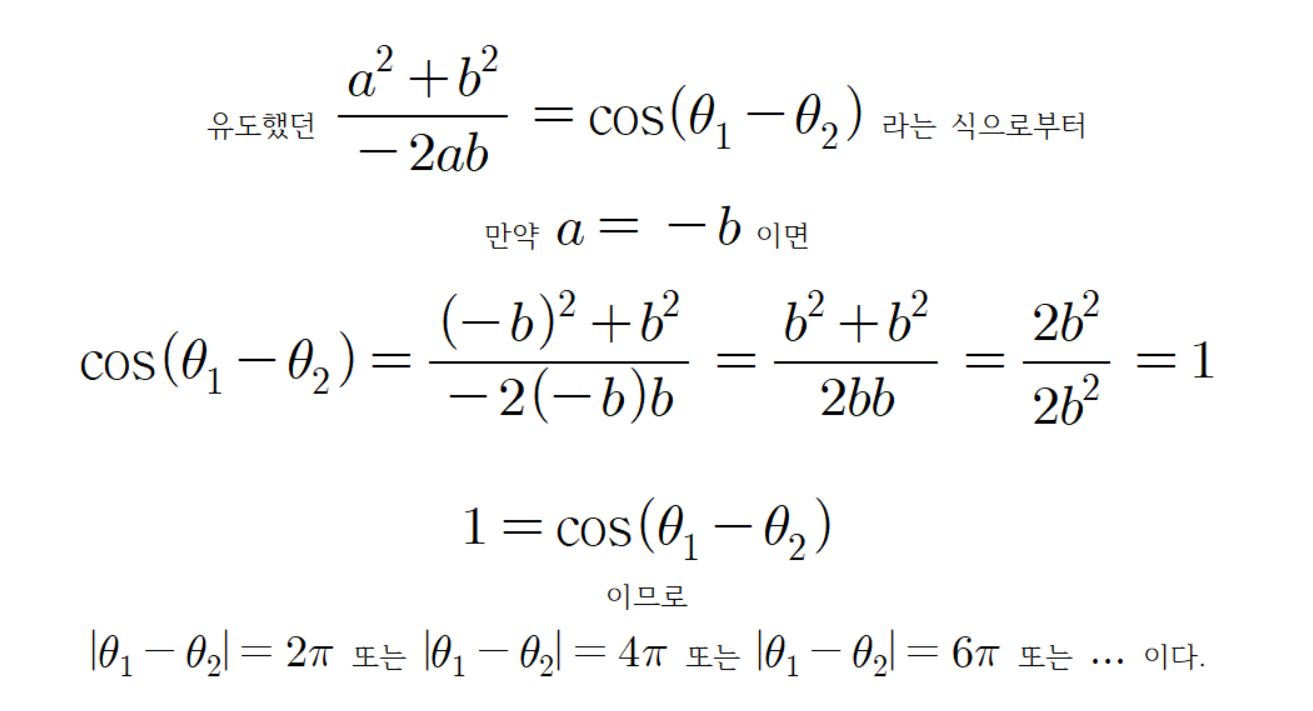
고로
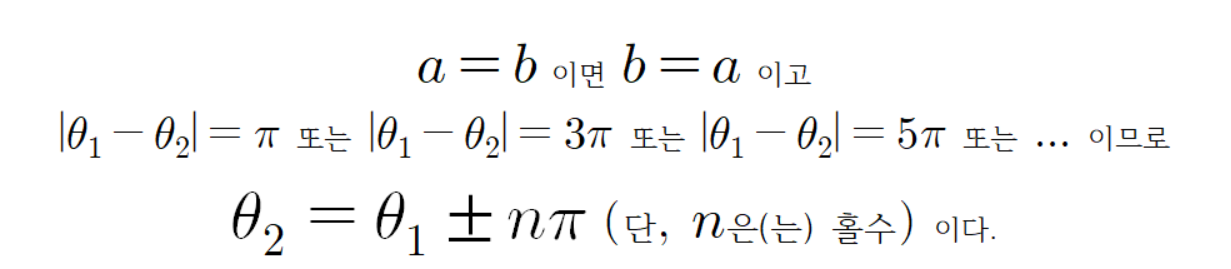
그리고

따라서

이고
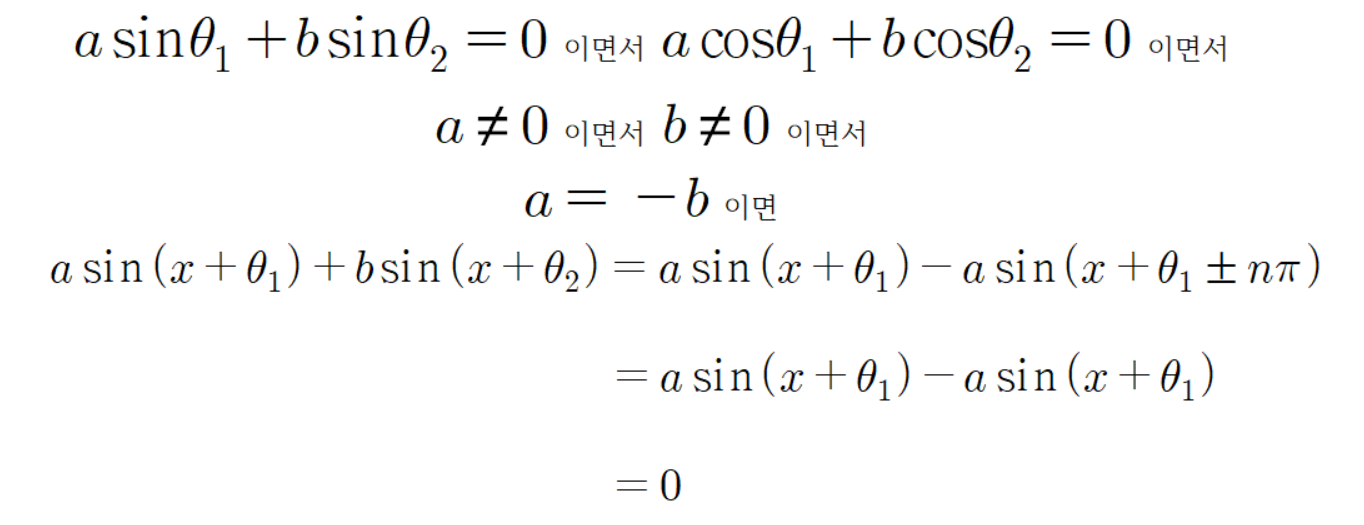
이다.
조금 전에 알아낸
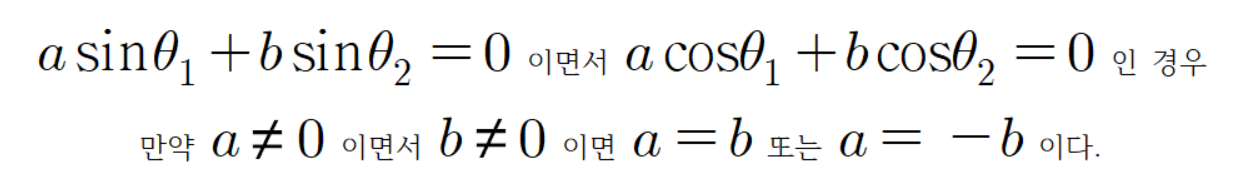
라는 사실을 통해 다음과 같은 결론을 낼 수 있다.
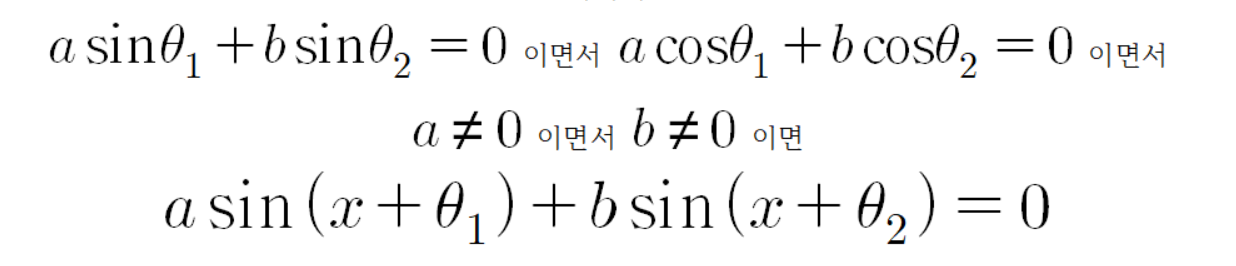
이다.
지금 까지 나온 결론들을 표로 정리하여 종합하여보자.

따라서
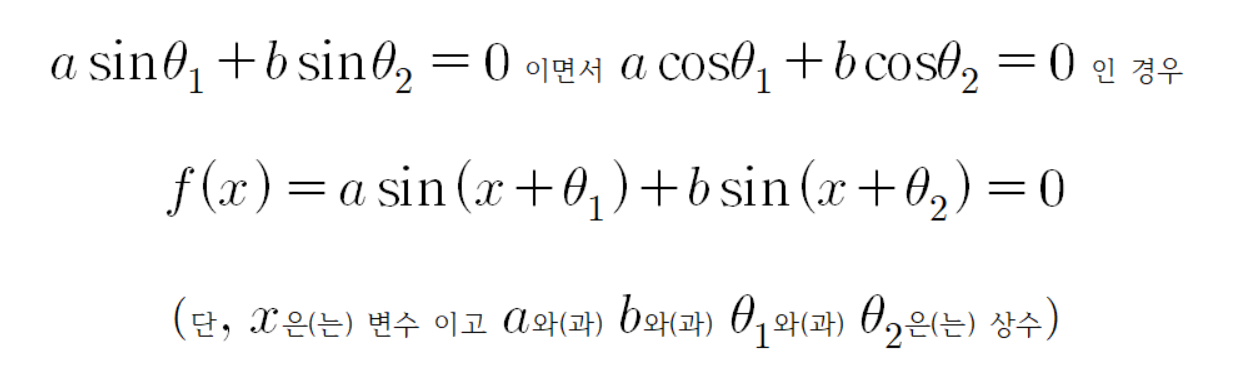
이다.
지금까지 나온 모든 결론들을 표로 정리하여 보자.

이 공식은 모든 실수 x에서 항상 성립한다.
'수학' 카테고리의 다른 글
| 삼각함수 합성공식과 페이저 3편(삼각함수 벡터공간과 복소수 벡터공간의 동형사상) (0) | 2021.11.25 |
|---|---|
| 삼각함수 합성공식과 페이저 2편(삼각함수 집합과 복소수 집합은 벡터공간) (0) | 2021.11.23 |
| 오일러 공식 (0) | 2021.11.22 |
| 테일러 급수 (0) | 2021.11.21 |
| 로그함수 음수구간 (2) | 2021.10.25 |