2021. 11. 21. 00:51ㆍ수학
이번에는 테일러 급수라는 재미난 수학을 알아보자.
테일러 급수 또는 테일러 전개라고 불리는 것은
해석하기 어려운 함수를 다항함수 꼴로 바꾸는 과정을 말한다.
이번 주제의 수학은 고등 수학 범주에 없는
대학 수학이다.
하지만 고등학생 시절 미적분 공부를 열심히 한 분들께서는
어려움 없이 아주 쉽게 알아볼 수 있는 내용이니
필자와 같이 도전해보자.
이번 주제를 공부하기 앞서
미리 알고 있어야 하는 수학 개념들을 소개하겠다.
필자는 이번 포스팅에서 지수 함수와 삼각함수를 테일러 전개할 것이다.
그러므로 당연히 지수 함수와 삼각함수가 무엇인지 알아야 한다.
필자는 자연 상수 e를 밑으로 하는 지수 함수를 테일러 전개할 것이므로
당연히 자연 상수e에 대한 것도 알고 있어야 한다.
테일러 전개에는 미분 개념이 필수이다.
지수 함수 미분, 삼각함수 미분 이 두 가지는 꼭 공부하고 오기 바란다.
테일러 전개란 어려운 해석 함수를 다항함수 꼴로 바꾸는 과정이다.
다항함수의 미분도 공부하기 바란다.
다항함수가 급수 형태로 뻗어 나가므로
이를 표기하기 쉽게 하려면 시그마 기호가 필요하다.
시그마의 정의만 공부해 와도 충분하다.
마지막으로 팩토리얼 기호의 정의까지 알고 오기 바란다.
이제 시작해보자.
함수 f(x)를 다음과 같은 지수함수로 정의하겠다.

그런데 이 f(x)를 다음과 같은 다항함수 꼴로 바꿀 수 있을까?

만약 바꿀 수 있다면 다음과 같은 관계식을 세울 수 있다.

여기서 우리는 양 변을 계속 미분해 나가며 0을 대입할 것이다.

이번에는 양변을 미분하겠다.

이번에는 양변을 한번 더 미분하겠다.
그럼 다음과 같이 나온다.

이번에는 양변을 또 한번 더 미분하겠다.

이렇게 정의한 값들을 처음식에다 대입하면
다음과 같은 결론을 낼 수 있다.
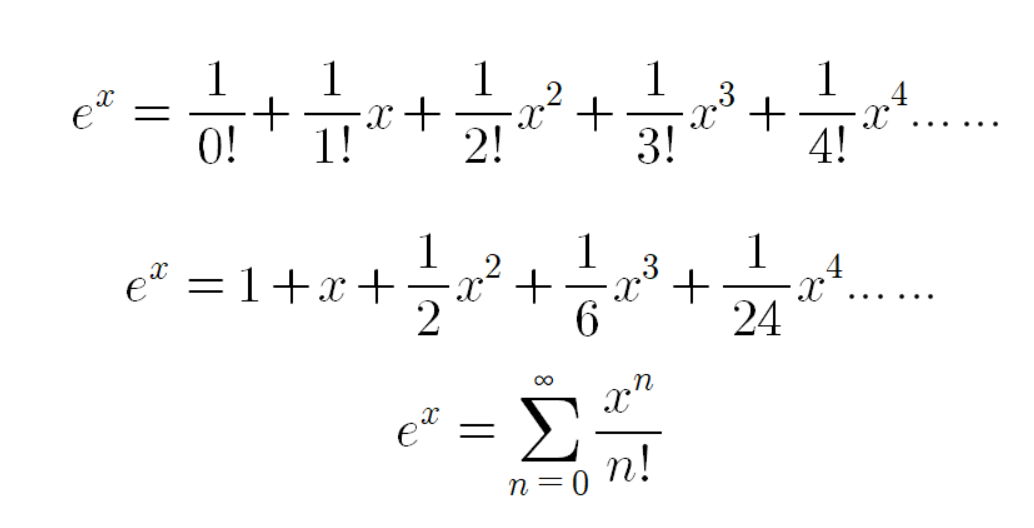
이것이 지수함수를 테일러 전개한 결과이다.
우리는 지수함수를 테일러 전개하였다.
이제 싸인 함수와 코싸인 함수를 테일러 전개 해보자.
지수함수의 테일러 전개 했던 방식을 똑같이 적용하면 된다.
했던 방식 그대로 다음과 같이 식을 세운다.
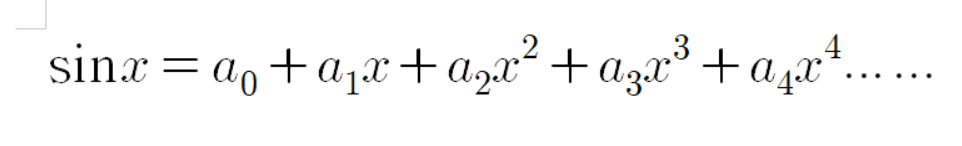
여기서 양변을 미분하고 0대입하기를 반복하여 다항함수의 개수들을 정의해 나가면 된다.
그럼 싸인을 미분해 나가면 어떤 어떤 모습일까?
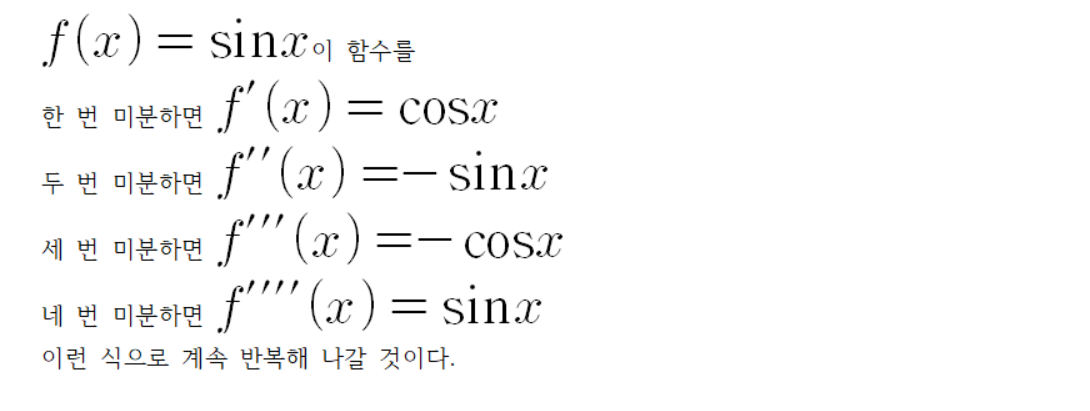
이제 여기서
지수함수 테일러 전개 했던 방식대로
0을 대입해 나가며 개수들을 정의하면
다음과 같이 나올 거다.
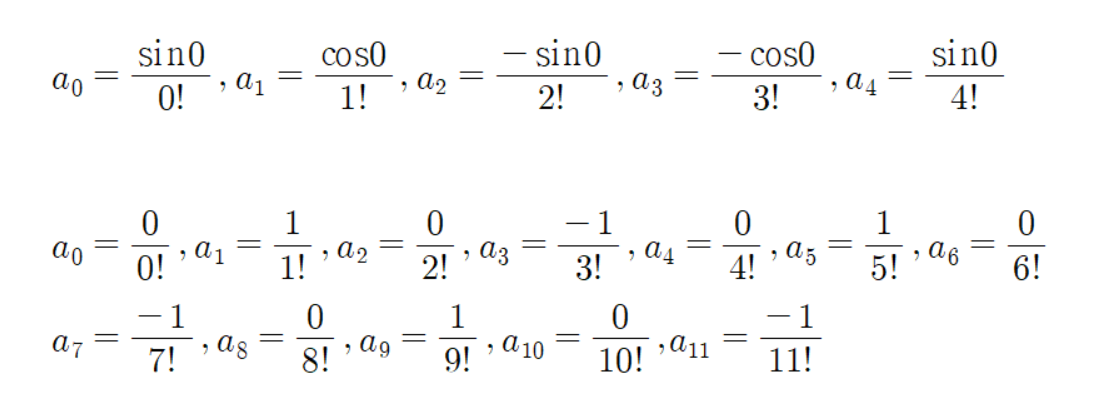
그럼 이 개수들을 처음식에 대입하면 다음과 같은 결과가 나온다.
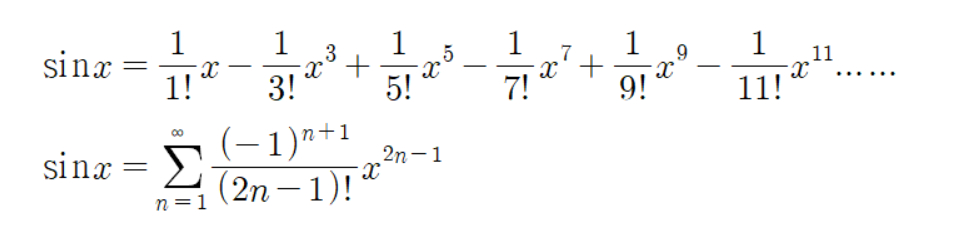
이것이 싸인 함수의 테일러 전개한 결과이다.
같은방식으로 코싸인 함수를 테일러 전개하면 다음과 같은 결과가 나온다.
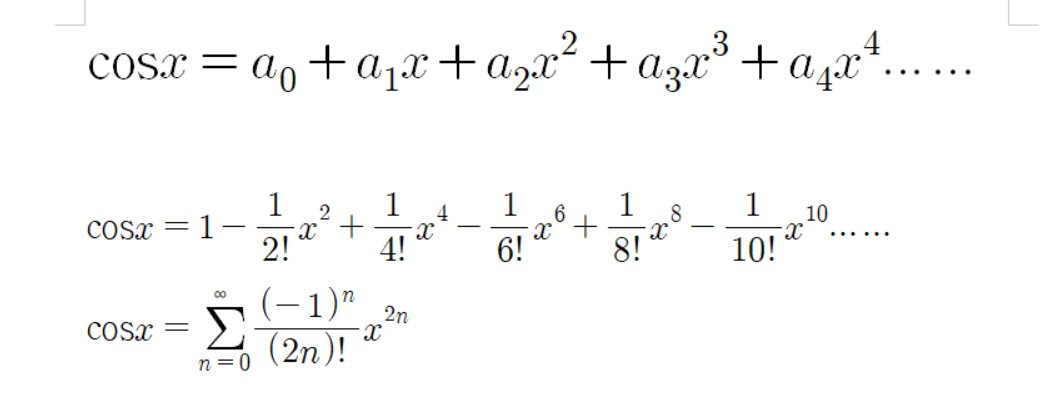
이것이 코싸인 함수를 테일러 전개한 결과이다.
'수학' 카테고리의 다른 글
| 삼각함수 합성공식과 페이저 3편(삼각함수 벡터공간과 복소수 벡터공간의 동형사상) (0) | 2021.11.25 |
|---|---|
| 삼각함수 합성공식과 페이저 2편(삼각함수 집합과 복소수 집합은 벡터공간) (0) | 2021.11.23 |
| 오일러 공식 (0) | 2021.11.22 |
| 삼각함수 합성공식과 페이저 1편 (2) | 2021.11.18 |
| 로그함수 음수구간 (2) | 2021.10.25 |