2024. 6. 9. 15:11ㆍ수학
이번 편은 모든 벡터공간에 기저가 존재함을 증명할 겁니다.
그럼 시작하겠습니다.
이번에 소개할 정리는 다음과 같다.

'선형독립인 극대 부분집합'은 '기저'와 같은 말이다.
그러므로 이 정리가 증명되면 모든 벡터공간에 기저가 존재함을 증명한 것과 같다.
이제 증명해 보자.
위 정리를 증명하기 위해 조른의 원리(조른의 보조정리 라고도 부른다.)를 사용할 거다.
조른의 원리란 다음과 같다.

이 정리는 선형대수학 내용이 아닌 집합론 내용입니다.
집합론을 공부하지 않으신 분들께서는 용어가 생소하실 겁니다.
'사슬'이 무엇인지 '위로 유계'가 무엇인지 '부분순서집합'이 무엇인지 '극대원소'가 무엇인지 에 대한 개념 소개는 조만간 업로드하겠습니다.
그리고 조른의 원리 증명은 생략하겠습니다. (저도 어려워서 잘 모릅니다.ㅠ)
이 원리를 사용하여 증명해 보자.
우선 집합 F을(를) 다음과 같이 정의해 보자.

이러한 집합F에 부분집합이라는 부분순서관계를 논하자.

부분순서관계를 논하는 대상인 집합을 부분순서집합이라 한다.

이 성립한다.
('S을(를) 포함한다' 라는 뜻은 S을(를) 부분집합으로 갖는다는 뜻이다.)
조른의 원리에 의하여
'F의 모든 사슬이 모두 위로 유계임'을 증명하면
'F의 극대원소가 존재함'이 증명되고
동시에 'S을(를) 포함하는 V의 선형독립인 극대 부분집합이 존재함'이 증명되며
동시에 'S을(를) 포함하는 V의 기저가 존재함'이 증명된다.
그러므로
'F의 모든 사슬이 모두 위로 유계임'만 증명하면 증명이 끝난다.
이제 증명해 보자.

이러한 정의에 의하여 상계의 존재 여부를 증명하면 된다.

C은(는) 집합족이다. (집합족이란, 집합들의 집합 이라는 뜻이다.)
그러므로 C의 모든 원소는 집합이다.
상계의 정의에 의해
C의 모든 원소는 U의 부분집합이다.
(참고로 상계의 정의는 부분집합 관계를 말하는 것이 아닙니다.
순서관계를 따지는 말 이므로 오해 말길 바랍니다.
지금과 같은 경우는, 순서관계를 부분집합으로 선택하였으니 이러한 결론이 나옵니다.)
그러므로 다음과 같은 식이 성립한다.

이 식에서 U자리에 어떤 집합X을(를) 대입 하여도 식이 성립하면 X집합은 C의 상계이다.

우선 C이(가) 공집합인 경우에서 C의 상계를 찾아보자.
C이(가) 공집합이면 위 식의 U 자리에 S을(를) 대입하여

이(가) 성립한다.
이유는 다음과 같다.

그러므로 S은(는) C의 상계이다.
그리고 S의 정의와 F의 정의에 의해 S은(는) F의 원소이다.
고로 C이(가) 공집합인 경우, C의 상계 이면서 F의 원소인 U은(는) U=S으로 존재한다.
다시말해, C이(가) 공집합인 경우 C은(는) 위로 유계이다.
이번에는 C이(가) 공집합이 아닌 경우에서 C의 상계를 찾아보자.
우선

이 식에서 U 자리에

을 대입하면

이러한 식이 된다. 이 식은 자명하게 성립한다는 것을 알 수 있다.
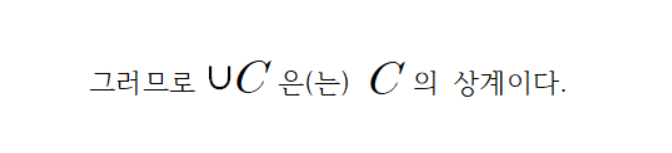
그리고 C은(는) 사슬 이므로

이다.

이므로

이다.
고로 C이(가) 공집합이 아닌 경우, C의 상계 이면서 F의 원소인 U은(는)

으로 존재한다.
다시말해, C이(가) 공집합이 아닌 경우 C은(는) 위로 유계이다.
최종적으로 C이(가) 공집합이든 공집합이 아니든 상관없이
F의 모든 임의의 사슬 C에 대하여 모든 C은(는) 위로 유계이다.
따라서
조른의 원리에 의해 F은(는) 극대 원소가 존재한다.
다시말해

'수학' 카테고리의 다른 글
| 선형대수학 시리즈 16편(선형변환 정의) (0) | 2024.06.16 |
|---|---|
| 선형대수학 시리즈 15편(부분공간과 차원) (0) | 2024.06.10 |
| 행렬 곱의 결합법칙 (2) | 2024.06.07 |
| 직사각형 행렬은 역행렬이 있는가? (0) | 2024.06.04 |
| 행렬 대각성분들의 합의 성질 (0) | 2024.06.04 |