2022. 9. 14. 19:29ㆍ물리
이번 편은 직선 형태의 선 전하로부터 떨어진 위치에 전계를 구해볼 겁니다.
필요한 수학은 고등학교 수학 미적분에 있는
정적분과 급수 내용까지 공부한 실력이라면 충분합니다.
그럼 시작하겠습니다.
우리는 선전하는 모르지만 점 전하는 알고 있다.
수많은 점 전하들이 모여서 직선 형태로 나열된다면 이는 선 전하와 매우 비슷해질 거다.
하지만 조금의 오차가 있을 거다.
이때 점 전하들이 많아지고 더욱 오밀조밀하게 나열된다면
오차는 줄어들 것이다.
먼저 점 전하들의 수를 늘려가며 하나씩 해석해보자.
그러면 규칙을 찾을 수 있을 것이다.
다음과 같이 유한한 길이를 가진 길쭉한 공간 속에 점 전하 1개를 넣었다.

이때 전계의 세기는 다음과 같이 계산된다.

점전하 1개 넣었으므로 전계에다 1을 붙여주자.

여기서 양변에 단위벡터를 곱하여

임을 알 수 있다.
참고로 k는 쿨롱상수이다.

이제 똑같은 상황에서 위 점전하를 3개로 쪼개어 일정한 간격으로 배치하였다.
전하량 또한 3등분으로 쪼게어졌고,
전하량 총 량은 일정하다.

이때 전계의 세기는 얼마일까?
3개의 전하가 주는 각각의 전계 벡터의 합이
최종 전계 벡터이다.

중심 전계는 다음과 같이 계산된다.

위와 아래 전계는 어떡해 구할까?
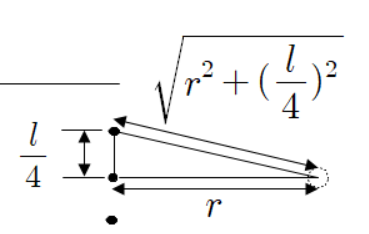
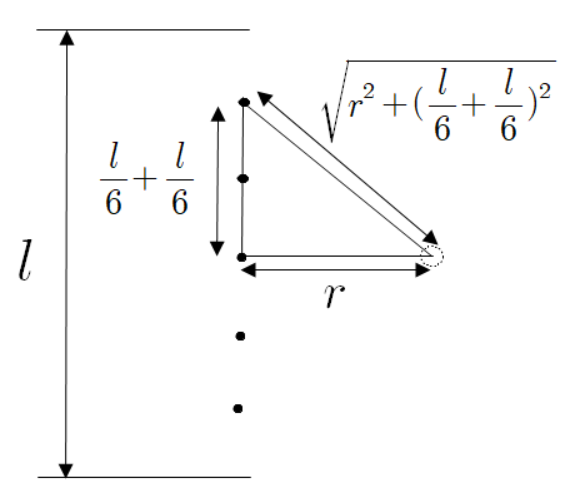
위쪽에 배치된 점전하와 떨어진 거리는 다음과 같이 피타고라스 정리를 활용하여 구한다.
위 전계 벡터와 아래 전계 벡터를 비교했을때
크기는 같고 방향만 다르다.
이를 수식으로 쓰면 다음과 같다.
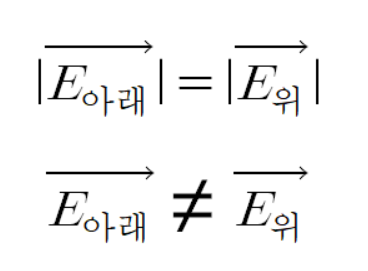
그리고 크기 값은 다음과 같다.

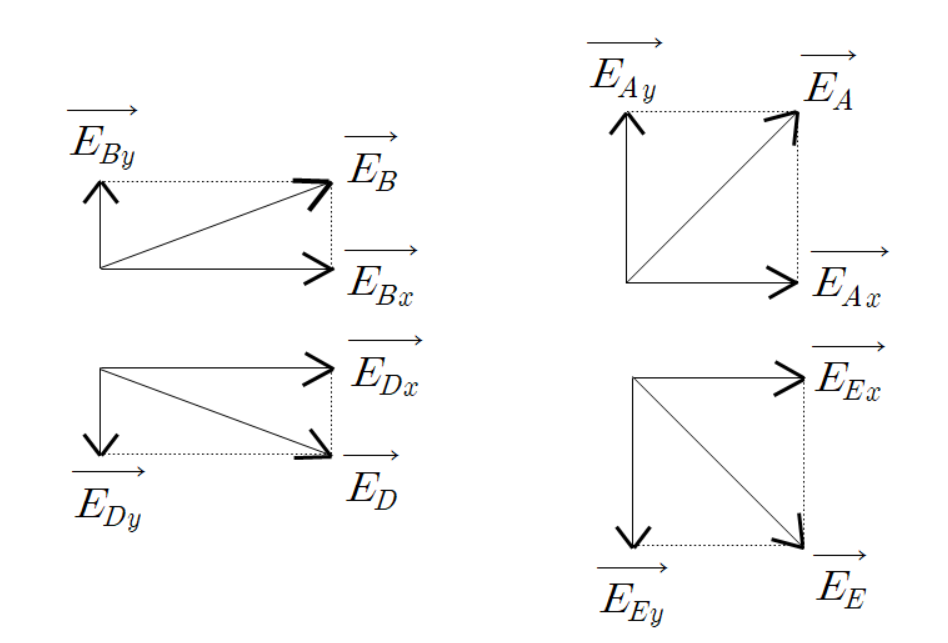
위 전계 벡터는 다음과 같이 수평성분과 수직성분으로 분할하여 볼 수 있다.
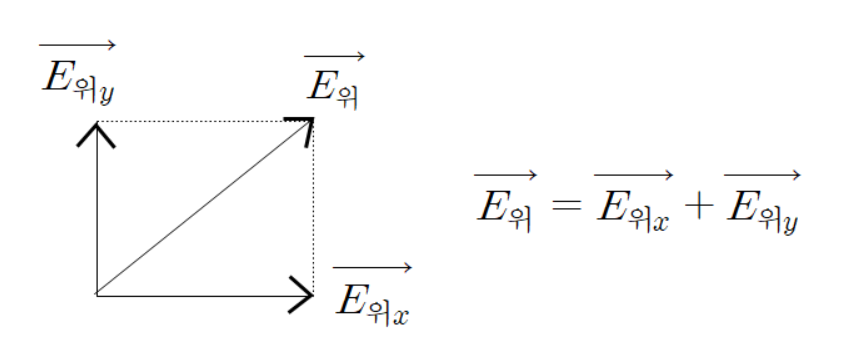
아래 전계 벡터또한 다음과 같이 수평성분과 수직성분으로 분할하여 볼 수 있다.
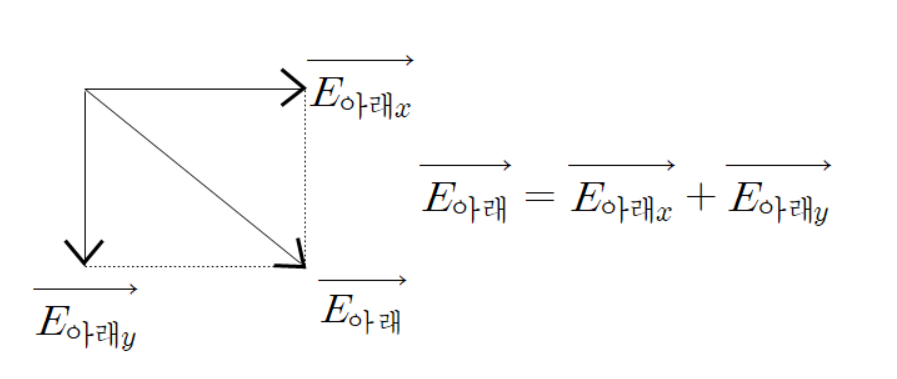
위 전계 벡터와 아래 전계 벡터는 수평을 기준으로 대칭이기 때문에
다음과 같은 식이 성립한다.
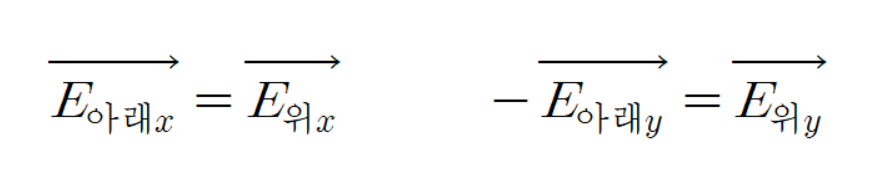
이 식을 이용하여 위 전계와 아래 전계를 더하면 다음과 같다.
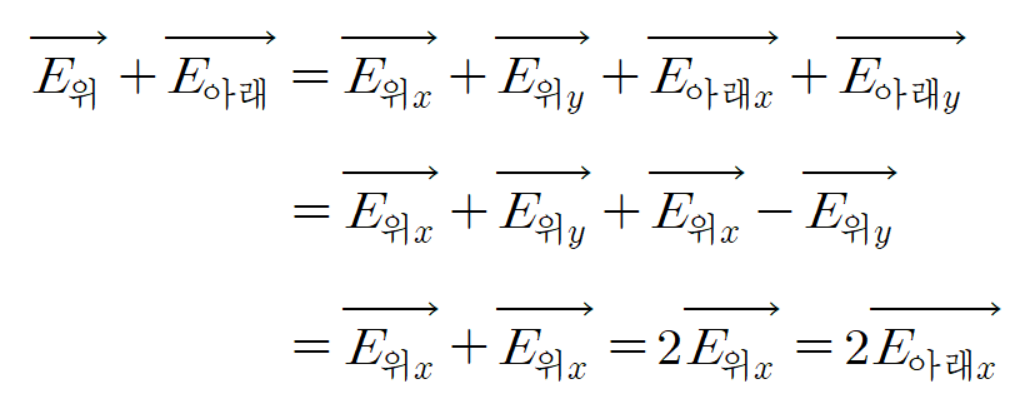
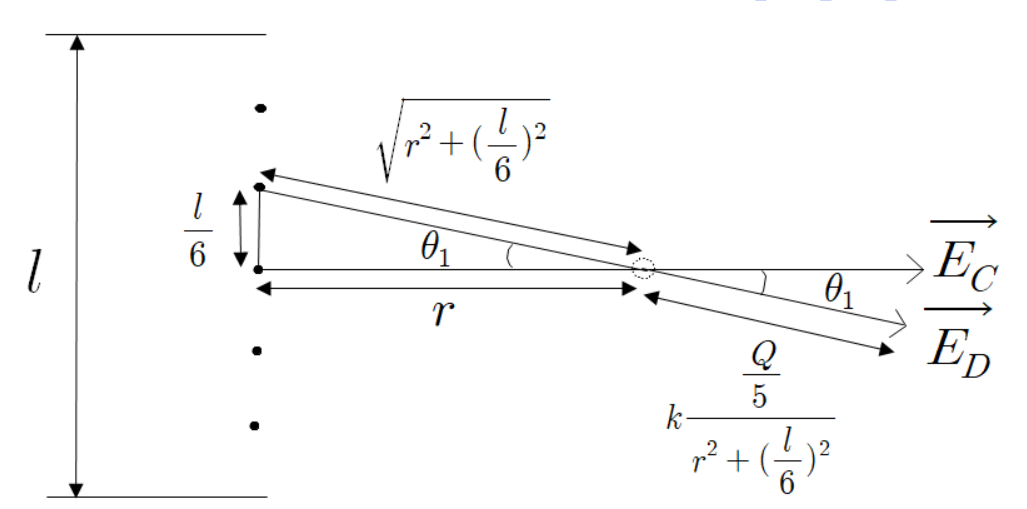
여기서 부터 기하적으로 접근해보자.
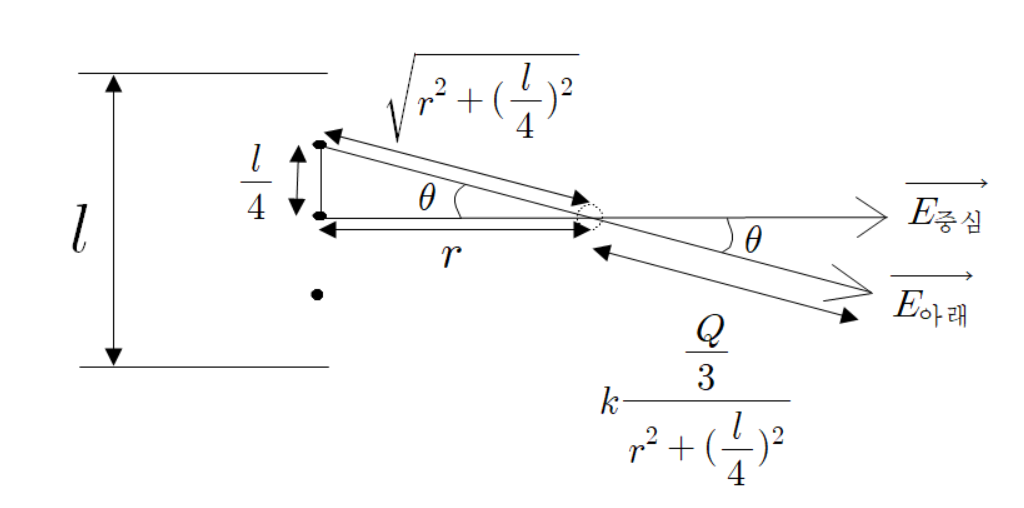
이 그림을 통해
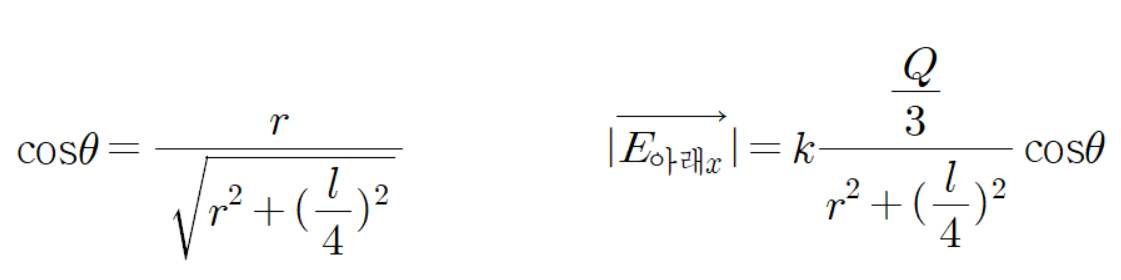
임을 알 수 있다.
그러므로
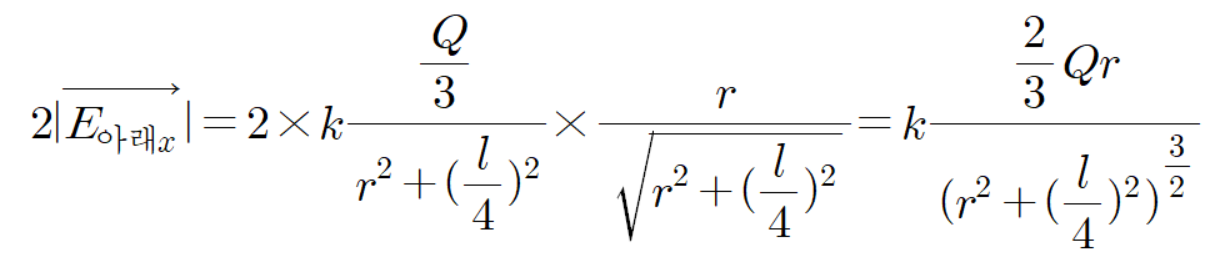
이고
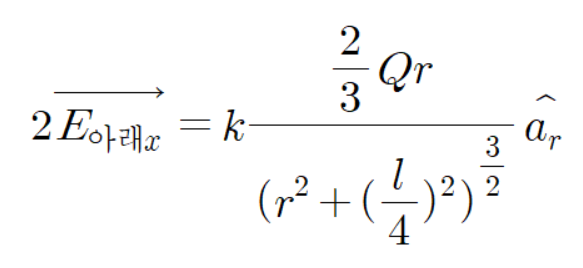
이렇게 된다는 것을 알 수 있다.
따라서
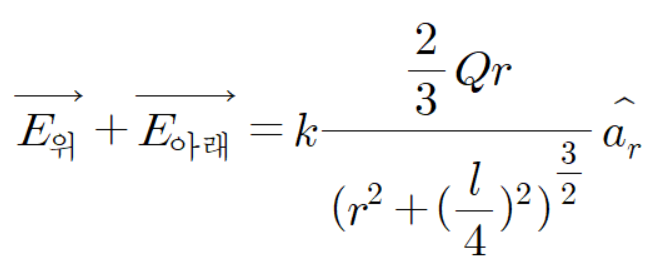
이므로
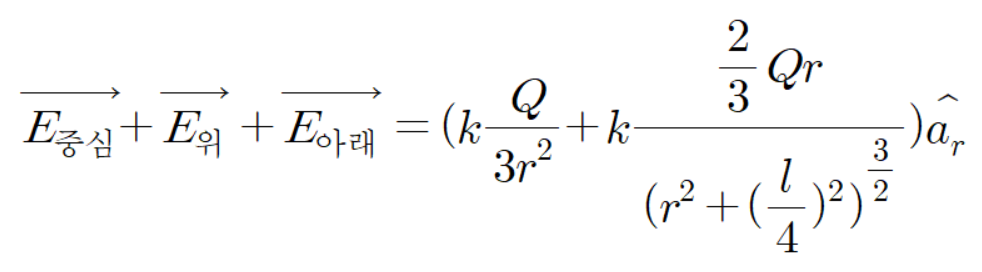
된다.
그렇기에

임을 알 수 있다.
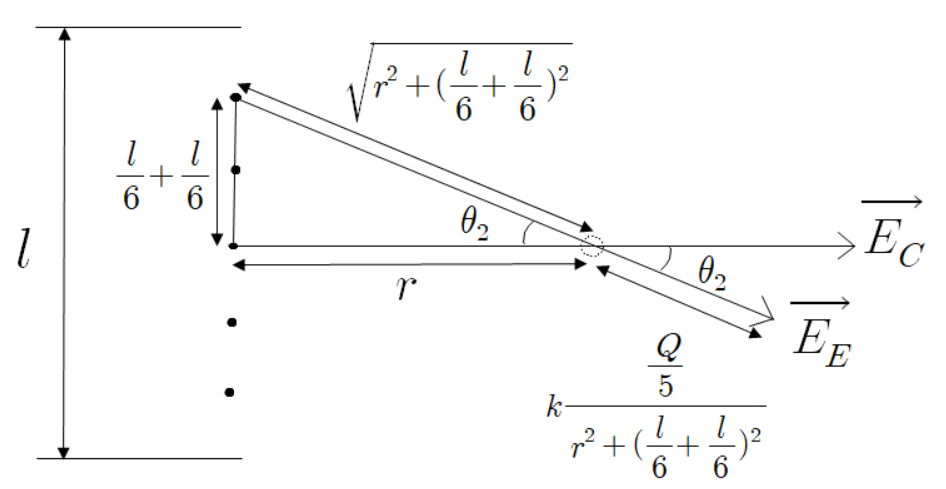
이제 점전하 5개의 상황을 보자.
다음과 같이 아까와 똑같은 조건에서 점전하 5개를 놓았다.
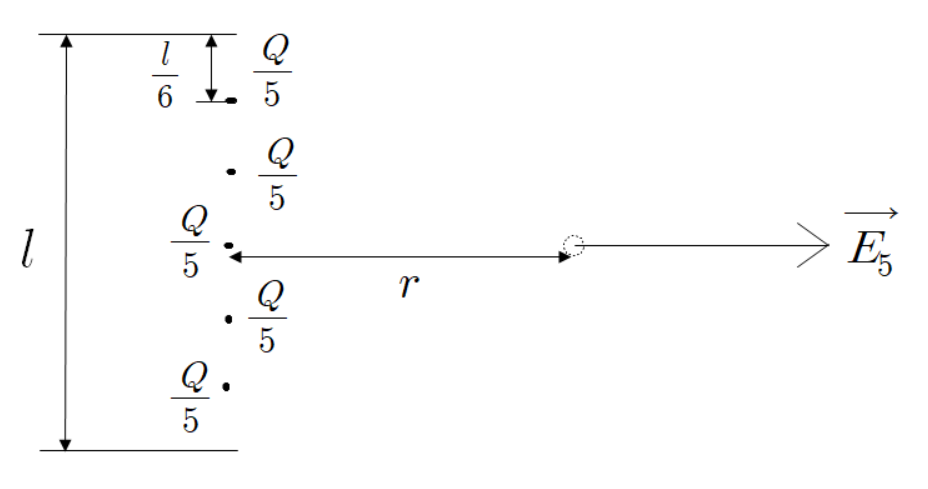
역시나 점전하의 간격은 일정하다.
위에서 했던 방법 그대로 계산하면 된다.
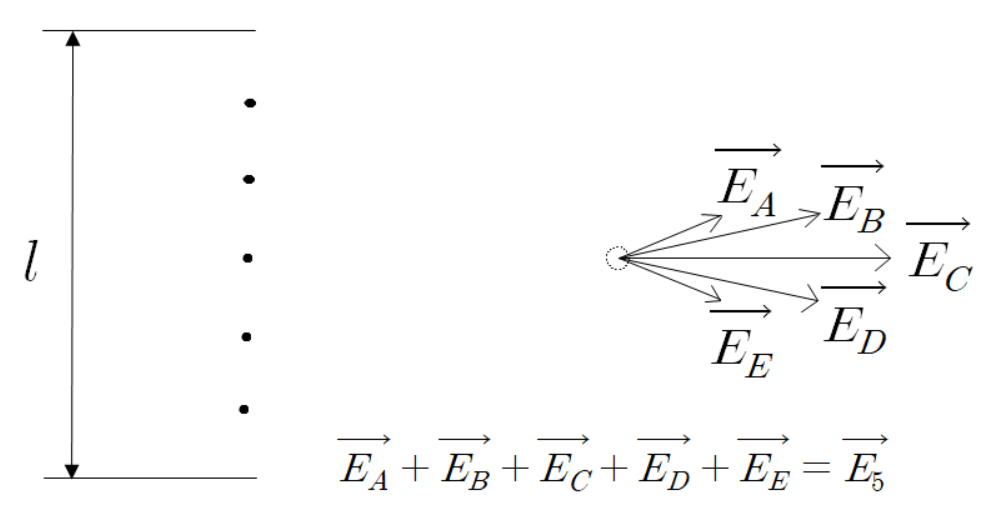
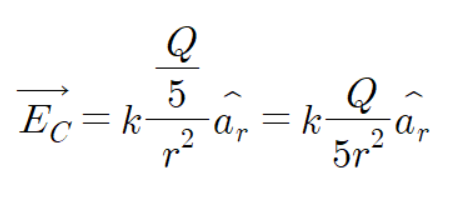
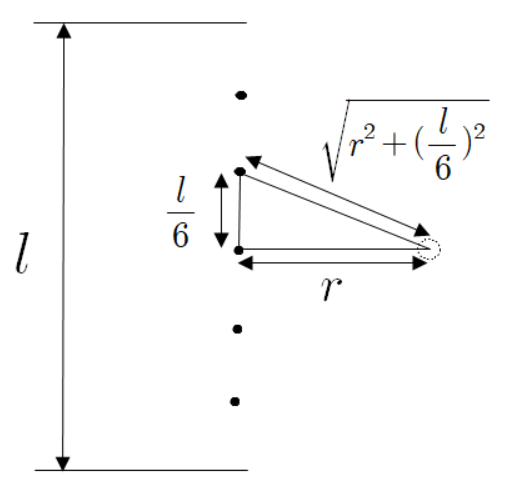
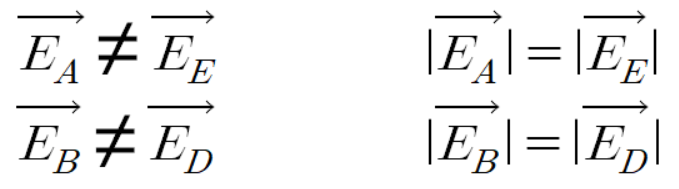
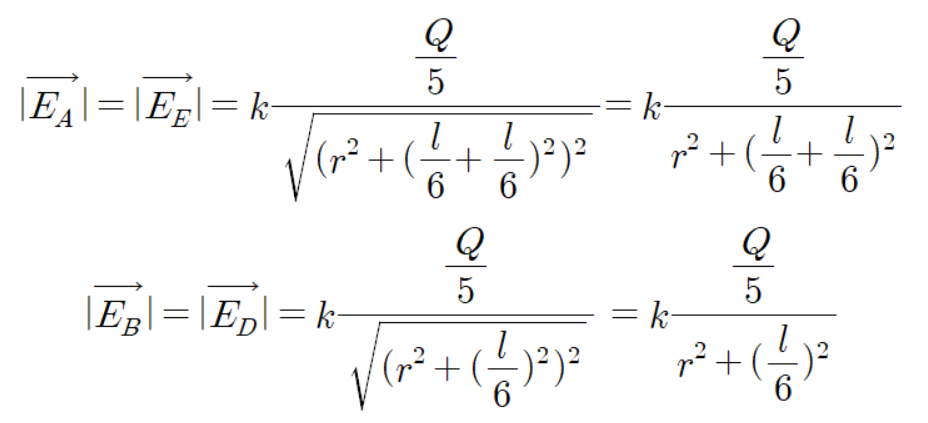
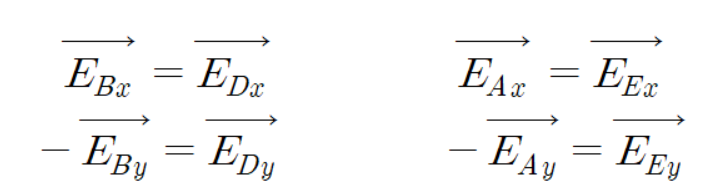
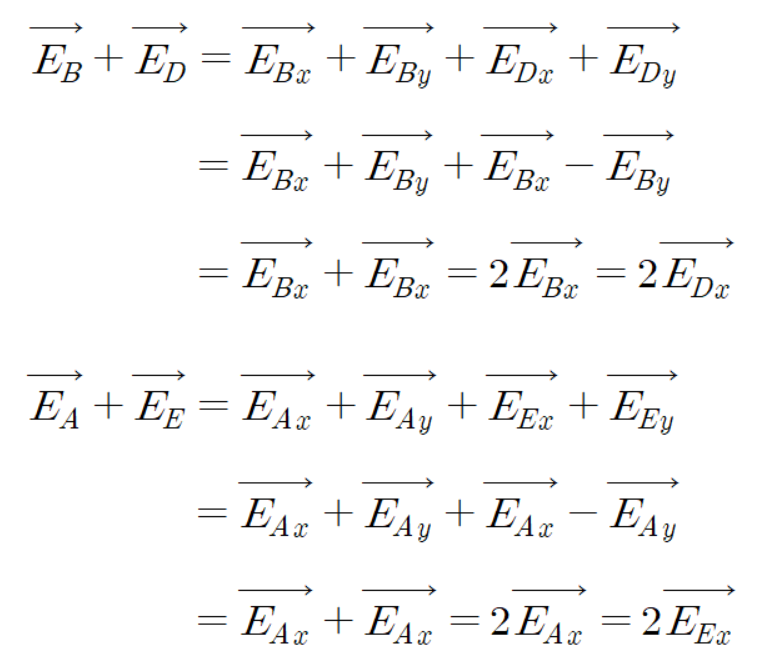
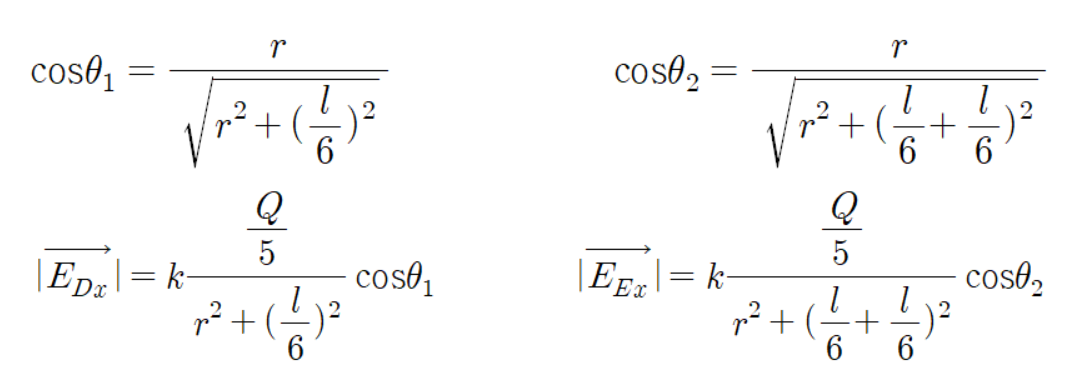
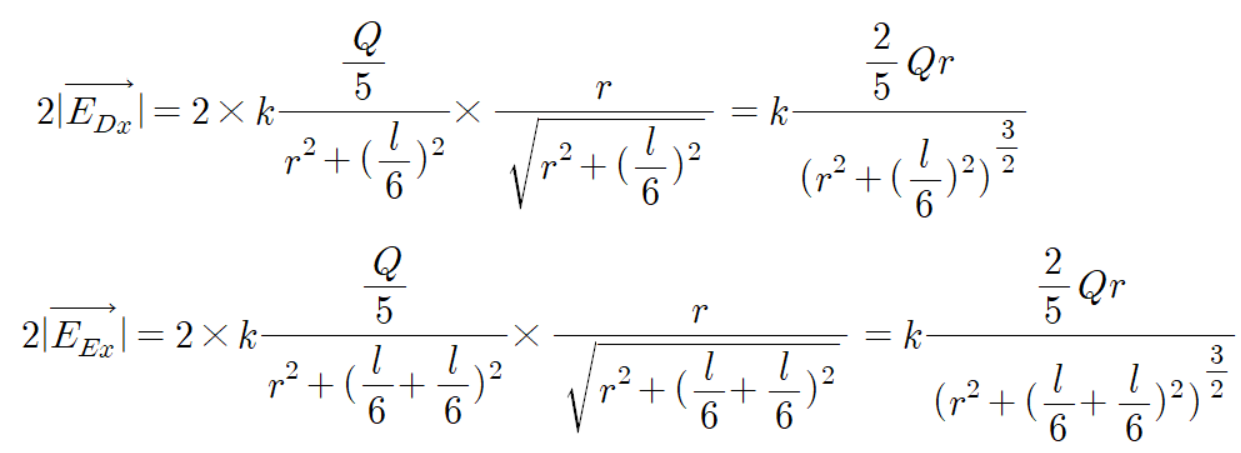
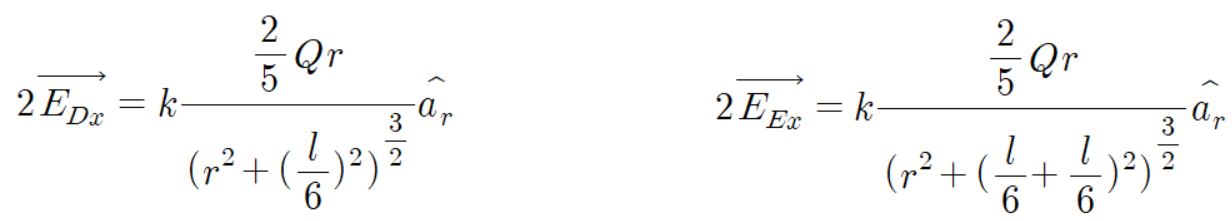
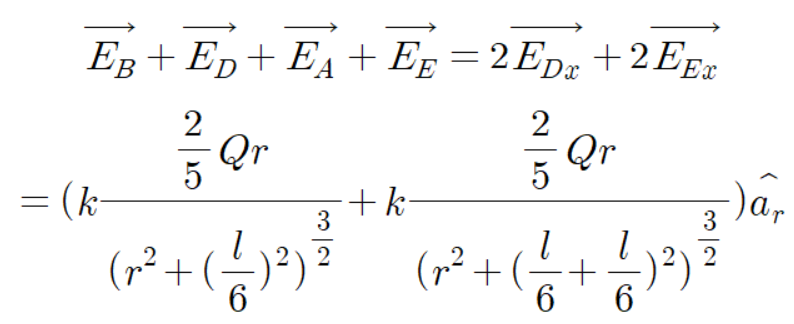
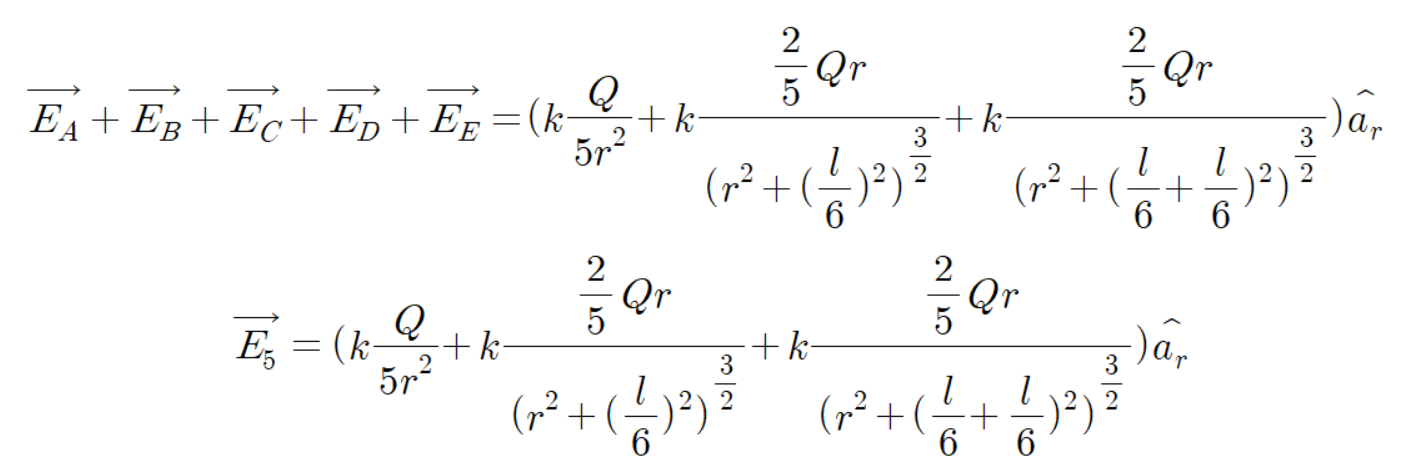
이제 점전하 7개를 알아보자.
7개 또한 위와 똑같은 방법으로 하면 된다.
7개 부터는 결과식만 보자.
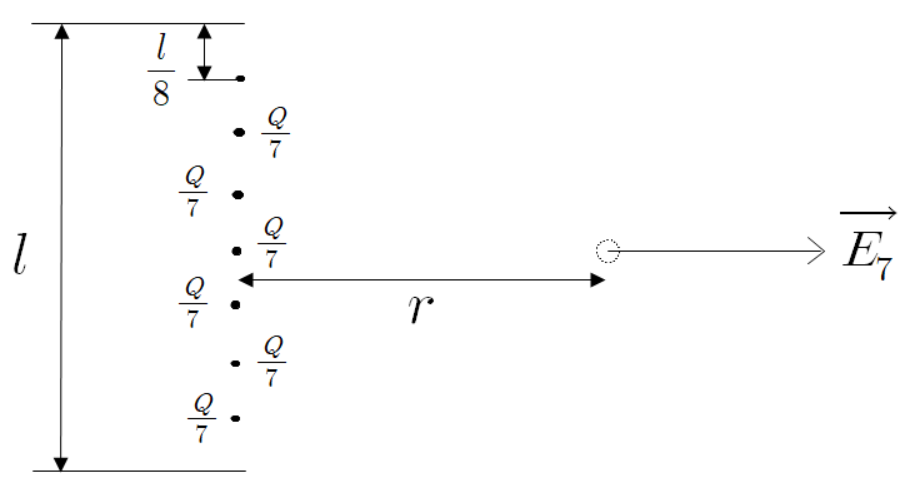
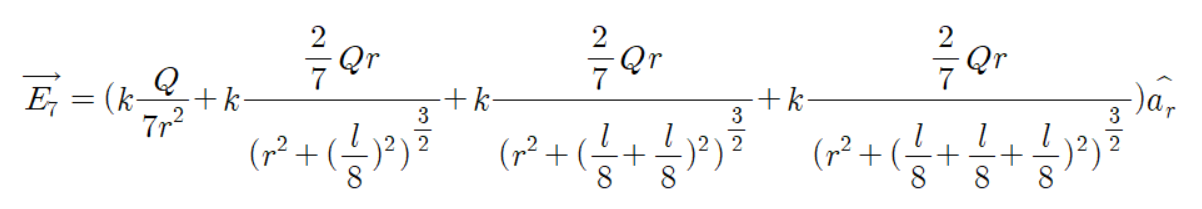
이제 규칙이 좀 보이기 시작한다.
지금까지의 결론을 모두 모아보면 다음과 같다.

이 수열의 일반항은 다음과 같다.
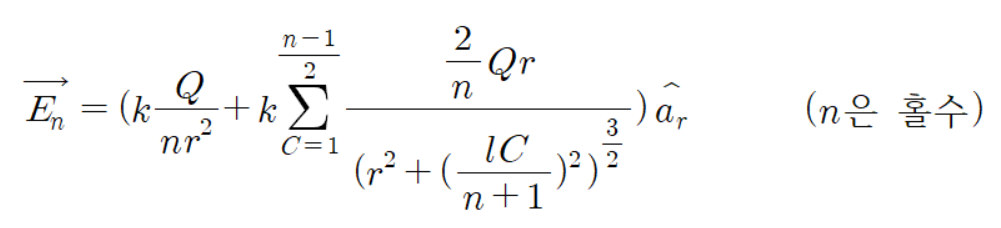
이제 이 수열을 무한대로 극한을 보내면 선전하 공식이 나온다.
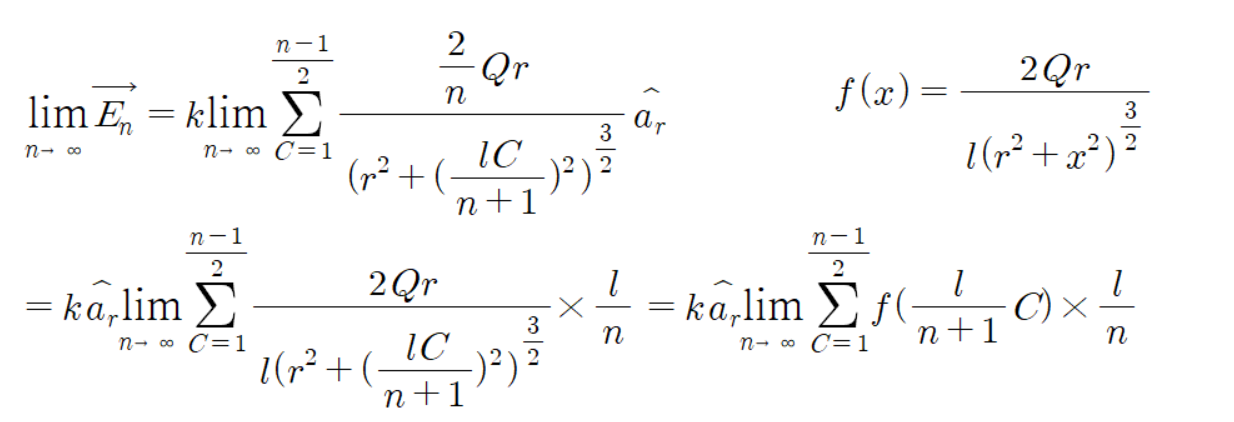
n이 (무한대로 가므로) 어차피 큰 수가 되어 버리니 n+1과 n-1은 n으로 퉁칩시다!!
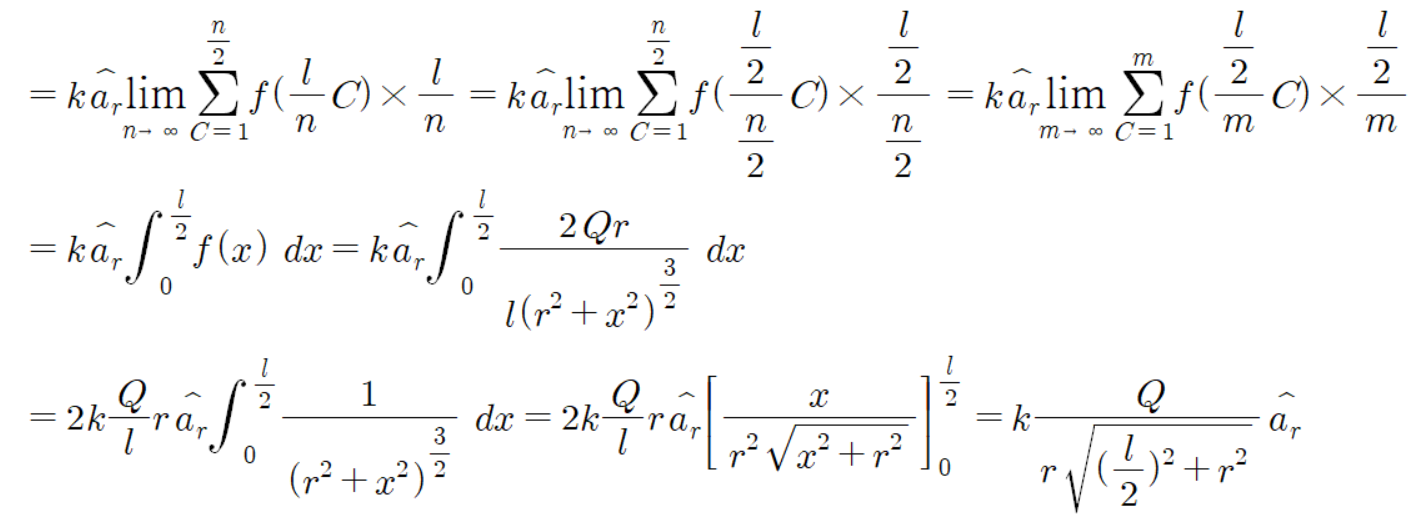
이것이 선전하 공식이다.
참고로 적분이 저렇게 나왔다는 것에 대한 증명은 아래와 같다.
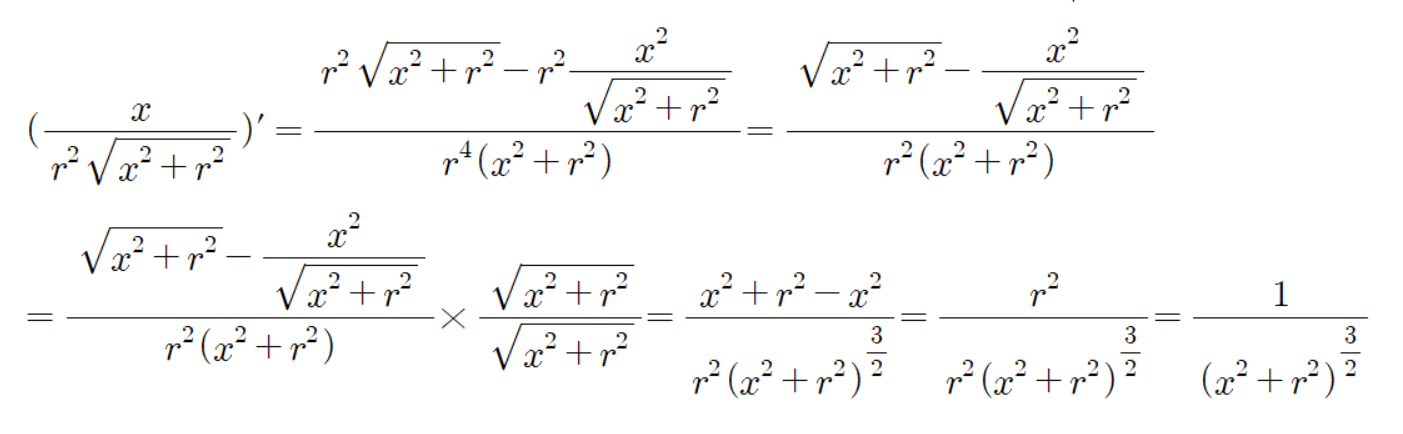
치환적분으로 시도해보았으나 도저히 안되서 이렇게 역 연산 과정으로 증명했습니다.
우리가 구한 유한 선전하 공식을 보자.
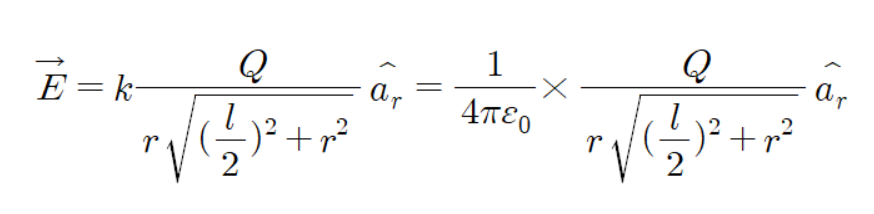
여기에 길이를 무한대로 보내면 무한 선전하 공식이 된다.

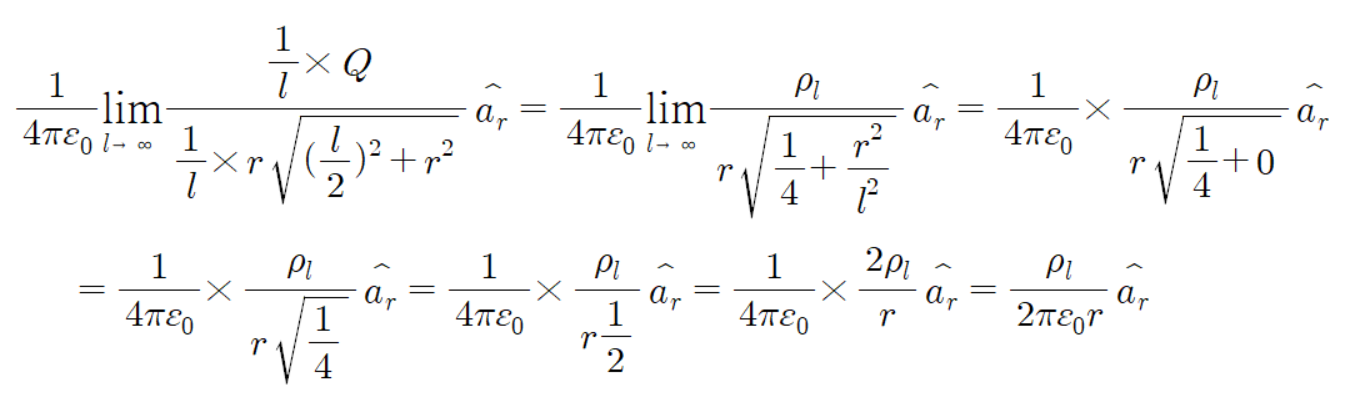
따라서 무한 선전하 로부터의 전계 공식은 다음과 같다.
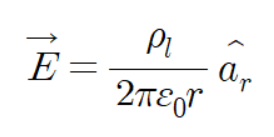
'물리' 카테고리의 다른 글
| 등온과정 (0) | 2022.08.29 |
|---|---|
| 단열과정 (0) | 2022.08.28 |
| 등압과정 (0) | 2022.08.01 |
| 로렌츠 변환으로 계산한 속도의 덧셈 공식 (0) | 2022.07.10 |
| 입자 가속기의 시간-속도 그래프 (0) | 2022.06.27 |