선형대수학 시리즈 17편(영공간과 상공간은 부분공간)
2024. 6. 18. 17:49ㆍ수학
이번 편은 영공간과 상공간이 부분공간인가에 대한 증명을 해볼 겁니다.
그럼 시작하겠습니다.
이번에 소개할 정리는 다음과 같다.
우선 다음과 같이 몇 가지를 정의 하자.

이를 바탕으로 다음과 같이 영공간과 상공간을 정의 하자.

그리고 이러한 정의들을 바탕으로 소개할 정리는 다음과 같다.

이제 증명해 보자.
N(T)은(는) 벡터 합에 대해 닫혀있다.
이에 대한 증명은 다음과 같다.

N(T)은(는) 스칼라 곱에 대해 닫혀있다.
이에 대한 증명은 다음과 같다.

N(T)은(는) V의 영벡터를 포함한다.
이에 대한 증명은 다음과 같다.

N(T)은(는)
벡터 합에 대해 닫혀있고
스칼라 곱에 대해 닫혀있으며
V의 영벡터를 포함하므로
N(T)은(는) V의 부분공간이다.
R(T)은(는) 벡터 합에 대해 닫혀있다.
이에 대한 증명은 다음과 같다.

R(T)은(는) 스칼라 곱에 대해 닫혀있다.
이에 대한 증명은 다음과 같다.

R(T)은(는) W의 영벡터를 포함한다.
이에 대한 증명은 다음과 같다.
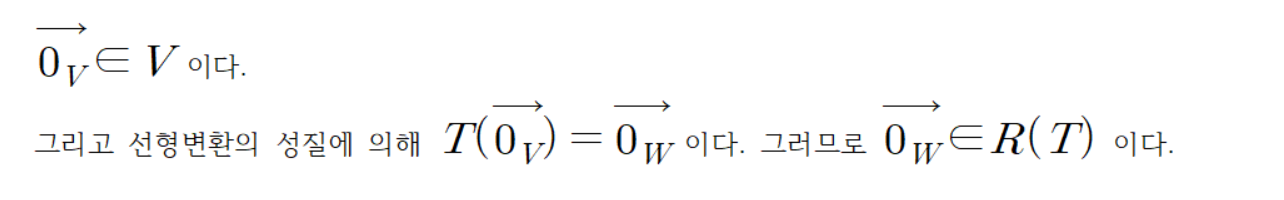
R(T)은(는)
벡터 합에 대해 닫혀있고
스칼라 곱에 대해 닫혀있으며
W의 영벡터를 포함하므로
R(T)은(는) W의 부분공간이다.
'수학' 카테고리의 다른 글
| 선형대수학 시리즈 18편(상공간과 기저의 관계) (0) | 2024.06.19 |
|---|---|
| 선형대수학 시리즈 0편(벡터공간이란 무엇인가?) (0) | 2024.06.19 |
| 선형대수학 시리즈 16편(선형변환 정의) (0) | 2024.06.16 |
| 선형대수학 시리즈 15편(부분공간과 차원) (0) | 2024.06.10 |
| 행렬 곱의 결합법칙 (2) | 2024.06.07 |