선형대수학 시리즈 5편

 

 

 

이번 편은 생성공간에 대한 기본적인 정리를 알아보겠습니다.

 

선형대수학 시리즈 4편은https://pilgigo.tistory.com/entry/%EC%84%A0%ED%98%95%EB%8C%80%EC%88%98%ED%95%99-%EC%8B%9C%EB%A6%AC%EC%A6%88-4%ED%8E%B8-%EB%B6%80%EB%B6%84%EA%B3%B5%EA%B0%84-%EA%B5%90%EC%A7%91%ED%95%A9-%EC%A0%95%EB%A6%AC

선형대수학 시리즈 4편 부분공간 교집합 정리

여기를 참고해 주세요.

 

그럼 시작하겠습니다.

 

 

이번 편에 소개할 정리는 다음과 같다.

 

벡터공간 V에 대하여 다음 두 정리가 성립한다. 

 

 

 

 

이제 증명해 보자.

 

F을(를) '체' 라 정의하고 첫 번째 정리와 두 번째 정리를 증명하자.

 

첫 번째 정리의 증명은 다음과 같다.

먼저

이다.

이들은 모두 일차결합의 형태이므로 span의 정의에 의해

이제 span(S)이(가) V의 부분공간임을 증명해 보자.

어떤 집합이 부분공간인지 판별하는 방법은 선형대수학 시리즈 3편(부분공간)에서 설명한 방법대로 하면 된다.

선형대수학 3편은  

선형대수학 시리즈 3편 (부분공간)

여기를 참고해 주세요.

그러면

이므로

이다.

이 또한 일차결합의 형태 이므로 span의 정의에 의해

이다.

따라서

그리고

이 또한 일차결합의 형태 이므로 span의 정의에 의해

이다.

따라서

그리고

 

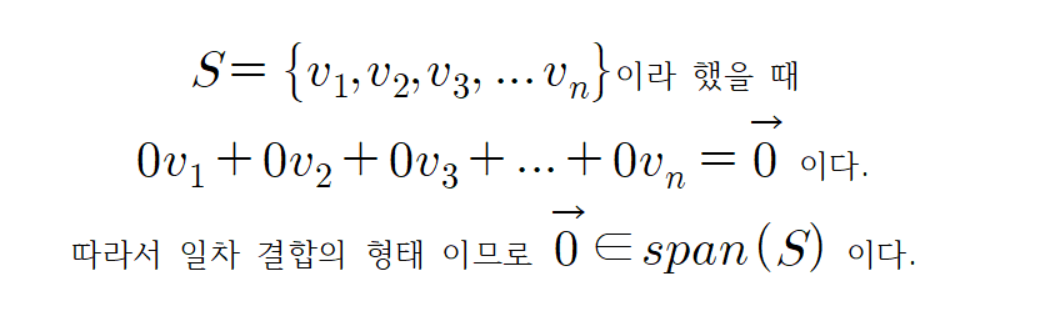
정리하여 span(S)은(는) 벡터 합에 대해 닫혀 있고 스칼라 곱에 닫혀 있으며 영벡터를 가지고 있다.

고로 span(S)은(는) V의 부분공간이다. 

 

 

 

 

 

두 번째 정리의 증명은 다음과 같다.

이다.

그러므로 집합S의 모든 원소들의 모든 임의의 스칼라들에 대한 모든 일차 결합에 대하여

따라서

증명 끝.

 

 

6편이 궁금하신 분들께서는 https://pilgigo.tistory.com/entry/%EC%84%A0%ED%98%95%EB%8C%80%EC%88%98%ED%95%99-%EC%8B%9C%EB%A6%AC%EC%A6%88-6%ED%8E%B8

선형대수학 시리즈 6편

여기를 참고해 주세요.