2025. 3. 20. 17:56ㆍ수학
이번 편은 행렬의 특성다항식 차수를 알아보고
그럼 시작하겠습니다.

이번에 소개할 정리는 다음과 같다.

이제 증명해 보자.
먼저 행렬 A 의 특성다항식이 n 차 다항식 이라는 것부터 증명해 보자.
이를 증명하기 위해
수학적 귀납법으로 증명하기 위해

라는 사실을 증명하고

라는 사실을 증명하면 된다.
먼저

이 명제부터 증명해 보자.

그러면 특성다항식의 정의에 의해

이다.
그러므로

이다.
따라서

증명 끝.
이제

라는 사실을 증명해 보자.

그리고

그러면 특성다항식 이라는 개념의 정의에 의해

이다.
그리고

그러면



(참고로 이 계산은 여인수 전개한 꼴이다.)
여기서


이(가) 성립한다.
그러므로 특성다항식의 정의에 의해

그리고

라는 명제가 성립함을 가정하였으므로

정리하여

임을 알 수 있다.
여기서

보다시피 자명하게 독립변수 t 의 차수 값이 k-1 을(를) 초과 할 수 없는 꼴이다.
고로
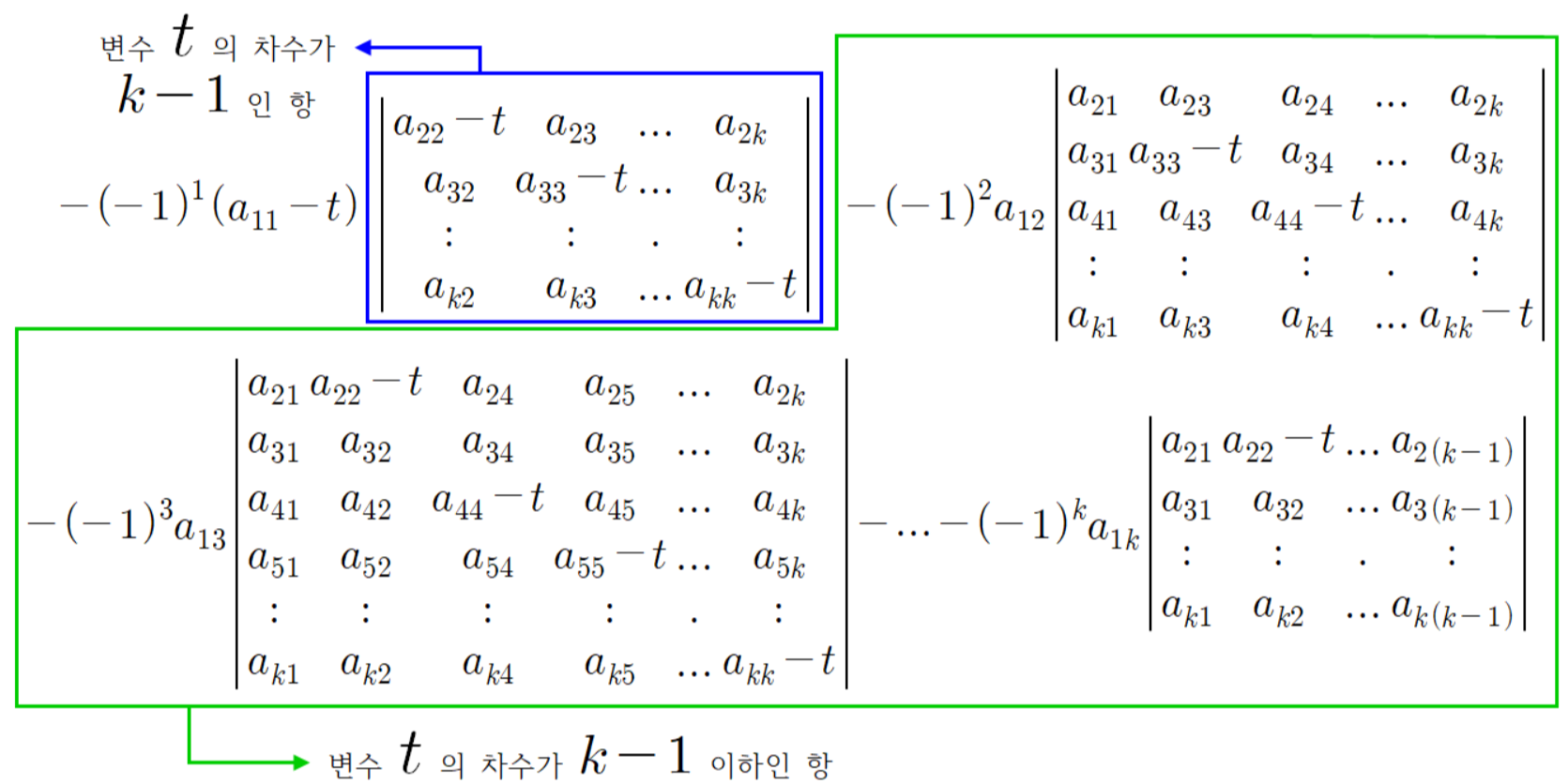
임을 알 수 있다.
따라서

이로써 증명이 끝났다.
최종적으로 정리하여

라는 명제가 성립함을 증명하였고,

라는 명제가 참이면

라는 명제도 참임을 증명하였으므로
수학적 귀납법에 의해

행렬 A 의 특성다항식이 n 차 다항식임에 대한 증명이 끝났다.
이러한 사실을 이용하여 귀류법을 통해

라는 사실을 증명해 보자.
먼저 모든 임의의 자연수 n 에 대하여

그러면

따라서 귀류법에 의해
모든 임의의 자연수 n 에 대하여

이는 다시말해

행렬 A 에 대한 행과 열의 개수는 n 개 라는 증명이 끝났다.
이제 최고차항의 계수를 알아보자.
이는 연역적으로 증명해 보자.

그러면 이러한 특성다항식은 위에서 했던 방법대로 똑같이 계산하여

임을 알 수 있다.
여기서


이므로
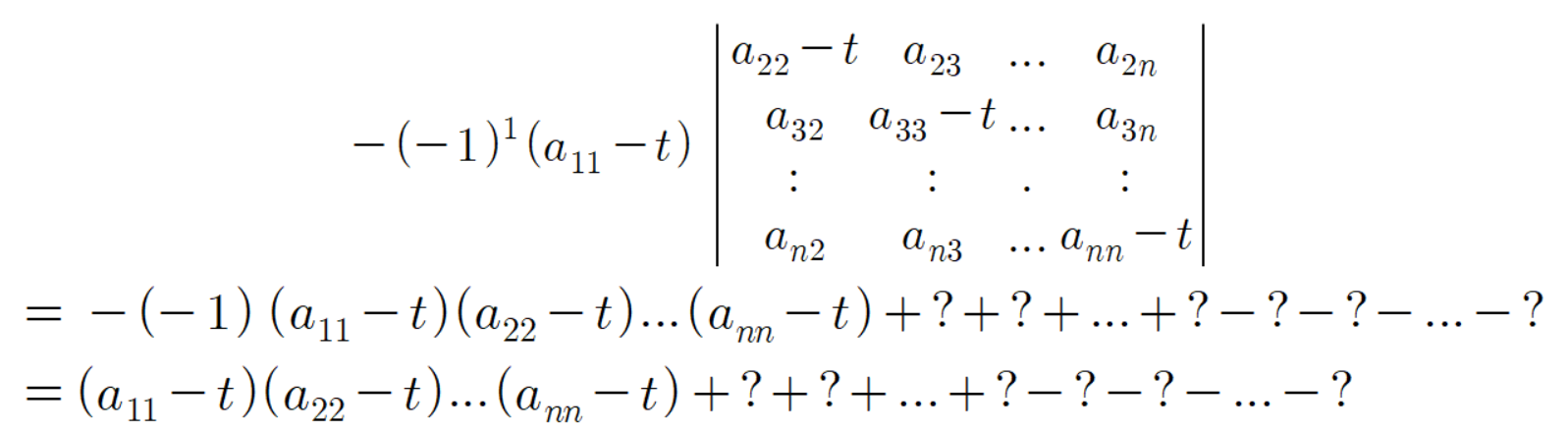
이다.
여기서

이므로 다항식
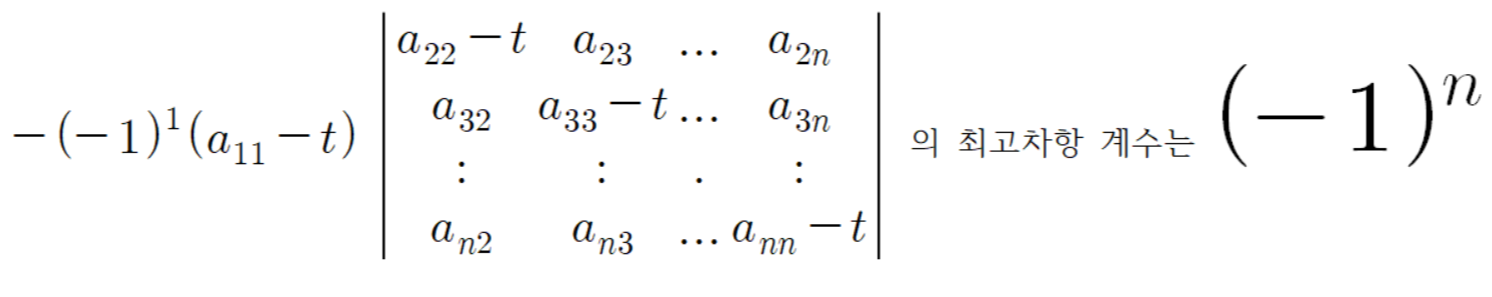
이다.
그러므로 다항식

의 최고차항 계수는

이다. (단, 이 다항식의 독립변수는 t 이고 나머지 문자는 상수이다. 그리고 t 은(는) 체 F 의 원소이다.)
따라서

'수학' 카테고리의 다른 글
| 선형대수학 시리즈 55편(선형연산자의 고윳값과 행렬의 고윳값의 관계) (0) | 2025.03.28 |
|---|---|
| 선형대수학 시리즈 54편(행렬의 고유벡터가 될 필요충분조건) (0) | 2025.03.25 |
| 선형대수학 시리즈 51편(행렬의 고윳값이 될 필요충분조건) (0) | 2025.03.13 |
| 선형연립일차방정식 계수행렬이 가역 또는 비가역이 될 필요충분조건 (1) | 2025.03.12 |
| 동차선형연립방정식의 해집합은 좌측곱 변환의 영공간 (0) | 2025.03.11 |