2024. 5. 5. 23:10ㆍ수학
이번 편은 생성공간에 대한 기본적인 정리를 알아보겠습니다.
선형대수학 시리즈 4편은
선형대수학 시리즈 4편 부분공간 교집합 정리
안녕하신가?이번 편은 두 부분공간의 교집합이 부분공간일 수 있는지에 대한 정리를 증명해 보겠소. 그럼 시작하오. 아직 부분공간에 대해 깨우치지 못한 자는 https://pilgigo.tistory.com/entry/%
pilgigo.tistory.com
여기를 참고해 주세요.
그럼 시작하겠습니다.
이번 편에 소개할 정리는 다음과 같다.

이제 증명해 보자.
첫 번째 명제의 증명은 다음과 같다.

이다.
그리고 span(S) 이(가) V 의 부분공간임을 증명해 보자.

그러므로
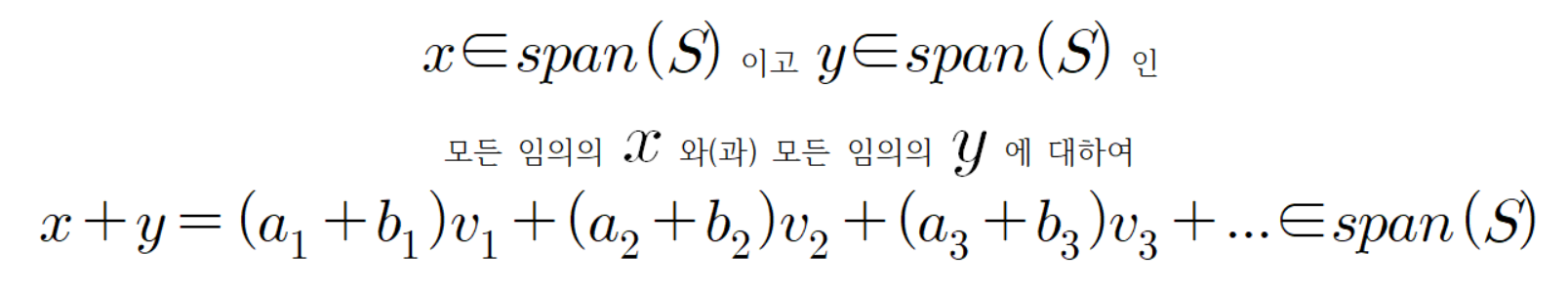
이다.
따라서 벡터합에 대하여 닫혀있다.
그리고
span 의 정의에 의해 스칼라곱에 대하여도 닫혀있고 영벡터 또한 표함한다.
고로 부분공간 필요충분조건에 의해 span(S) 은(는) V 의 부분공간이다.
부분공간 필요충분조건은
선형대수학 시리즈 3편 (부분공간)
이번 편은 부분공간에 대해 알아 보겠습니다. 그럼 시작하겠습니다. 우선 '부분공간' 개념을 정의해 보자. 벡터공간 V의 어떤 부분집합이, 부분공간임을 식별하는 방법이
pilgigo.tistory.com
여기를 참고해 주세요.
두 번째 명제의 증명은 다음과 같다.
위에서 증명한 첫 번째 명제에 의해 span(S) 은(는) W 의 부분공간이다.
W 의 부분공간은 기본적으로 W 의 부분집합이므로 span(S) 은(는) W 의 부분집합이다.
다음 편은
선형대수학 시리즈 6편
이번 편은 선형종속과 선형독립에 관한 기본적이고 쉬운 정리 하나를 소개하겠습니다. 그럼 시작하겠습니다. 이번에 알아볼 정리는 다음과 같다.1.에 대한 증명은 다음과 같다.2.에 대한 증
pilgigo.tistory.com
여기를 참고해 주세요.
'수학' 카테고리의 다른 글
| 선형대수학 시리즈 8편 (기저) (0) | 2024.05.09 |
|---|---|
| 선형대수학 시리즈 6편 (0) | 2024.05.08 |
| 선형대수학 시리즈 4편(부분공간 교집합) (0) | 2024.05.02 |
| 선형대수학 시리즈 3편 (부분공간) (0) | 2024.05.01 |
| 선형대수학 시리즈 2편(항등원과 역원 정리) (0) | 2024.04.20 |