2024. 10. 12. 15:29ㆍ수학
이번 편은 동형사상이 존재할 필요충분조건을 알아볼 겁니다.
그럼 시작하겠습니다.
이번에 소개할 정리는 다음과 같다.
이제 증명해 보자.
필요충분조건을 증명하는 것 이므로 다음 두 명제를 증명해 보자.
첫 번째 명제의 증명은 다음과 같다.
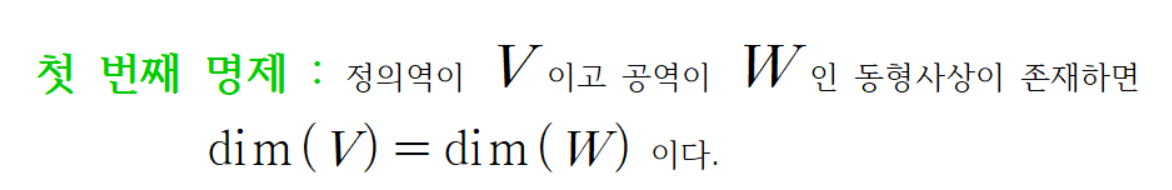
이에 대한 증명은
선형대수학 시리즈 20편(영공간과 단사함수 동치관계)
이번 편은 선형변환이 단사함수인 경우와 영공간의 관계를 알아볼 겁니다. 그럼 시작하겠습니다. 이번에 소개할 정리는 다음과 같다. 이제 증명해 보자. 이 명제의 증명은 다
pilgigo.tistory.com
여기를 참고해 주세요.
그러므로
이다.
차원정리는
선형대수학 시리즈 19편(차원정리)
이번 편은 차원정리를 알아볼 겁니다. 그럼 시작하겠습니다. 차원정리는 다음과 같다. 이제 증명해 보자.N(T) 이(가) V의 부분공간 이라는 증명은 선형대수학 시리즈 16편(영공간과 상공간은
pilgigo.tistory.com
여기를 참고해 주세요.
따라서
이다.
첫 번째 명제의 증명이 끝났다.
두 번째 명제를 증명해 보자.
이에 대한 증명은
선형대수학 시리즈 30편(기저와 대응되는 모든 경우에서 선형변환 정의 가능성)
이번 편은 기저와 대응되는 모든 경우에서 선형변환 정의 가능성에 대해 알아볼 겁니다. 그럼 시작하겠습니다. 정리를 소개하기 전 다음과 같은 기호를 정의하자. 이번에 소개할 정
pilgigo.tistory.com
여기를 참고해 주세요.
이에 대한 증명은
선형대수학 시리즈 21편(차원이 같은 경우 전사와 단사 동치관계)
이번 편은 같은 차원인 두 유한차원 벡터공간의 선형변환이 단사임과 전사임이 동치관계 인가를 알아볼 겁니다. 그럼 시작하겠습니다. 이번에 소개할 정리는 다음과 같다. 참고로 이
pilgigo.tistory.com
여기를 참고해 주세요.
고로 T은(는) 전단사 함수이고 동형사상이다.
'수학' 카테고리의 다른 글
| 공리계와 여러 성질들 용어 정의(무모순성과 독립성) (0) | 2024.10.26 |
|---|---|
| 선형대수학 시리즈 32편(역사상과 역행렬) (0) | 2024.10.14 |
| 선형대수학 시리즈 30편(기저와 대응되는 모든 경우에서 선형변환 정의 가능성) (0) | 2024.10.11 |
| 선형대수학 시리즈 29편(선형변환 합성 행렬표현) (0) | 2024.10.07 |
| 선형대수학 시리즈 28편(역사상) (2) | 2024.10.04 |