2024. 10. 14. 23:10ㆍ수학
이번 편은 선형변환이 가역이될 필요충분조건을 선형변환 행렬표현 식으로 알아볼 겁니다.
그럼 시작하겠습니다.
이번에 소개할 정리는 다음과 같다.

이제 증명해 보자.
필요충분조건을 증명하는 것이므로 다음 두 명제를 증명하면 된다.

첫 번째 명제의 증명은 다음과 같다.

이다.
이에 대한 증명은
선형대수학 시리즈 31편(동형사상 필요충분조건)
이번 편은 동형사상이 존재할 필요충분조건을 알아볼 겁니다. 그럼 시작하겠습니다. 이번에 소개할 정리는 다음과 같다. 이제 증명해 보자. 필요충분조건을 증명하는 것 이므로 다
pilgigo.tistory.com
여기를 참고해 주세요.

여기서

이에 대한 증명은
선형대수학 시리즈 10편(선형독립의 성질 행렬 표현으로 해석)
이번 편은 선형독립의 성질에 대해 알아볼 겁니다. 그럼 시작하겠습니다. 이번에 소개할 정리는 다음과 같다. 이제 증명해 보자. 그러므로이다. 두 번째로 소개할 정리는 다
pilgigo.tistory.com
여기를 참고해 주세요.
그러므로

이다.
그리고

여기서
이에 대한 증명은
선형대수학 시리즈 10편(선형독립의 성질 행렬 표현으로 해석)
이번 편은 선형독립의 성질에 대해 알아볼 겁니다. 그럼 시작하겠습니다. 이번에 소개할 정리는 다음과 같다. 이제 증명해 보자. 그러므로이다. 두 번째로 소개할 정리는 다
pilgigo.tistory.com
여기를 참고해 주세요.
그러므로
이다.
고로
이에 대한 증명은
선형대수학 시리즈 29편(선형변환 합성 행렬표현)
이번 편은 선형변환 합성을 행렬표현으로 계산하는 공식을 알아볼 겁니다. 그럼 시작하겠습니다. 이번에 소개할 정리는 다음과 같다. 이제 증명해 보자. 우선 기저 집합과 행렬표
pilgigo.tistory.com
여기를 참고해 주세요.
다시말해
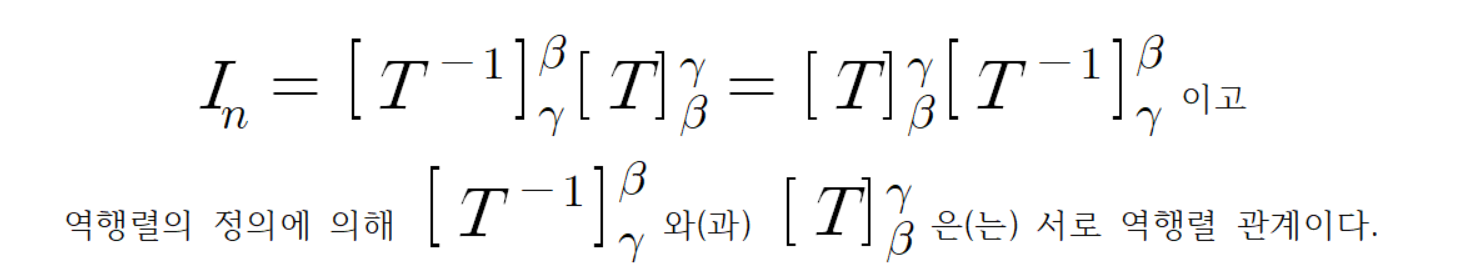
따라서
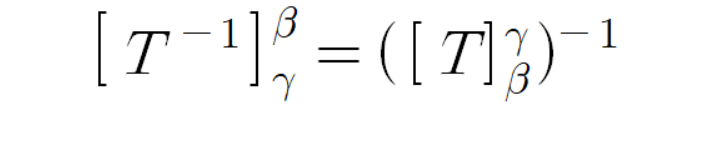
이다.
이를 통해 다음과 같은 결론이 나온다.

T이(가) 선형이면 T의 역함수 또한 선형임에 대한 증명은
선형대수학 시리즈 28편(역사상)
이번 편은 역사상에 대해 알아볼 겁니다. 그럼 시작하겠습니다. 이번에 소개할 정리는 다음과 같다. 이제 증명해 보자.이다.가산성과 동차성을 만족하므로 선형이다.
pilgigo.tistory.com
여기를 참고해 주세요.
첫 번째 명제의 증명이 끝났다.
두 번째 명제를 증명해 보자.

이에 대한 증명은
직사각형 행렬은 역행렬이 있는가?
이번 편은 직사각형 행렬이 역행렬을 가질 수 없음을 증명할 겁니다. 그럼 시작하겠습니다. 이번에 소개할 정리는 다음과 같다.이제 증명해 보자. 역행렬의 정의에 의해하지만 역행렬의
pilgigo.tistory.com
여기를 참고해 주세요.
그러므로
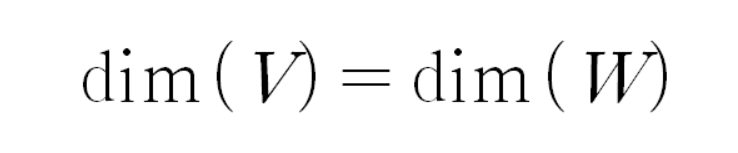
이다.


다음 집합은 공집합이 아니다.
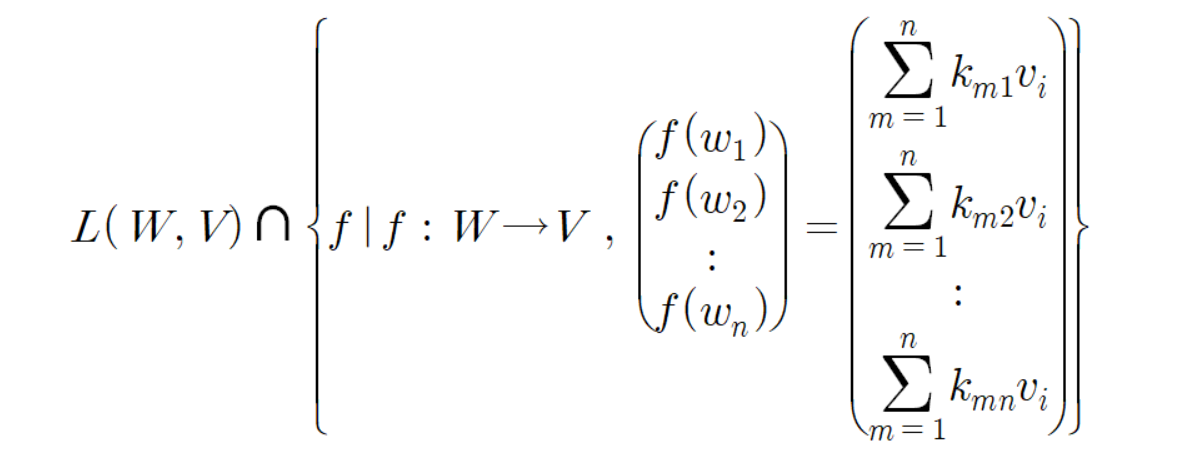
이에 대한 증명은
선형대수학 시리즈 30편(기저와 대응되는 모든 경우에서 선형변환 정의 가능성)
이번 편은 기저와 대응되는 모든 경우에서 선형변환 정의 가능성에 대해 알아볼 겁니다. 그럼 시작하겠습니다. 정리를 소개하기 전 다음과 같은 기호를 정의하자. 이번에 소개할 정
pilgigo.tistory.com
여기를 참고해 주세요.
이를 간단히 표현하면
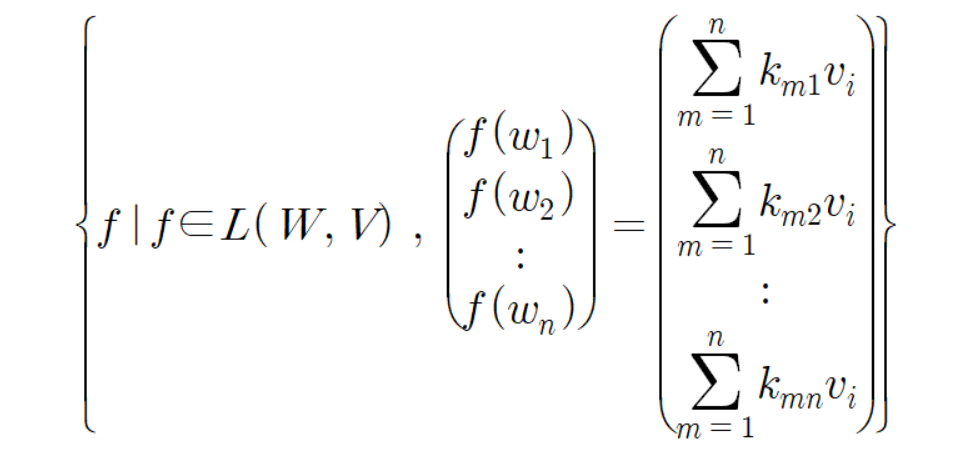
이다.

이다.
고로 선형변환 행렬표현 정의에 의해
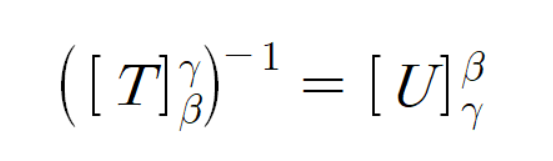
이다.
다시말해

이에 대한 증명은
선형대수학 시리즈 27편(선형변환 합성)
이번 편은 두 선형변환의 합성함수 또한 선형변환인가를 알아볼 겁니다. 그럼 시작하겠습니다. 이번에 소개할 정리는 다음과 같다. 이제 증명해 보자.이다.가산성과 동차성을
pilgigo.tistory.com
여기를 참고해 주세요.
그러므로

고로

두 선형변환이 같아지는 것에 대한 증명은
선형대수학 시리즈 22편(기저와 선형변환 관계)
이번 편은 기저와 선형변환 관계를 알아볼 겁니다. 그럼 시작하겠습니다. 이번에 소개할 정리는 다음과 같다. 필요충분조건을 증명하는 것이므로 다음 두 명제를 증명해야 한다.두
pilgigo.tistory.com
여기를 참고해 주세요.
그리고

이것 역시 증명은
선형대수학 시리즈 22편(기저와 선형변환 관계)
이번 편은 기저와 선형변환 관계를 알아볼 겁니다. 그럼 시작하겠습니다. 이번에 소개할 정리는 다음과 같다. 필요충분조건을 증명하는 것이므로 다음 두 명제를 증명해야 한다.두
pilgigo.tistory.com
여기를 참고해 주세요.
따라서

두 번째 명제의 증명도 끝났다.
첫 번째 명제도 참이고 두 번째 명제도 참 이므로
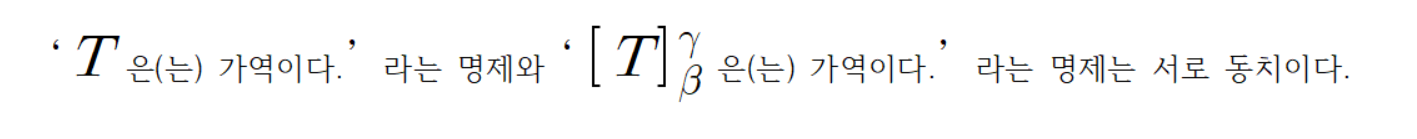
따라서 필요충분조건이 될 수 있다.
'수학' 카테고리의 다른 글
| 공리계의 독립성을 증명하는 방법 (2) | 2024.10.27 |
|---|---|
| 공리계와 여러 성질들 용어 정의(무모순성과 독립성) (0) | 2024.10.26 |
| 선형대수학 시리즈 32편(동형사상이 존재할 필요충분조건) (0) | 2024.10.12 |
| 선형대수학 시리즈 30편(기저와 선형변환 관계 심화버전) (0) | 2024.10.11 |
| 선형대수학 시리즈 29편(선형변환 합성 행렬표현) (0) | 2024.10.07 |